Системы линейных уравнений
Лекция 11
Методы решения систем уравнений установившегося режима
Системы линейных уравнений
Система линейных уравнений установившегося режима формируется при задании нагрузок в узлах в виде постоянного тока Іі = const:
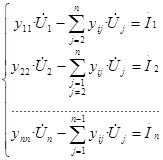; (1)
В матричной форме её можно записать:
,
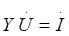где вектор І = Ізд – Yоп Uоп , Ізд – вектор заданных токов в узлах.
Для выполнения преобразований будем использовать общепринятую форму записи СЛАУ:
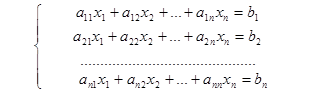(2)
Система уравнений (2) в матричной форме:
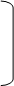
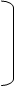
а11 а12 … а1n x1 b1
a21 a22 … a2n x2 = b2 (3)
… … … … …
an1 an2 … ann xn bn
или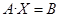 
и соответствует системе уравнений установившегося режима Y*U=I. При этом элементам матрицы коеффициентов А соответствует элементы матрицы проводимостей Y, вектору неизвестных X соответствует вектор напряжений U и вектору свободных членов В соответствует вектор заданных токов I.
Методы решения СЛАУ разделяются на две группы: прямые и итера-ционные.
Прямые(точные) методы позволяют получить точные значения искомо-го решения в результате выполнения конечного числа арифметических опера-ций (метод Гаусса, метод Жордана, метод LU- факторизации, метод двойной факторизации и др.). Используются для решения систем линейных уравнений.
Итерационные(приближенные) методы позволяют получать решение системы уравнений с заданной точностью как результат выполнения опреде-ленного числа итераций (метод Простой итерации, метод Зейделя, метод Ньютона-Рафсона и др.).
Итерационные методы заключаются в многократном повторении единооб-разных вычислений(итераций) с постепенным приближением к искомому ре-зультату. Используются для решения, в основном, систем нелинейных урав-нений.
Решение СЛАУ методом Гаусса
(Метод последовательного исключения неизвестных)
Существует много модификаций метода Гаусса, некоторые из них рас-сматриваются как самостоятельные методы. В основе их лежат эквивалент-ные преобразования системы уравнений к тому или иному виду, как резуль-тат последовательного исключения неизвестных.
Классический метод Гаусса включает 2-а последовательных этапа вычисле-ний – прямой и обратный ход.
1. Прямой ход.
Заключается в преобразовании исходной СЛАУ (2), (3) с прямоугольной мат-рицей коэффициентов к эквивалентной системе с треугольной матрицей ко-эффициентов (системы эквивалентны, если решение одной из них является решением другой).
Прямой ход метода Гаусса состоит в последовательном выполнении одно-типных шагов исключения неизвестных. На первом шаге, преобразования вы-полняются таким образом, чтобы исключить элементы уравнений, содержа-щие неизвестную величину х1, из второго и последующих уравнений. Полу-чаем эквивалентную систему уравнений вида:
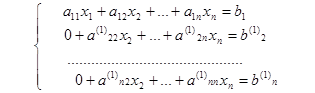
На втором шаге исключаются элементы, содержащие неизвестную х2 из уравнений, начиная с третьего и т.д. В результате выполнения (n-1) шага ис-ключения неизвестных, получаем эквивалентную систему уравнений с треугольной матрицей коэффициентов:
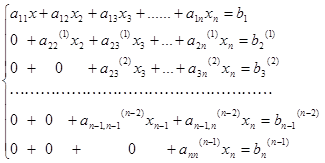
Для выполнения исключения неизвестных на каждом шаге существуют раз-личные варианты эквивалентных преобразований уравнений (умножение или деление их на один и тот же коэффициент, сложение или вычитание уравне-ний и т.д.), в том числе можно использовать формулы:
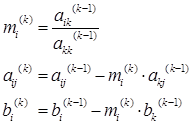Здесь: к- номер шага исключения
к =1,….,n-1;
Соответствует номеру уравнения, которое
будучи умноженным на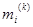 
, вычитается из
остальных уравнений.
i – номер уравнения из которого исключается неизвестная, і = к+1, … , n;
j – номер элемента в уравнении (номер столбца), j = k, … , n.
Диагональные коэффициенты а11, а22(1), а33(2), ..., аnn(n-1) называются ведущи-ми элементами. Они не должны быть равными нулю (условие получения ре-шения). Чем больше эти значения по абсолютной величине, тем точнее будет решение. Достигается это перестановкой уравнений, начиная с (к + 1) – го. Соответствующая модификация метода - метод Гаусса с выбором ведущего элемента.
2. Обратный ход метода Гаусса
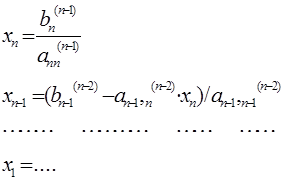Заключается в определении зна-чений неизвестных, начиная с по-
следнего.
Из последнего уравнения преоб-разованной системы находим xn, затем подставляем его в пред-последнее уравнение и находим из него xn-1, и так далее. Из пер- вого уравнения определяем x1.
Для проверки правильности решения - найденные значения подставляем в исходные уравнения. Они должны обратиться в тождества.
Классический метод Гаусса лежит в основе большинства методов и мо-дификаций, объединенных общим названием - методы исключения. Они базируются на последовательном исключении неизвестных из СЛАУ. Применительно к уравнению установившегося режима, такие преобразова-ния соответствуют исключению узлов и их линий связи из расчетной схемы, то есть, если из системы уравнений установившегося режима исключается неизвестная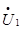 
, то это соответствует исключению первого узла и его линий связи из схемы:
 |
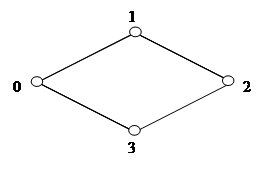
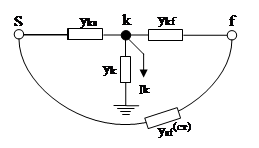
При исключении к- го узла, связанного с узлами s и f , звезда узла к преобразуется в многоугольник:
 | |||
 | |||
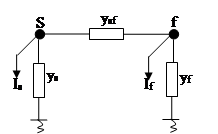Появляется новая линия s-f, её проводимость определяется по формуле:
,
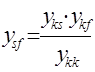где ykk- cобственная проводимость к- го узла.
Если ветвь s-f уже существовала (с проводимостью ysf(ст)), то проводимость новой линии:
.
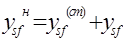Проводимость узла yk и ток Ik разносятся в смежные узлы s и f . Эти величины мы можем определить по формулам:
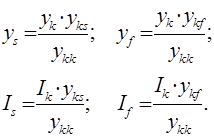
Такое преобразование схемы соответствует к-му шагу исключения неиз-вестных на прямом ходе метода Гаусса и является эквивалентным, т.к. напряжения и токи в остающихся (на данном шаге) ветвях и узлах остаются неизменными.
При выполнении прямого хода метода Гаусса появляются новые ненуле-вые элементы в матрице проводимостей Y. Топологически это соответст-вует образованию новых ветвей при преобразовании многолучевой звезды в многоугольник. Их количество сильно зависит от последовательности рас-смотрения уравнений при выполнении прямого хода.
Пример:
Решение систем линейных уравнений методом Жордана
(Метод Гаусса без обратного хода)
Решение СЛАУ выполняется за один этап, в результате которого мат-рица коэффициентов А преобразуется в единичную матрицу Е:
Ах= В;
Ех= В(n);
x= B(n).
Выполняется n последовательных шагов исключения неизвестных.
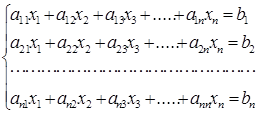
На первом шаге первое уравнение делим на ведущий элемент а11 и ис-ключаем неизвестную х1 из всех уравнений начиная со второго (аналогично методу Гаусса):
А(1)х=В(1)
Получаем систему уравнений в виде:
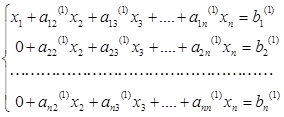
На втором шаге исключения второе уравнение делится на а22(1) и неиз-вестная х2 исключается из всех уравнений, исключая второе уравнение:
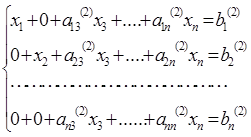
На к-ом шаге исключения к-ое уравнение делится на коэффициент акк(к-1) при xk и неизвестная хк исключается из всех уравнений, кроме к-го.
Формулы для пересчета коэффициентов aij аналогичны формулам метода Гаусса, но отличаются пределами изменения индекса i: i=1,…,n; i≠k.
В результате выполнения n шагов, исключения неизвестных получаем эквивалентную систему уравнений, в которой матрица коэффициентов равна единичной:
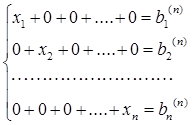
Ех= В(n); x= B(n).
В ней правые части уравнений - искомые значения неизвестных х, то- есть они являются решением исходной системы уравнений.
Возможны модификации этого метода с выбором ведущего элемента.
Дата добавления: 2016-01-26; просмотров: 502;