Функциональный подход

В этом разделе мы попытаемся ответить на вопрос: для чего существуют органы. Заметим, что в физике вопросы такого рода не задаются. Иное дело техника. Когда мы строим дом, машину, дорогу и т. д., мы всегда руководствуемся определенной целью, т. е. мы прекрасно знаем, для чего работаем.

В нашей трудовой деятельности все рационально, мы хотим достигнуть желанной цели с минимальными затратами. Ведь смешно же стрелять из пушек по воробьям. Сам процесс труда обычно удовольствия не доставляет, для человека гораздо важнее цель. Вот что сказал по этому поводу Ф.М. Достоевский: «Мне пришло раз на мысль, что если б захотели вполне раздавить, уничтожить человека, наказать его самым ужасным наказанием, так что самый страшный убийца содрогнулся бы от этого наказания и пугался его заранее, то стоило бы только придать работе характер совершенной, полнейшей бесполезности и бессмыслицы».

Для уменьшения энергетических затрат человек создает орудия: сначала дубину и каменный топор, а потом и машины. Сотни тысяч лет орудийной деятельности, естественно, наложили отпечаток на наши мышление и язык. Глаза нам нужны, чтобы видеть, уши – чтобы слышать, руки – чтобы работать, т. е. все органы являются лишь средством для удовлетворения наших желаний. Домашние животные человеку также даны для удовлетворения потребности в пище, для переноса тяжестей и т. д. Более того, той же цели могла бы служить и вся природа. Но, увы, приспособить природу удается далеко не всегда, поэтому для завершения картины мира, где все подчинено целям, надо было придумать богов – носителей целей более высокого порядка, для достижения которых и люди, и все объекты природы выступают как орудия.

Поняв это, мы должны были бы отказаться не только отвечать на вопросы «для чего» и «ради чего», но даже и ставить эти вопросы. Более того, следовало бы признать ненаучным и сам термин «функция». Однако немного подумав, мы поймем, что это странное целевое мышление помогает человеку эффективнее организовать свою деятельность для удовлетворения своих насущных потребностей, в конечном счете такое мышление способствует увеличению числа потомков. Но разве не те же потребности испытывают особи любого вида?

Тут мы подходим к очень важному пункту нашего рассуждения – сущности живого. По‑видимому, главное свойство жизни – это ее принадлежность к открытым термодинамическим системам, находящимся вдали от равновесия. Длительное существование таких систем возможно только за счет постоянного притока извне энергии и вещества. Внутри живой системы идут постоянные процессы старения (повышения ее энтропии), но от гибели ее удерживают процессы омоложения (производства отрицательной энтропии). Иначе говоря, для длительного существования популяции ее особи вынуждены все время питаться и стареть, компенсируя последнее постоянным производством потомства. Кроме того, учитывая смертность не только по причине старения, но и по другим (изменение физикохимических условий среды, хищничество, паразитизм и т. д.), производство потомства должно компенсировать все варианты гибели особей.

Теперь приглядимся к тому, что человек делает, когда работает. Возьмем, к примеру, тяжелый труд земледельца. Человек очищает поле от леса, взрыхляет почву, помещает в нее семена злаков, борется с сорняками и пр. Наконец, жнет, молотит, перетирает зерно и печет хлеб. Сколько труда он затратил! Крестьянину кажется, что он выращивал хлеб, а на самом деле хлеб вырастал сам. Да и не в силах хлебопашец осуществить химический синтез углеводов из углекислоты и воды. Это делается самим растением, использующим в качестве источника энергии солнечные лучи. Человек же только создает условия для роста нужного злака. Работая в течение примерно ста дней в году «в поте лица своего», он при самой примитивной технике в состоянии обработать около трех гектаров пашни и получить с них около двух тонн зерна, что более чем достаточно для жизни его семьи в течение года.

Таким образом, работа земледельца фактически сводится к отведению части лучистой энергии Солнца к биомассе людей. Однако сам крестьянин ставит перед собой куда более прозаичную цель. Он трудится, чтобы обеспечить себя и свою семью пищей еще на один год. Отметим, что для выживания ему нужно трудиться и обладать знаниями по выращиванию хлеба.

Теперь перейдем к рассмотрению абстрактной живой системы. С биологической точки зрения, главное заключается в преобразовании поглощенной энергии и вещества в биомассу потомства, ибо только это дает популяции возможность существовать неопределенно долго. В чем заключается материальная основа этого чуда? Что заставляет вещество из окружающей среды постоянно превращаться в биомассу популяции? Уж не жизненная ли сила?

Рассмотрим какое‑нибудь элементарное событие в этом потоке энергии и вещества. Ну, скажем, этап распада поглощенных углеводов. Суммарное уравнение, описывающее окисление глюкозы, выглядит очень просто:

глюкоза + 6O₂ → 6СО₂ + 6Н₂О + 680 ккал.

Эта реакция может идти и сама по себе без всякого участия живых организмов. Например, нагрев сухую глюкозу, мы можем ее сжечь, т. е. точно так же превратить в CO₂ и Н₂O, но в этом случае вся разность свободных энергий углевода и продуктов его сгорания практически моментально рассеется в форме тепла, не совершив никакой полезной работы. У живых организмов эта энергия освобождается поэтапно, аккумулируясь в специальных химических соединениях (чаще всего это АТФ). Каждая грамм‑молекула АТФ запасает около 7,3 ккал, которые затем могут быть использованы для совершения различных видов работы. Поэтому биологический смысл приведенной выше реакции состоит в преобразовании химической энергии глюкозы в энергию нескольких молекул АТФ:

глюкоза + 6O₂ + 36 АДФ → 6СО₂ + 36 АТФ + 42Н₂O.

Сравнив эту реакцию с предыдущей, мы видим, что живой системе удается использовать только 263 ккал (7,3 ккал х 36) из 680 возможных, т. е. эффективность использования энергии составляет 39 %, остальные 61 % безвозвратно теряются в виде тепла. Нематериальная жизненная сила могла бы иметь к.п.д. и повыше.

Рассматривая любой биохимический процесс распада, мы всегда встречаемся с одной и той же ситуацией: запас свободной энергии у реагирующих компонентов выше, чем у конечных продуктов. Это является индикатором необратимости процесса, самопроизвольности его протекания, хотя ничего не сообщает о его скорости. Но именно скорость имеет в данном случае принципиальное значение. Выходит, мудрое изречение «под лежачий камень вода не течет» отражает глубокую истину. Ведь, собственно говоря, как это вода не течет под камень? С научной точки зрения, вполне течет, только очень медленно. Чтобы потекла быстро, камень надо слегка пошевелить, т. е., приложив усилия, совершить работу. Мешок с глюкозой можно хранить годами и, несмотря на свободный доступ кислорода, процесс окисления сахара идет крайне медленно. Оказывается, для запуска любой химической реакции реагенты должны преодолеть некоторый энергетический барьер (иной раз довольно существенный). Химик решает эту проблему, нагревая реакционную смесь или внося в нее катализатор.

Живые организмы идут по второму пути. Биохимические реакции ускоряются с помощью специальных катализаторов – ферментов – белков, способных образовывать специфичные комплексы с молекулами реагентов. Ферменты не вносят в систему энергию, а только снижают активационные барьеры реакций. Как это происходит – предмет специальной науки – молекулярной энзимологии. Однако ясно одно, ничего сверхтаинственного здесь нет. Энергия, необходимая для изменения пространственной конфигурации реагирующих молекул, освобождается при образовании специфичного комплекса с ферментом.

Каталитические свойства фермента всецело обусловлены строением его молекулы, которое, в свою очередь, полностью определяется последовательностью нуклеотидов ДНК соответствующего гена. Следовательно, в данном случае продукт гена способен ускорять протекание вполне определенной химической реакции. Выражаясь более антропоморфно, можно сказать, что организм, располагая таким геном, обладает «знанием» о том, как осуществить совершенно конкретную химическую реакцию. Это знание, очевидно, заключено в последовательности нуклеотидов генного локуса. Чтобы знание подобного рода «сработало», нуклеотидная последовательность гена должна быть преобразована в аминокислотную последовательность белка, размноженную в гигантском числе экземпляров, т. е. на синтез молекул фермента нужно затратить немало энергии и вещества. Итак, живая система, с одной стороны, должна обладать информацией о строении белка, а с другой – затратить энергию на его синтез и при этом, очевидно, остаться в выигрыше.

Синтез макромолекул сам собой не идет. Для его осуществления мало располагать ферментами, нужна еще и энергия. Самопроизвольное протекание реакции синтеза можно обеспечить ее сопряжением с реакцией распада, наподобие рассмотренной выше. Нужно, чтобы свободная энергия исходных реагентов обеих реакций – сопрягающей и сопрягаемой – была выше свободной энергии их продуктов. Опыт биохимии свидетельствует, что этот энергетический закон выполняется во всех без исключения случаях. Получается, что жизнь как явление вполне подчиняется законам химической термодинамики. Это отражено в одном из определений жизни, данном Ж. Перре: «Жизнь есть потенциально способная к самовоспроизведению открытая система сопряженных химических реакций, катализируемых последовательно и почти изотермично сложными и специфичными органическими катализаторами, которые сами вырабатываются этой системой».

Итак, все макромолекулы организма (в том числе и все ферменты) синтезируются за счет энергии, поступающей из внешней среды. Для животных источником этой энергии обычно служат белки, жиры и углеводы других организмов. Для растений таким источником является Солнце. В этом отношении все живые системы равны, их различия касаются только их динамических характеристик и прежде всего скорости синтеза биомассы.

Функции

Прямой анализ нуклеотидных последовательностей ДНК выявил принципы внутреннего устройства генов. Оказалось, что огромное большинство генов кодирует аминокислотные последовательности белков, обладающих в принципе безграничными возможностями молекулярного узнавания. В одном случае это ферменты, узнающие молекулы субстрата и снижающие активационные барьеры соответствующих химических реакций; в другом – так называемые структурные белки, занимающие свои совершенно определенные места в каких‑то мультимолекулярных ансамблях; в третьем – белки‑регуляторы, узнающие определенные последовательности ДНК. Во всех случаях нуклеотидная последовательность, кодирующая первичную структуру белка, фактически определяет его функцию.

Будем считать, что структура обладает функцией, если она обеспечивает протекание любого процесса, способствующего преобразованию энергии окружающей среды в биомассу популяции. Такие структуры будем называть рабочими. Оказалось, что все молекулярные структуры, закодированные в генах, обладают какой‑то функцией. Более того, большинство этих функций настолько важны, что удаление гена очень часто вызывает остановку развития организма.

Теперь попробуем разобраться с предназначением видимых глазом морфологических структур. Возьмем, к примеру, такую структуру, как зубы позвоночного. Их очевидная функция состоит в том, чтобы питательное вещество, заключенное в относительно крупной жертве, быстрее обработать ферментами пищеварительного тракта. Тонкое измельчение пищевого куска повышает на порядки скорость его переваривания. Ну, а если размер пищевого куска больше самого хищника, то без зубов и челюстей вообще не обойтись. Получается, что челюсти с зубами выполняют функцию, сходную с пищеварительными ферментами: и те, и другие ускоряют процесс первичной обработки пищи. Челюсти действуют здесь как катализатор дезинтеграции тела жертвы. Для этого требуется энергия, которая идет на механическую работу измельчения, а также на создание и поддержание соответствующих рабочих структур.

Вообще, для поддержания жизни должен быть выполнен целый ряд объективно необходимых условий. Процесс питания включает в себя несколько стадий, неумолимых в своей последовательности. Особь должна встретиться с источником пищи (обычно это особь другого вида), измельчить ее, химически расщепить макромолекулы жертвы до униформных блоков и, наконец, доставить данные блоки каждой своей клетке. Заметим, что вся эта сложная цепь оборвется, если нарушится хотя бы одно ее звено.

Само собой разумеется, что для существования организма должно постоянно выполняться условие его охраны от негативных внешних факторов, зачастую весьма агрессивных. Это достигается с помощью панцирей, шипов, средств оптической маскировки, иммунной защиты и т. д. Среда, в которой существует живая система, изменчива, флуктуируют все ее параметры: температура, влажность, соленость и т. д. Все это могло бы нарушить течение многих жизненно важных процессов. Поэтому организм должен обладать способностью сохранять значения своих внутренних параметров при флуктуациях среды, иными словами, он должен обладать системой внутреннего гомеостаза.

Кроме того, особь может погибнуть, что называется, во цвете лет просто случайно (от удара молнии, пожара, потопа, кирпича, упавшего с крыши, и т. д.). Есть только одно средство скомпенсировать ущерб от всех этих напастей – особи популяции должны постоянно воспроизводиться. Но это тоже не очень‑то просто: ведь необходимо произвести половые клетки (гаметы), обеспечить их слияние и защитить от внешней среды первые стадии онтогенеза.

Итак, для неопределенно долгого (стационарного) существования живой системы необходимо, чтобы: 1) извне в нее постоянно поступали энергия и вещество, 2) из нее во внешнюю среду постоянно удалялись тепло и отработанные продукты, 3) особи охранялись от преждевременной гибели, 4) внутренние параметры системы были стабильными, 5) шло постоянное производство новых особей.

Перечисленными свойствами должны обладать любые многоклеточные организмы, иначе говоря, все они должны обладать пятью основными функциями: доставки, удаления, охраны, гомеостаза и воспроизведения.

Если исследовать все многообразие взаимодействий между организмом и средой, а также между различными частями одного организма, то нам откроется бесчетное число функций, подчиненных основным. Возьмем, к примеру, кости конечностей позвоночных. Мы найдем здесь и поверхности суставов, и отростки для прикрепления мышц, и отверстия для нервов и сосудов, т. е. морфологические признаки, имеющие четкую функциональную нагрузку. Распилив кость, обнаружим, что костные балки располагаются вдоль линий сжатий и растяжений, в полном соответствии с теорией сопротивления материалов. Кроме того, в полостях трубчатых костей млекопитающих мы найдем кроветворную ткань – костный мозг. А у птиц эти полости заполнены воздухом и связаны с легочными мешками; получается двойной функциональный эффект – масса тела уменьшается, а дыхание интенсифицируется.

Подобный анализ можно продолжать бесконечно, и всюду мы будем находить функциональное назначение морфологических структур. Этот поиск и обнаружение целесообразности в строении живых организмов настолько завораживают, что возникает невольная мысль о целесообразности их малейших черточек. Такая точка зрения, безусловно, относится к ненаучным, так как в реальном мире нет места для идеальных объектов. Совершенно ясно, что доведенная до предела целесообразность автоматически требует признания существования бога.

Обобщив результаты нашего функционального анализа, можно прийти к заключению, что живое вещество фактически является лишь средством для жизни как процесса, состоящего в производстве этого же вещества, т. е. цель и средство здесь удивительным образом переплетены. Получается, что для потребления энергии из окружающей среды живая система должна обладать большим набором функций и постоянно затрачивать энергию на синтез соответствующих рабочих структур. Вообще, живое вещество можно рассматривать как единый катализатор, способный сам себя синтезировать в процессе катализируемой реакции. Ясно, что масса живого вещества будет расти в геометрической прогрессии, и в той же прогрессии будет нарастать энергетический поток внутрь живой системы. Предел этому может положить только ограниченность ресурсов внешней среды.

Итак, любая живая система (будь то людское общество или природная популяция) для продления своего существования должна постоянно потреблять из окружающей среды энергию и вещество. Большая часть этого потока растрачивается на тепло и отбросы, а остальная идет на создание и поддержание рабочих структур, сохраняющих мощность энергетического потока вовнутрь системы на прежнем уровне.

Каждая такая структура выполняет свой, специфичный для нее вид работы. Мерой функциональной эффективности структуры может служить ее мощность, т. е. объем работы, выполняемой за единицу времени в режиме максимальной нагрузки. Нередко структура является необходимой, но инертной частью какого‑нибудь сложного аппарата (например, локомоторного), или же ее функциональное назначение связано с пассивной защитой (например, панцирь с шипами). В этом случае строение структуры должно соответствовать максимальной нагрузке со стороны каких‑то активных внешних или внутренних факторов. Способность уравновешивать подобные нагрузки также можно назвать мощностью. Это позволяет говорить о мощном костяке, мощных крыльях, мощном панцире и т. д.

Достаточно беглого взгляда на рис. 4, Б, чтобы сказать, что по мощности легких млекопитающие значительно превосходят земноводных. Выходит, что из анализа строения ряда гомологичных структур мы можем извлечь информацию об их функциональном назначении и мощности. В целом же все рабочие структуры – от молекулярных до морфологических – можно считать информационными. Выражаясь более антропоморфно, любая живая система обладает «знанием» об условиях преобразования энергии и вещества внешнего мира в собственную биомассу.

Аллометрия

Родственные виды животных обычно различаются средними размерами своих особей. Кроме того, типичные особи могут различаться по многим количественным характеристикам (параметрам), таким как величина любого органа, потребление кислорода, число митохондрий в клетке печени, средняя продолжительность жизни и многое другое. Оказалось, что для совокупности видов одного таксона величины подобных параметров (X ) очень часто связаны с массой особи (М) так называемой аллометрической зависимостью

X = а*М^α , (2.2)

где а и α – аллометрические коэффициенты.

Заметим, что зависимости такого рода связывают две характеристики типичной особи каждого вида в пределах всей таксономической группы.

Известно, что при увеличении размеров шара его объем возрастает пропорционально кубу, а поверхность – только квадрату радиуса. Этот же закон обычно выполняется и при пропорциональном (изометричном) увеличении тел более сложной формы: длины всех одномерных структур возрастают пропорционально кубическому корню из массы тела, т. е. пропорционально М^0,33 , а площади всех поверхностей – пропорционально М^0,67.

Выберем в качестве параметра одну из важнейших характеристик особи – скорость потребления ею энергии в состоянии покоя, т. е. мощность основного метаболизма (обмена веществ). Этот параметр можно оценить либо по скорости потребления кислорода, либо по скорости рассеивания тепла. Естественно, при увеличении размеров особи растет и мощность ее метаболизма (Р). Эта связь выражается эмпирическим уравнением

Р = а*М ^0,75. (2.3)

Здесь коэффициент а численно равен мощности основного метаболизма особи с единичной массой (скажем, с массой 1 кг). После логарифмирования уравнение (2.3) приобретает вид

ln Р = ln а + 0,75 ln М. (2.4)

Значит, в логарифмическом масштабе мы должны иметь линейную связь между мощностью метаболизма особи и массой ее тела. Если эту связь представить графически, то все плацентарные млекопитающие (от мыши до слона) и птицы (кроме воробьиных) попадут на одну прямую, наклон которой равен 0,75 (рис. 6). Все эти животные имеют очень близкие значения коэффициента а. Для сумчатых, плацентарных млекопитающих и воробьиных птиц данный коэффициент равен соответственно 46,5; 73,3 и 129,0. Для амфибий и рептилий его значения колеблются в диапазоне от 0,8 до 7,8. Получается, что особи одной массы, но принадлежащие к разным таксонам, рассеивают в состоянии покоя разное количество энергии.

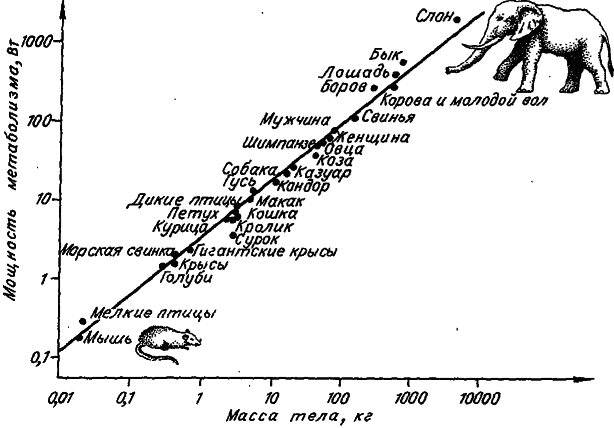
Рис. 6. Кривая «от мыши до слона». Зависимость мощности метаболизма от массы у млекопитающих и птиц (по: [Benedict, 1938]).

Разделив обе части уравнения (2.3) на М , получим связь массы тела со скоростью рассеивания энергии единицей массы животного, т. е. с удельной мощностью метаболизма (р):

р = а*М^‑0,25 . (2.5)

Знак минус при показателе степени свидетельствует о том, что с ростом массы особи удельная мощность метаболизма падает. Эта закономерность верна для всех животных, объединенных общим значением коэффициента а. Заметим, что у млекопитающих размеры гомологичных клеток отличаются незначительно, поэтому уравнение (2.5) указывает на ослабление метаболизма средней клетки при увеличении массы животного.

Жизнь особи многообразна. Животное может и мирно отдыхать, и мчаться изо всех сил, спасаясь от смертельной опасности или преследуя свою жертву. Совершенно ясно, что в течение своей жизни организм неоднократно испытывает максимальные физические нагрузки. Главные энергетические расходы животных, безусловно, связаны с активным движением. Достаточно отметить, что при интенсивных мышечных усилиях потребление кислорода возрастает в 10–30 раз. Поэтому мы должны прежде всего рассмотреть, как изменяется режим работы мышц при увеличении размеров особи.

Как известно из механики, работа (A) равна произведению силы на путь. При сокращении мышцы на длину Δl она совершает работу в соответствии с формулой

А = S*σ*Δl , (2.6)

где S – площадь поперечного сечения мышцы; σ – сила, развиваемая мышечным пучком единичного сечения.

Обширный экспериментальный материал свидетельствует, что у всех животных величина σ очень близка. Это объясняется универсальностью строения элементарного мышечного волокна (миофибриллы) и тождественностью молекулярного механизма его сокращения. Поскольку гомологичные мышцы в среднем укорачиваются на одну и ту же долю (примерно на 30 %), то чем мышца длиннее, тем на большую длину она сокращается. Следовательно, работа, совершаемая мышцей при сокращении, пропорциональна ее сечению и длине, т. е. пропорциональна ее объему (или массе).

Теперь посмотрим, как все это отражается на двигательной активности животного и прежде всего на его беге. Бег состоит из последовательности циклов сокращения и расслабления практически всех скелетных мышц. При каждом таком цикле животное перемещается на один шаг, совершая работу, пропорциональную массе своей мускулатуры. А так как эта последняя у млекопитающих составляет в среднем около 40 % от массы тела, то получается, что работа по перемещению на один шаг пропорциональна массе животного, т. е.

А_ш~ М . (2.7)

Очевидно, что чем длиннее ноги у животного, тем больше его шаги, т. е. тем меньше нужно их сделать для преодоления одной и той же дистанции. Как показывают измерения, у млекопитающих разных видов длина ног пропорциональна M^0,33 . Значит, число шагов (n), нужное для покрытия фиксированного расстояния, скажем, один километр, должно быть связано с массой тела соотношением

n ~ М^‑0,33 . (2.8)

При этом животное совершает работу A, равную nA_ш, т. е., учитывая (2.7) и (2.8),

A ~ М^0,67 . (2.9)

Поделив обе половины этого соотношения на М, получим, что работа по транспорту единицы массы тела на фиксированное расстояние (A₀) должна уменьшаться при укрупнении животного, точно отражая сокращение необходимого числа шагов:

А₀ ~ М^‑0,33. (2.10)

Объем работы А₀ можно оценить по количеству кислорода, необходимому для переноса килограмма массы тела на один километр. Оказалось, что эта величина ц – кислородная цена транспорта единицы массы – падает с увеличением размеров животного, подчиняясь аллометрическому уравнению

ц = c*M^‑0,33 . (2.11)

Ясно, что кислородная цена транспорта всей массы животного на один километр (Ц ) будет в М раз больше, т. е.

Ц = с*М^0,67 . (2.12)

Самая поразительная особенность этого уравнения заключается в том, что оно справедливо для всех бегающих наземных животных – ящериц, млекопитающих и даже насекомых. Значение коэффициента с изменяется у разных групп очень незначительно – от 0,6 до 0,8 литра кислорода для перемещения одного килограмма на один километр. Фактически это означает, что эффективность локомоторного аппарата у всех наземных животных примерно одна и та же, вне зависимости от их эволюционной продвинутости. Скорее всего это постоянство зиждется на единстве строения миофибриллы – основной рабочей структуры любой скелетной мышцы.

Теперь посмотрим, как связана с массой тела мощность, развиваемая животным при беге. Напомним, что мощность – это работа, совершаемая за единицу времени. Заменив в уравнении (2.6) величину Δl на абсолютную скорость укорочения мышцы v, мы получим формулу для оценки мощности мышечного сокращения (P_m ):

P_m = S*σ*v. (2.13)

Поскольку максимальные значения v для мышц разных видов животных (при одной температуре) близки, то максимальная мощность мышцы определяется площадью ее поперечного сечения S. Эта площадь при изометричном росте должна увеличиваться пропорционально М^0,67 , и точно так же должна возрастать мощность мышечного сокращения. Но, как мы знаем (см. уравнение (2.3)), мощность метаболизма увеличивается с ростом массы существенно быстрее. Для метаболизма покоя показатель степени при массе равен 0,75, а при нагрузках он достигает у млекопитающих даже 0,81.

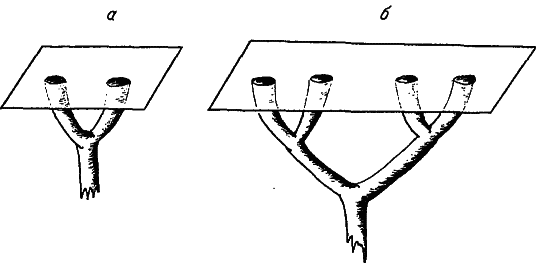
Рис. 7. Усложнение ветвления одномерных структур при увеличении размеров органов.

а – простая структура; б – сложная.

По‑видимому, некоторое превышение реальной мощности метаболизма над уровнем, достаточным для снабжения энергией скелетной мускулатуры, ведет к ускорению бега животного. Скорость бега можно определить, перемножив частоту шагов на длину среднего шага. Измерения показали, что с увеличением размеров животных частота их шагов снижается существенно медленнее, чем возрастает длина шага, в итоге бег ускоряется.

Итак, увеличенные размеры дают определенные преимущества. Во‑первых, без снижения скорости (и даже при ее некотором росте) бег становится более экономичным. Во‑вторых, падает удельная мощность метаболизма, что фактически означает уменьшение энергетических расходов на поддержание жизни единицы биомассы. Однако эти, казалось бы, явные плюсы сменяются на минусы при беге в гору. Для поднятия единицы массы тела на одну и ту же высоту животным вне зависимости от их размеров нужно затратить одно и то же количество энергии, но удельная мощность метаболизма у мелких животных больше, поэтому при беге в гору им надо повысить эту мощность в меньшее число раз, чем крупным животным. Так, при беге по вертикали мышь увеличивает потребление кислорода на 20 %, а лошадь – на 630 %. Значит, бегать по пересеченной местности мелким животным легче.

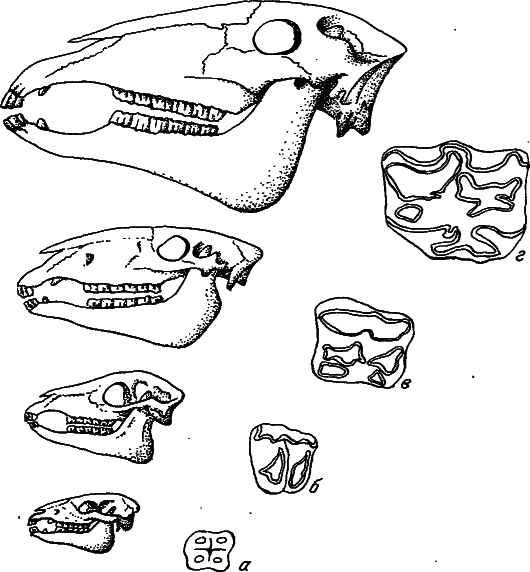
Рис. 8. Усложнение поверхности зубов у лошадей в процессе эволюции (по: [Хадорн, Венер, 1989]).

а – Eohippus (эоцен); б – Mesohippus (олигоцен); в – Merychippus (миоцен); г – Equus (плиоцен – современность).

Время жизни особи принято измерять годами, днями и т. д., хотя его можно было бы отсчитывать и числом каких‑нибудь внутренних циклов – числом сердцебиений, дыхательных движений, опорожнений кишечника, делений клеток определенного типа и т. д. На выполнение каждого такого цикла требуется энергия, в связи с этим поток энергии, приходящийся на единицу массы тела (т. е. удельную мощность метаболизма р ), можно выбрать в качестве меры скорости протекания всевозможных циклических процессов. Чем эта скорость выше, тем больше циклов совершается в организме за единицу астрономического времени, т. е. тем быстрее течет собственное время индивида. Темп жизни животного ускоряется с уменьшением его массы (см. (2.5)). Это означает, что мелкие животные способны реагировать на изменение окружающей среды быстрее, чем крупные. Обратная сторона медали заключается в ослаблении устойчивости к энергетическому голоду. Хорошо известно, что для крошечных землероек прекращение питания даже на 7–9 часов равносильно гибели.

Попробуем выяснить, как соотносятся между собой размеры тела и рассмотренная выше сложность морфологических структур. Сначала отметим, что увеличение органа может привести к усложнению одномерных структур, обеспечивающих связь этого органа с другими частями организма. На рис. 7 изображено, как повышается ранг ветвления сосудов, протоков, нервов и т. д.

Кроме того, есть веские основания считать, что изометрический рост ведет к непропорциональному увеличению функциональной нагрузки на многие органы. Мы уже отмечали, что при укрупнении животных их суммарный метаболизм возрастает по меньшей мере пропорционально М^0,75 . Однако при изометричном росте площади двухмерных структур увеличиваются существенно медленнее, следуя за М^0,67 . Если эти площади прямо отражают мощности соответствующих структур, то пропорциональный рост приведет к их относительному ослаблению. Отсюда следует, что функционально важные поверхности должны расти быстрее, чем М^0,67, т. е. аллометрично.

В качестве примера посмотрим, как увеличение размеров животного может отразиться на строении зубов. Пусть в эволюции каких‑нибудь травоядных идет увеличение размеров тела, но характер пищи при этом не изменяется. Ясно, что количество пищи, потребляемое особью за сутки, должно соответствовать количеству поглощенного кислорода, т. е. способность перетирать пищу должна соответствовать мощности метаболизма. Поэтому при увеличении массы особи рабочая поверхность зубов должна расти быстрее, чем поверхность тела. Данное требование удовлетворяется за счет появления на перетирающей поверхности зубов характерных выпячиваний – эмалиевых складок и бугорков. Тенденция к усложнению поверхности зубов при увеличении размеров животных хорошо прослеживается в эволюционных рядах лошадей и других травоядных (рис. 8).