Теорема. (Критерий факториальности)
Если кольцо имеет разложение на простые множители, то оно факториально тогда и только тогда, когда для любого простого элемента p из того, что p\(ab) следует, что p\a или p\b.
Критерий кажется очевидным и даже несколько наивным. Однако, если Петю (p) смогли поднять вдвоем Антон (a) и Борис (b) не обязательно, что это они смогут сделать по отдельности.
Теорема (факториальность евклидовых колец).
Любое евклидово кольцо, в частности кольцо целых чисел и кольцо многочленов над полем, являются кольцам с однозначным разложением на простые множители.
Доказательство.
Применим критерий факториальности. Пусть простой элемент p делит произведение ab, но не делит элемент a. Так как элемент p простой, то НОД(p,a) = 1 и, значит, в силу алгоритма Эвклида найдутся элементы 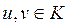 такие, что ua+vp=1. Умножая это равенство почленно на элемент b, получаем uab+vpb=b. Так как оба слагаемых в левой части равенства делятся на элемент p, то и правая часть делится на p. Значит p\b. Если элемент p не делит b, то аналогично получим, что p\a.
такие, что ua+vp=1. Умножая это равенство почленно на элемент b, получаем uab+vpb=b. Так как оба слагаемых в левой части равенства делятся на элемент p, то и правая часть делится на p. Значит p\b. Если элемент p не делит b, то аналогично получим, что p\a.
□
Следствие. В евклидовом кольце число простых элементов бесконечно. В частности, бесконечно число простых чисел и неприводимых многочленов.
Идея использовать метод Евклида для получения новых простых чисел не безнадежна, но мало эффективна. Начнем с первых трех простых чисел 2, 3, 5. Далее получаем 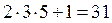 , имея четыре числа 2, 3, 5, 31 получим
, имея четыре числа 2, 3, 5, 31 получим 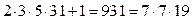 . Вновь появляющиеся числа не только не обязаны быть простыми, но даже и не обязательно дают простые множители, превосходящие предыдущие.
. Вновь появляющиеся числа не только не обязаны быть простыми, но даже и не обязательно дают простые множители, превосходящие предыдущие.
Дата добавления: 2015-11-28; просмотров: 2840;
