Основная теорема арифметики.

Название это несколько устарело, но сама теорема об однозначном разложении на простые множители не устарела. Теорема эта несколько суховата и аккуратно ее сформулировать не так-то просто. Но на ней, как на фундаменте держится вся арифметика, и все приложения теории чисел. Эта же теорема имеет место и для кольца многочленов над полем, а более широко для всех евклидовых колец. Для них мы ее и докажем.

Однозначность далеко не всегда имеет место. Например, игрушку Лего как не разбирай, простейшие детали окажутся одни и те же. А вот огурец можно разрезать вдоль, а можно и поперек.

Что понимать под однозначностью разложения на простые множители. Например, число 10 можно записать разными способами в виде произведения

.

Можно предложить и другие. Однако, различия в этих представлениях не очень существенные. Минус единица и единица, это единственные обратимые элементы в кольце целых чисел (на обратимые элементы делятся любые элементы), а числа 2 и -2, 5 и -5 – ассоциированные, т.е. отличаются друг от друга на обратимые. То, что 2 и 5 в разных записях числа 10 переставлены местами тоже не существенно, поскольку имеем место коммутативность умножения. Все эти наблюдения подсказывают определение.

Определение. Два разложения элемента “a” коммутативного кольца К на простые множители

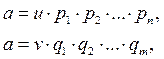
называются ассоциированными, если 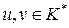- обратимые элементы, n=m, простые элементы p_i и q_j, возможно после перестановки, попарно ассоциированы, т.е. p₁ ассоциирован с q₁, p₂ ассоциирован с q₂ и т.д.

В кольце многочленов простые элементы обычно называют неприводимыми многочленами. Так сложилось исторически, поскольку в прежние времена, разложение многочленов на множители называлось приведением к простому виду. Поэтому, если разложить не удавалось, то и называли неприводимым. Это примерно то же самое, почему у моряков не повар, а кок. Поскольку говорить, что неприводимые элемент кольца многочленов – это простой элемент кольца многочленов, излишний педантизм, то приведем и явное определение.

Определение. Многочлен называется неприводимым, если он не раскладывается в произведение многочленов меньшей степени.

Поиск простых элементов, в том числе и простых чисел и неприводимых многочленов, весьма нетривиальная задача, над которой в мире работают тысячи специалистов и миллионы микропроцессоров. Нам нужно доказать, что в кольце целых чисел Z и кольце P[x] многочленов над полем имеет место однозначное разложение на простые множители. Кстати, на этом факте держится вся криптография с открытым ключом, в том числе и знаменитый RSA.

Как обычно, сделаем это сразу для всех евклидовых колец.

Определение. Говорят, что кольца К является кольцом с однозначным разложением на простые множители, если в нем любой элемент имеет хотя бы одно разложение на простые множители и любые два такие разложения ассоциированы.

Кратко такие кольца называются факториальными. Но можно это слово и не запоминать. Некоторые племена Африки не знают слова зонтик, они просто говорят: “Домик, который белый человек носит в руках и раскрывает над головой, когда идет дождь.”

Фраза в определении факториального кольца о том, что каждый элемент должен иметь хотя бы одно разложение, не ритуальная. Не факт, что такие разложения есть вообще, а про то, чего нет можно доказать все что угодно. Например, я утверждаю, что все алмазы, хранящиеся у меня в доме, имеют вес больше 10 кг. (50 тыс. карат). Что бы меня опровергнуть требуется найти хотя бы один алмаз, который бы весил меньше 10 кг. Такого алмаза найти невозможно потому, что алмазов у меня нет вообще!

Теорема.

В евклидовом кольце любой элемент имеет разложение на простые множители.

Доказательство.

Идея доказательства очень проста. Поскольку каждый элемент евклидова кольца имеет степень, а степень сомножителя не больше чем степень произведения, то мы не сможем бесконечно раскладывать на множители. Неразложимые множители и будут простыми элементами. Теперь реализуем эту идею аккуратно. Запустим индукцию по степени 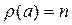элемента “a”. База индукции – неразложимые элементы (независимо от их степени, так что, фактически, имеет место двойная индукция).

Шаг индукции. Пусть 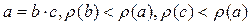, тогда, по предположению индукции сомножители b и c имеют разложение на простые множители, а значит, разложим и исходный элемент “a”.

Самый трудный случай. Пусть 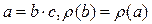, т.е. один из сомножителей не уменьшил свою степень, это допускается определением степени. Тогда применим деление с остатком, «непокорный» элемент “b” поделим на элемент a: .

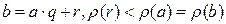Следовательно, 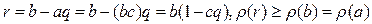. Чтобы не возникло противоречия , остается согласиться, что 1–cq=0, т.е. cq=1. Значит элементы a и b ассоциированы, т.е., “а” – и принадлежит базе индукции.

□

Для кольца с разложением на простые множители есть простой критерий, когда оно является факториальным. Доказательство критерия можно посмотреть, например, в учебнике А.И. Кострикина Введение в алгебру.