ОБЪЕДИНЕНИЕ БАЙЕСОВСКИХ ПРОЦЕДУР С ЛИНГВИСТИЧЕСКИМ ПЕРЕЧИСЛЕНИЕМ
Процедура объединения лингвистического перечисления, обеспечивающего поиск наилучшей пробной грамматики для данной выборки, и статистического подхода к грамматическому выводу базируется на учете вероятности появления предложения. Пусть G – порождающая грамматика, а S(G) – стохастическая грамматика, которая получается из G, если каждой ее продукции 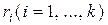 приписать вероятностную меру
приписать вероятностную меру 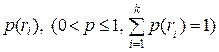 . Этой мерой оценивается вероятность применения к цепочке r продукции
. Этой мерой оценивается вероятность применения к цепочке r продукции 
Сказанное иллюстрируется примером в виде табл. 11 и 12.
Таблица 11
| Продукция | Вероятность применения |
| S1 S ® aA | 2/3 |
| S2 S ® aSB | 1/3 |
| A1 A ® bA | 1/4 |
| A2 A ® b | 3/4 |
| B1 B ® cB | 1/4 |
| B2 B ® c | 3/4 |
Таблица 12
Вывод цепочки 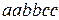
| Цепочка | Продукция | Вероятность |
| S | S2 | 1/3 |
| aSB | B1 | 1/4 |
| aScB | B2 | 3/4 |
| aScc | S1 | 2/3 |
| aaAcc | A1 | 1/4 |
| aabAcc | A2 | 3/4 |
| aabbcc | – | – |
Вероятность 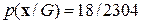 порождения цепочки
порождения цепочки 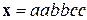 определяется перемножением вероятностей из правого столбца таблицы 12. Незначительность данной величины обусловлена тем, что любое конкретное предложение языка всегда имеет небольшую вероятность.
определяется перемножением вероятностей из правого столбца таблицы 12. Незначительность данной величины обусловлена тем, что любое конкретное предложение языка всегда имеет небольшую вероятность.
Две стохастические грамматики, порождающие один и тот же язык, могут отличаться вероятностями появления отдельных предложений. Рассмотрим пример, в котором экспериментатор выбирает грамматику 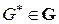 с целью написания предложений выборки, определяющей эту грамматику. Если обозначить p(G) – вероятность выбора любой конкретной грамматики
с целью написания предложений выборки, определяющей эту грамматику. Если обозначить p(G) – вероятность выбора любой конкретной грамматики 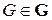 для использования ее в качестве
для использования ее в качестве 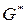 и предположить, что обучающая машина (или машина вывода) может вычислить априорной вероятностью
и предположить, что обучающая машина (или машина вывода) может вычислить априорной вероятностью 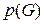 выбора G. Для вывода
выбора G. Для вывода 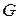 по
по 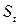 применим байесовскую процедуру и определим апостериорную вероятность
применим байесовскую процедуру и определим апостериорную вероятность
 (68)
(68)
Поскольку выражение (68) содержит суммирование по бесконечному множеству G, вычислить его достаточно сложно даже в тех случаях, когда не все его элементы различны. Эта трудность обходится путем ограничения вычислений множеством G* грамматик, априорные вероятности 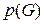 которых превышают некоторое произвольно малое число
которых превышают некоторое произвольно малое число  . Однако если ограничиться лишь каким-то подмножеством G* множества
. Однако если ограничиться лишь каким-то подмножеством G* множества 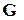 возможных грамматик, то с некоторой произвольно малой вероятностью G* может оказаться вне рассматриваемого множества, т. е. будет принадлежать G – G*.
возможных грамматик, то с некоторой произвольно малой вероятностью G* может оказаться вне рассматриваемого множества, т. е. будет принадлежать G – G*.
Указанная проблема решается минимизацией функции несовместимости
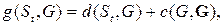 (69)
(69)
где 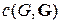 – функция внутренней сложности, равная
– функция внутренней сложности, равная
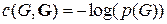 , (70)
, (70)
а 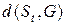 – функция сложности вывода, отражающая вероятность появления выборки
– функция сложности вывода, отражающая вероятность появления выборки 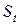 , равная
, равная
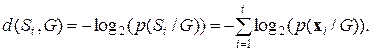 (71)
(71)
Предположим, множество грамматик 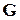 упорядочено по возрастанию априорных вероятностей его грамматик:
упорядочено по возрастанию априорных вероятностей его грамматик: 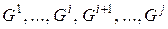 .
.
Байесовское решающее устройство на каждом этапе процесса вывода должно выбирать единственную грамматику так, чтобы величина
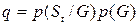 (72)
(72)
была максимальной. Это эквивалентно минимизации функции несовместимости 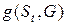 .
.
Отсюда видно, что байесовская процедура перечисления, минимизирующая на каждом шаге процесса перечисления функцию несовместимости, выбирает ту же грамматику. Следовательно, можно построить байесовский алгоритм вывода, который позволяет находить для каждой выборки оптимальную грамматику.
Дата добавления: 2016-01-20; просмотров: 611;
