Статистические ряды распределения
Статистический ряд распределения – это упорядоченное распределение единиц совокупности на группы по определенному варьирующему признаку.
Различают атрибутивные и вариационные ряды распределения.
Атрибутивными называют ряды распределения, построенные по качественным признакам.
Ряд распределения принято оформлять в виде таблиц.
Пример атрибутивного ряда распределения представлен в таблице 3.4.
Таблица 3.4 – Распределение видов юридической помощи, оказанной адвокатами гражданам одного из регионов РФ в 2009г.
| № п/п | Вид юридической помощи, оказанной адвокатами | Число случаев юридической помощи | |
| Всего, тыс. | % к итогу | ||
| Устные советы | 5 109 | 69,43 | |
| Составление документов | 13,47 | ||
| Поручения по ведению уголовных дел | 13,87 | ||
| Поручения по ведению гражданских дел | 3,23 | ||
| Всего | 7 359 | 100,00 |
Представленный ряд показывает, как общее число случаев юридической помощи адвокатов распределялось по видам и формам правовой помощи в 2009 году.
Атрибутивные ряды распределения характеризуют состав совокупности по тем или иным существенным признакам. Взятые за несколько периодов, эти данные позволят исследовать изменение структуры.
Вариационныминазывают ряды распределения, построенные по количественному признаку. Любой вариационный ряд состоит из двух элементов: вариантов и частот.
Вариантамисчитаются отдельные значения признака, которые он принимает в вариационном ряду, т.е. конкретное значение варьирующего признака.
Частоты– это численности отдельных вариантов или каждой группы вариационного ряда, т.е. те или иные варианты в ряду распределения. Сумму всех частот определяет численность всей совокупности, ее объем.
Частоты, выраженные в долях единицы или в %-х к итогу, называются частостями. Сумма частостей равна 1 или 100%.
В зависимости от характера вариации признака различают дискретные и интервальные вариационные ряды.
Дискретный вариационный рядхарактеризует распределение единиц совокупности по дискретному признаку, т.е. величина количественного признака принимает только целые значения.
Пример дискретного вариационного ряда распределения представлен в таблице 3.5.
Таблица 3.5 - Распределение семей по числу занимаемых комнат в отдельных квартирах в 2009г. в РФ
| № п/п | Группы семей, проживающих в квартирах с числом комнат | Число семей | |
| Всего, тыс. ед. | В % к итогу | ||
| 16,3 | |||
| 49,7 | |||
| 30,7 | |||
| 4 и более | 3,3 | ||
| Всего | |||
| варианты | частоты | частости |
Построение интервальных вариационных рядов целесообразно, прежде всего, при непрерывной вариации признака (в случае непрерывной вариации величина признака у единиц совокупности может принимать в определенных пределах любые значения), а также, если дискретная вариация проявляется в широких пределах, т.е. число вариантов дискретного признака достаточно велико.
Удобнее всего ряды распределения анализировать при помощи их графического изображения, позволяющего также судить о форме распределения. Наглядное представление о характере изменения частот вариационного ряда дают полигон и гистограмма.
Полигониспользуется при изображении дискретных вариационных рядов. Для его построения по оси абсцисс в одинаковом масштабе откладываются ранжированные значения варьирующего признака, а по оси ординат – частоты или частности. Полученные на пересечении точки соединяются прямыми линиями, т.е. получается ломаная линия, называемая полигоном частот.
Гистограммаприменяется для изображения интервального ряда. На оси абсцисс откладывают интервалы ряда, высота которых равна частотам, отложенным на оси ординат. Над осью абсцисс строятся прямоугольники, площадь которых соответствует величинам произведений интервалов на их частоты.
По данным таблицы 3.6 построим полигон распределения рабочих по тарифному разряду.
Таблица 3.6 - Распределение рабочих по тарифному разряду
| Тарифный разряд | Численность рабочих, чел. |
| Всего |
На рисунке 3.1 изображен полигон, построенный по данным таблицы 3.6.
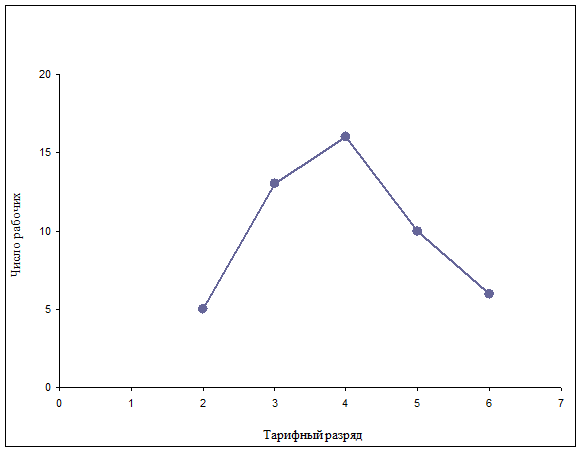
Рисунок 3.1 – Полигон распределения 50 рабочих по тарифному разряду
Пример построения гистограммы по данным таблицы 3.7 показан на рисунке 3.2.
Таблица 3.7 – Распределение заводов по стоимости основных фондов
| Стоимость основных фондов, млн. руб. | Число заводов, ед. |
| 5-7 | |
| 7-9 | |
| 9-11 | |
| 11-13 | |
| 13-15 | |
| Всего |
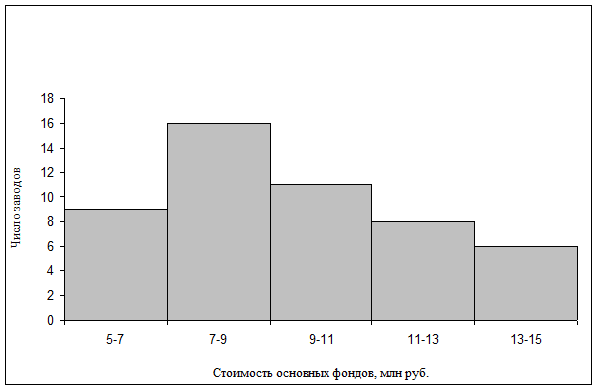
Рисунок 3.2 – Гистограмма распределения 50 заводов по стоимости основных фондов
Одним из важнейших требований, предъявляемых к статистическим рядам распределения, являетсяобеспечение сравнимости их во времени и пространстве.
Вариационные ряды с равными интервалами обеспечивают это условие. В рядах с неравными интервалами для обеспечения необходимой сравнимости исчисляют плотность распределения, т.е. определяют, сколько единиц в каждой группе приходится на единицу величины интервала. Например, распределение магазинов по размеру товарооборота, представленное в таблице 3.8.
Таблица 3.8 - Распределение магазинов по размеру товарооборота
| Группы магазинов по размеру товарооборота, тыс. руб. | Число магазинов | Величина интервала, тыс. руб. | Плотность распределения, ед. (гр.2/гр.3) |
| До 50 | 0,5 | ||
| 50 - 120 | 0,64 | ||
| 120 - 250 | 0,5 | ||
| Продолжение табл. 3.8 | |||
| 250 - 450 | 0,4 | ||
| 450 - 980 | 0,04 | ||
| Итого |
При построении графика распределения вариационного ряда с неравными интервалами высоту прямоугольников определяют пропорционально показателям плотности распределения значений изучаемого признака в соответствующих интервалах.
Дата добавления: 2016-01-20; просмотров: 2432;
