Система сходящихся сил в пространстве.

Системой сходящихся сил называют такую систему сил, линии действия которых пересекаются в одной точке - центре пучка. Пусть задана произвольная система сходящихся сил 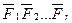приложенных к твердому телу. Перенесем эти силы как скользящие векторы в точку пересечения линий их действия. Затем, пользуясь аксиомой о параллелограмме сил, найдем равнодействующую этих сил. Равнодействующая такой системы может быть определена графически и аналитически. Для аналитического определения равнодействующей силы следует выбрать систему прямоугольных осей координат и воспользоваться теоремой из геометрии о том, что проекция замыкающей любого многоугольника на какую-либо ось равна алгебраиче­ской сумме проекций составляющих его сторон на ту же ось. Проецируя векторы векторного равенства на прямоугольные оси координат, согласно теореме о проекции замыкающей получим:

, , .

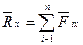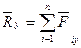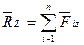По проекциям определяем модуль = действующей силы и косинусы углов ее с осями координат по формулам :

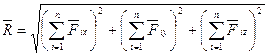
и cos(Rx^x)=Rx / R,

cos (Ry^y)=Ry / R,

cos (Rz^z)=Rz/R.

Таким образом, система n сходящихся сил эквива­лентна одной силе 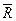, которая и является равнодействующей этой системы сил.

Процесс последовательного применения правила параллелограмма приводит к построению многоугольника из заданных сил.

В силовом многоугольнике конец одной из сил служит началом другой. Равнодействующая сила 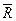в сило­вом многоугольнике соединяет начало первой силы с концом последней, т. е. изображается замыкающей силового многоугольника.