Приведение пространственной системы сил к вектору и к главному моменту.

Приведение пространственной системы сил к главному вектору и к главному моменту. Пусть на абсолютно твердое тело действует произвольная простран­ственная система сил 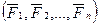, тогда справедлива теорема.

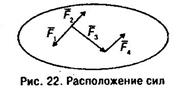
Эта система сил может быть заменена одной силой 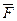и парой сил, момент которой 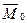. Причем сила 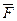, называемая главным вектором пространственной системы сил, определяется формулой: 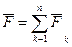(1) и приложена в выбранном центре О. А момент 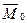, называемый главным моментом пространственной системы сил, определяется формулой 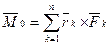(2) , т. е. равен геометрической сумме моментов всех сил системы относительно выбранного центра приведения.

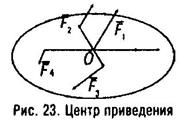
Доказательство этого утверждения основывается на лемме о параллельном пе­реносе сил. В соответствии с ней все силы исходной системы перенесем параллельно себе в выбранную точку приведения О, при этом получим систему исходящих сил. Как из­вестно, такая система может быть заменена равнодействующей 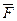, приложенной в точке О и определя­емой формулой (1). В соответствии с леммой, для того чтобы состояние тела не изменилось при вы­полненном переносе сил, необходимо к телу приложить n пар сил, моменты которых относительно центра О определялись соотношениями: 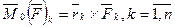(3).По теореме о сложении пар сил эта система пар сил может быть заменена одной парой, момент которой равен геометрической сумме моментов указанных пар сил и определялся формулой (2). Главный момент М_о этой результирующей пары обычно изображают при­ложенным в центре О, хотя он является свободным вектором и может переноситься параллельно себе в пространстве.