Существуют два типа sci-файлов: файл-сценарий и файл-функция.

Файл-сценарий (Script-файл) представляет собой последовательность команд без входных и выходных параметров. Он имеет следующую структуру:

// Kомментарий

Тело файла с любыми выражениями

Пример:

//Plot with color red

// Строит график синусоиды линией красного цвета

// в интервале [0, pi]

x=0: .1: %pi; plot(x, sin(x), 'r')

Файл-функция имеет следующую структуру:

function[y1,...,yn]=fun(x1,...,xm)

Тело функции

Endfunction

Здесь

fun - имя функции,

xi - входные аргументы функции (их m штук),

yi - выходные аргументы функции (их n штук).

Пример.

Вычисление факториала.

function [x]=fact(k)

k=int(k)

if k<1 then k=1, end

x=1;

for j=1:k,x=x*j;end

endfunction

Наберем этот текст в любом текстовом редакторе и сохраним его в файле с именем fact.sci. Расширение *.sci является для Sclab "родным", но не обязательным. Затем следует вызвать эти файлы из Scilab c помощью команд getf(filename) или exec(filename,-1); Те же операции можно произвести с помощью команд меню File-getf или File-exec.

До вызова функции желательно проверить, не была ли уже загружена такая функция ранее. Для этого:

exists('fact')

Результат:

ans =

0.

После загрузки файла

-->exec('C:\fact');

набираем

-->x=fact(5)

x =

120

Пример:

function z=fun(x, y)

// Определение функции

z=x.^2 + y.^2;

endfunction

Сохраним эту функцию под именем fun.sci. После загрузки функции в Scilab мы можем обратиться к ней:

-->fun(1,2)

ans =

5.

Пример. Даны два массива X и Y. Вывести в командное окно имя массива, содержащего наибольшее число элементов, кратных числу три.

Решение. Составим программу и сохраним ее под именем t.sci в каталоге C:\DOCUME~1\user\.

function g=t(v)

s=0; n=length(v);

for i=1:n

if modulo(v(i), 3)==0 then

s=s+1;

end

end

g=s;

endfunction

Далее сохраним в корневом каталоге C:\ под именем tot, а затем выполним программу

x=[1 2 3 5 7 6 12]; y=[5 7 24 15]; d1=t(x), d2=t(y)

if d1>d2 then

disp('x')

elseif d1==d2 then

disp('в обоих массивах это число одинаково')

else

disp('y')

end

Получим ответ:

d1 =

3.

d2 =

2.

x

Запуск файла на выполнение осуществляется так:

-->scipad('C:\DOCUME~1\user\t.sci');

-->scipad('C:\tot');

-->exec('C:\tot');

Файл-функция был сохранен в 'C:\DOCUME~1\user\t.sci', файл-сценарий – в 'C:\tot'

Это эквивалентно выполнению следующих операций: запускаем Scilab.

Далее: открываем файл-функцию File/Open… Далее Execute/Load into Scilab; Открываем файл-сценарий (выполняемый файл) File/Open…Далее File/Exec …

Открываются файлы в окне Scilab.

Если выходных параметров несколько, то их надо указать в квадратных скобках после слова function.

function [var1, var2, …] = fname(список_параметров)

// Основной комментарий

// Дополнительный комментарий

Тело файла с любыми выражениями

var1=выражение

var2=выражение

…

endfunction

Пример. Задан вектор 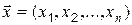. Вычислить 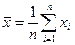и

.

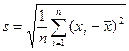Решение. Набираем и сохраняем в редакторе под именем statv.sci файл

function[mean, stdev] = statv(x)

n=length(x);

mean=sum(x)/n;

stdev=sqrt(sum((x-mean).^2)/n);

endfunction

Далее в командном окне набираем

--> v=[1, 2, 3, 4, 5];

--> [a, m]=statv(v)

В строках вывода получаем:

m =

1.4142136

a =

3.

-->

Краткий комментарий к программе.

Во второй строке файла statv.sci вычисляется количество элементов в массиве x; sum(x) – суммируются все элементы массива x; mean – вычисляется 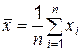; stdev – вычисляется 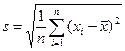. В итоге получаем среднее значение , .

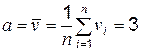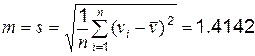Для создания временной задержки выполнения программы служит команда xpause, которая приостанавливает текущий процесс на число микросекунд, указанных в скобках

· хpause(microsecs)

Пример:

xbasc();

xset("color",12);

xstring(1,1,"Blue");

xpause(5.e6); // временная задержка на 5 секунд

xbasc();

xset("color",5);

xstring(0,1,"Red");

В результате мы видим в графическом окне вначале надпись "Blue", а затем она исчезает и мы видим сдвинутую по горизонтали надпись "Red".

Некоторые полезные функции Scilab для вычисления целой части числа:

int(1.9999)=1=int(1.1) int(-1.9999)=-1 int(-0.00001)=0

floor(1.5)=1=floor(1.9)=floor(1.1) floor(-1.1)=-2=floor(-1.8)

ceil(1.1)=ceil(1.9)=2 ceil(-1.9)=-1=ceil(-1.2)

fix(-1.2)=-1=fix(-1.7) fix(1.7)=1=fix(1.2)