Исходные данные для факторного анализа
| Показатели | Условные обозначения | Базисные значения (0) | Фактические значения (1) | Изменение | |
| Абсолютное (+,- ) | Относительное (%) | ||||
| Объем товарной продукции, тыс. руб. | ТП | +480 | 116,40 | ||
| Количество работников, чел | Ч | +5 | 125,00 | ||
| Выработка на одного работающего, тыс. руб. | СВ | -10 | 93,15 |
Анализ влияния на объем товарной продукции количества работников и их выработки проведем описанным выше способом на основе данных табл.2. Зависимость объема товарной продукции от данных факторов можно описать с помощью мультипликативной модели:
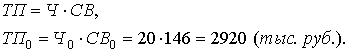
Тогда влияние изменения величины количества работников на обобщающий показатель можно рассчитать по формуле:
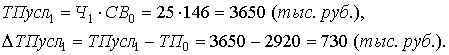
Далее определим влияние изменения выработки работников на обобщающий показатель
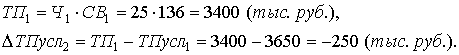
Таким образом, на изменение объема товарной продукции положительное влияние оказало изменение на 5 человек численности работников, что вызвало увеличение объема продукции на 730 тыс. руб. и отрицательное влияние оказало снижение выработки на 10 тыс. руб., что вызвало снижение объема на 250 тыс. руб. Суммарное влияние двух факторов привело к увеличению объема продукции на 480 тыс. руб.
Преимущества данного способа: универсальность применения, простота расчетов.
Недостаток метода состоит в том, что, в зависимости от выбранного порядка замены факторов, результаты факторного разложения имеют разные значения. Это связано с тем, что в результате применения этого метода образуется некий неразложимый остаток, который прибавляется к величине влияния последнего фактора. На практике точностью оценки факторов пренебрегают, выдвигая на первый план относительную значимость влияния того или иного фактора. Однако существуют определенные правила, определяющие последовательность подстановки:
− при наличии в факторной модели количественных и качественных показателей в первую очередь рассматривается изменение количественных факторов;
− если модель представлена несколькими количественными и качественными показателями, последовательность подстановки определяется путем логического анализа.
Под количественным факторами при анализе понимают те, которые выражают количественную определенность явлений и могут быть получены путем непосредственного учета (количество рабочих, станков, сырья и т.д.).
Качественные факторы определяют внутренние качества, признаки и особенности изучаемых явлений (производительность труда, качество продукции, средняя продолжительность рабочего дня и т.д.).
Способ абсолютных разниц является модификацией способа цепной подстановки. Изменение результативного показателя за счет каждого фактора способом разниц определяется как произведение отклонения изучаемого фактора на базисное или отчетное значение другого фактора в зависимости от выбранной последовательности подстановки:
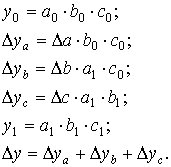
Способ относительных разниц применяется для измерения влияния факторов на прирост результативного показателя в мультипликативных и смешанных моделях вида у = (а – в) . с. Он используется в случаях, когда исходные данные содержат определенные ранее относительные отклонения факторных показателей в процентах.
Для мультипликативных моделей типа у =а. в. с методика анализа следующая:
· находят относительное отклонение каждого факторного показателя:
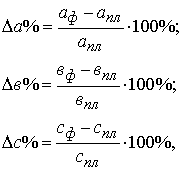
· определяют отклонение результативного показателя у за счет каждого фактора
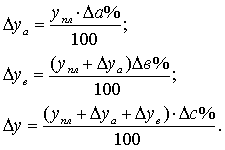
Пример. Воспользовавшись данными табл. 2, проведем анализ способом относительных разниц. Относительные отклонения рассматриваемых факторов составят:
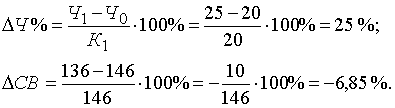
Рассчитаем влияние на объем товарной продукции каждого фактора:
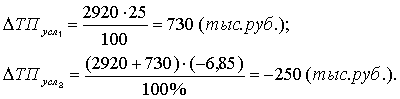
Результаты расчетов те же , что и при использовании предыдущего способа.
Интегральный метод позволяет избежать недостатков, присущих методу цепной подстановки, и не требует применения приемов по распределению неразложимого остатка по факторам, т.к. в нем действует логарифмический закон перераспределения факторных нагрузок. Интегральный метод позволяет достигнуть полного разложения результативного показателя по факторам и носит универсальный характер, т.е. применим к мультипликативным, кратным и смешанным моделям. Операция вычисления определенного интеграла решается с помощью ПЭВМ и сводится к построению подынтегральных выражений, которые зависят от вида функции или модели факторной системы.
Можно использовать также уже сформированные рабочие формулы, приводимые в специальной литературе [4]:
1. Модель вида 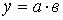 :
:
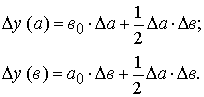
2. Модель вида 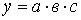 :
:
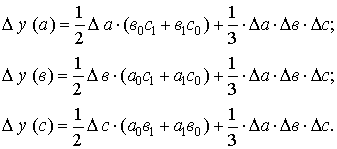
3. Модель вида 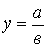 :
:
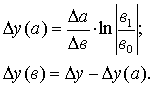
4. Модель вида 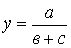 :
:
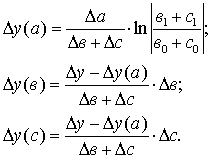
Рассмотрим возможность использования основных методов детерминированного анализа, обобщив вышеизложенное в виде матрицы (табл.3).
Таблица 3
Дата добавления: 2016-01-20; просмотров: 1351;
