Внезапное 3-х фазное КЗ в простейшей электрической цепи

Рассмотрим электрическую цепь (Рис.31), в которой имеется источник неограниченной мощности (т.е. подведенное к цепи синусоидальное напряжение остается неизменным по амплитуде), кабельная (воздушная) линия и точка КЗ.

Рис. 31

Напряжение источника изменяется по синусоидальному закону

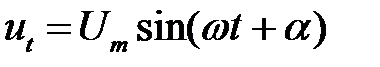
Ток режима, предшествующего короткому замыканию, может быть определен так:

,

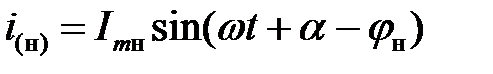где I_mн=U_m/Z_н– амплитуда тока предшествующего режима,

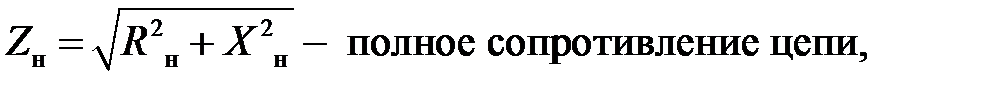
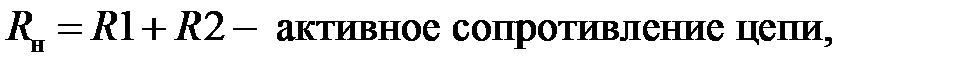
α– фаза напряжения(включения),

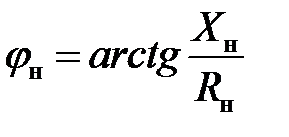- угол сдвига между напряжением и током.

При внезапном КЗ происходит внезапное изменение сопротивления цепи. Поскольку цепь содержит индуктивное сопротивление, то ток не может мгновенно достигнуть максимума, а происходит постепенное изменение тока, что объясняется инерцией магнитного потока. После возникновения 3-х фазного КЗ схема распадается на две независимые цепи, одна из которых остается присоединенной к источнику, а вторая превращается в короткозамкнутый контур, ток в котором будет поддерживаться до тех пор, пока запасенная в нем энергия магнитного потока не перейдет в тепло, поглощаемое активным сопротивлением этого контура. Для этой части схемы уравнение баланса напряжений в каждой фазе имеет вид:

.

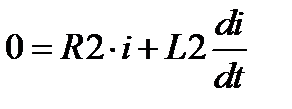Его решение общеизвестно

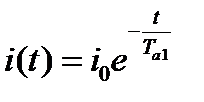, где

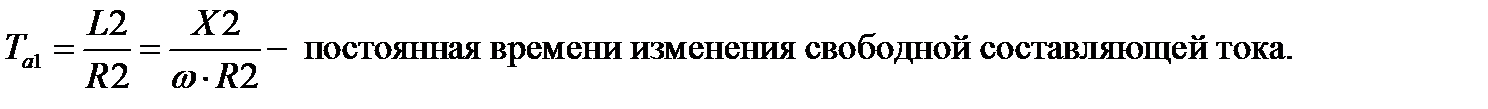
Т.е. ток в этой части схемы будет затухать по экспоненте (Рис.32) с одной и той же постоянной времени Т_а1. Кроме этого, следует отметить, что: 1) начальные значения токов в каждой из фаз в общем случае различны за счет фазового сдвига и определяются проекциями на линию времени tсоответствующих вращающихся векторов; 2) начальные значения тока ни в одной из фаз не могут превышать амплитуду тока предшествующего режима.

Рис. 32

Рассмотрим протекание переходного процесса на участке цепи слева от точки КЗ, получающем питание от источника бесконечной мощности. Мгновенные значения тока и приложенного напряжения для фазы А связаны между собой дифференциальным уравнением:

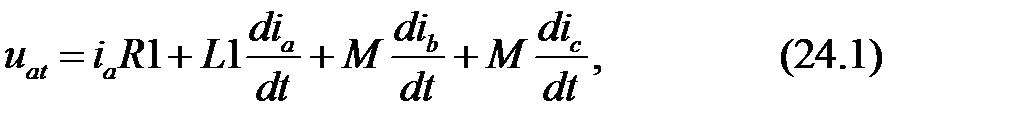
Имея ввиду, что

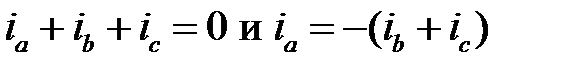
уравнение (24.1) можно представить как

или

где

Общее решение уравнения (24.3) имеет вид:

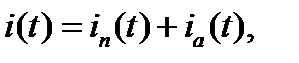
где i_n(t) – вынужденная (периодическая) составляющая тока КЗ;

i_a(t) – апериодическая (свободная) составляющая тока КЗ.

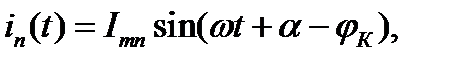
здесь

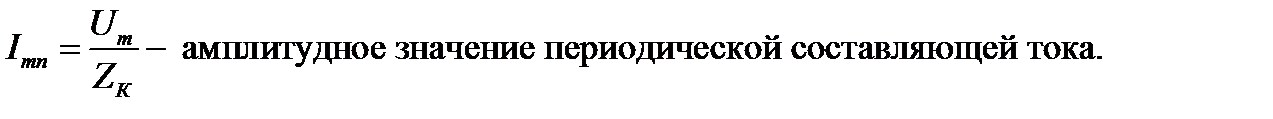
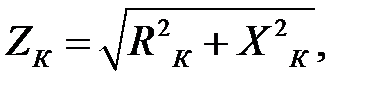
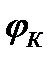- угол сдвига между током и напряжением фазы при КЗ.

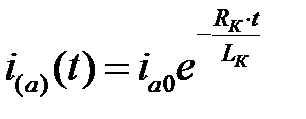
тогда

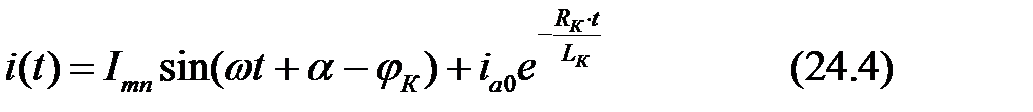
Первый член этого выражения представляет собой периодическую слагающую тока КЗ, которая при рассматриваемых условиях (U_m=const) по амплитуде остается неизменной и является вынужденным током нового режима.

Обозначив T_a=L_k/R_k– постоянная времени изменения свободной составляющей тока КЗ, тогда получим

Начальное значение апериодической составляющей iaoопределяется из закона инерции магнитного потока. В начальный момент КЗ сумма вынужденного и свободного токов равна току, который был в фазе в момент возникновения КЗ приt=0, т.е

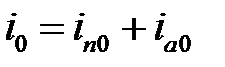
Отсюда имеем:

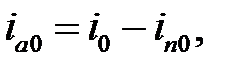
где io– ток нарушения режима при (t=-0), а ino– ток в момент нарушения режима при (t=+0)

или

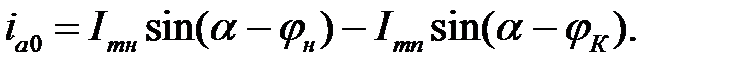
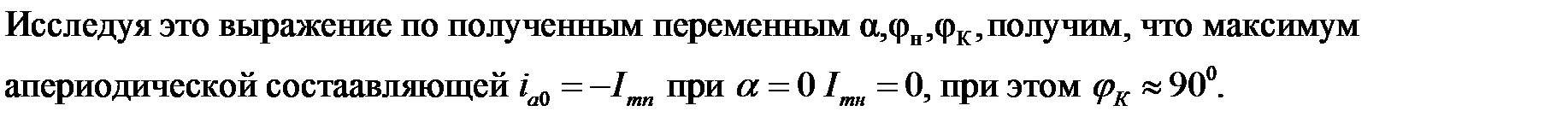
Максимальное начальное значение апериодической составляющей тока КЗ называется сверхпереходным током и обозначается I"_m, т. е. I"_m=I_mп

Тогда полный ток КЗ при отсутствии предшествующего тока (I_mн=0) будет

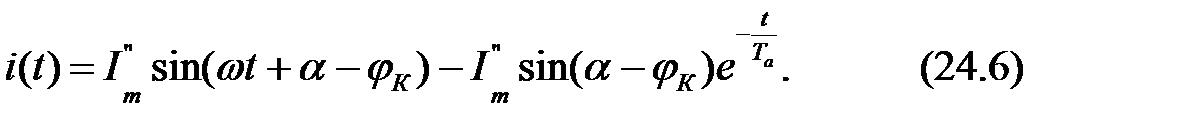
Изменение во времени полного тока КЗ и его составляющих показано на Рис.33.

Рис.33

Наибольшего значения полный ток КЗ достигает при наибольших значениях его составляющих.

Полный ток КЗ несимметричен относительно оси времени. Наличие апериодической составляющей тока искажает форму полного тока КЗ и делает ее несимметричной относительно оси времени.

Максимальное мгновенное значение полного тока КЗ (пик тока) называется ударным током КЗ (iу). Он наступает приблизительно через полпериода, что при частоте 50 Гц составляет 0,01с с момента КЗ. В соответствии с общим выражением (24.6) для ударного тока КЗ имеем:

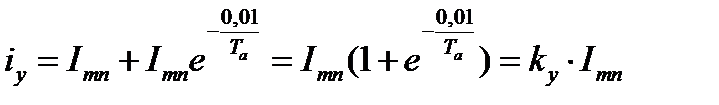
где

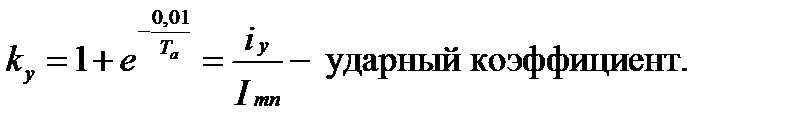
Ударный коэффициент kу показывает превышение величины ударного тока над амплитудой периодической составляющей .

Поскольку Т_а может изменятся от Т_а=0 (L_k=0) до Т_а=∞ (R_k=0), то величина ударного коэффициента находится в пределах 1≤kу≤ 2

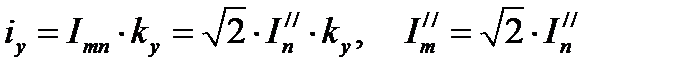
где 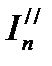– действующее значение периодической составляющей сверхпереходного тока КЗ.