ЭЛЕКТРОМАГНИТНЫЕ ПЕРЕХОДНЫЕ ПРОЦЕССЫ

В ПРОСТЕЙШИХ 3-ФАЗНЫХ ЦЕПЯХ

Простейшей называют симметричную 3-фазную цепь с сосредоточенными параметрами при отсутствии в ней трансформатора. Питание осуществляется от источника бесконечной мощности, который характеризуется тем, что его собственное сопротивление равно нулю, а напряжение, изменяясь с постоянной частотой, имеет неизменную амплитуду.

К задачам такого рода относятся исследования переходных процессов в элементах системы электроснабжения, имеющих большую электрическую удаленность от источников энергии. При этом мощность источников на два и более порядков превосходит мощность потребителей системы электроснабжения.

Целью таких задач является выработка инженерной методики количественной и качественной оценки параметров режима, определение экстремальных значений параметров аварийных переходных режимов.

Переходные процессы в неразветвленных цепях

Анализ переходных процессов в 3-фазных неразветвленных цепях можно выполнить с использованием обобщенной электрической схемы (рис. 2.1)

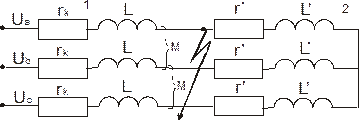
Рис. 2.1. Простейшая 3-фазная электрическая цепь

Фазные напряжения для данной схемы можно определить:

u_B = U_m sin (wt+a-120 ⁰),

u_C = U_m sin (wt+a-240 ⁰),

где U_m - амплитуда напряжений;

a - фаза включения;

t - время.

В точке К в момент времени t = 0 возникает 3-фазное металлическое замыкание (замыкание между фазами через пренебрежимо малое переходное сопротивление).

После возникновения короткого замыкания схема распадается на две независимые части, причем во второй части цепи отсутствуют источники. Следовательно, в этой части будут иметь место только процессы рассеяния запасов энергии.

,

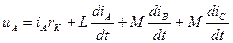где М – коэффициент взаимной индукции.

,

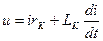где r_K – активное сопротивление в цепи короткого замыкания;

L_K – результирующая индуктивность фазы, L_K = L - M.

,

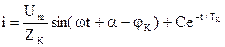где Z_{K –} модуль полного сопротивления цепи короткого замыкания;

j_К – угол фазы сдвига тока в цепи короткого замыкания;

a – угол, определяющий U_A при t = 0 (фаза включения);

С – постоянная, определяемая из начальных условий;

Т_К – постоянная времени цепи короткого замыкания,

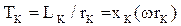,T_K = L / r = x _K / (ω r_K),

x_K – индуктивное сопротивление в цепи короткого замыкания.

Первое слагаемое правой части уравнения (2.4) – принужденный ток нового режима, постоянный по амплитуде:

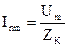Вторая составляющая тока КЗ – апериодическая. Она затухает по экспоненциальному закону с постоянной времени Т_К.

Начальное значение апериодической составляющей тока короткого замыкания найдем из условия неизменности тока в первый момент короткого замыкания (t = 0) .

,

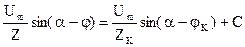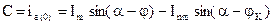где I_m, j - амплитуда и фаза тока в режиме, предшествующем короткому замыканию.

i = i_n + i_a = I_nmsin(ωt + α – φ_к) + [I_msin(α – φ) – I_m sin(α – φ_к)]e^—t/Tк ,

где i_n - мгновенное значение периодической составляющей т.КЗ

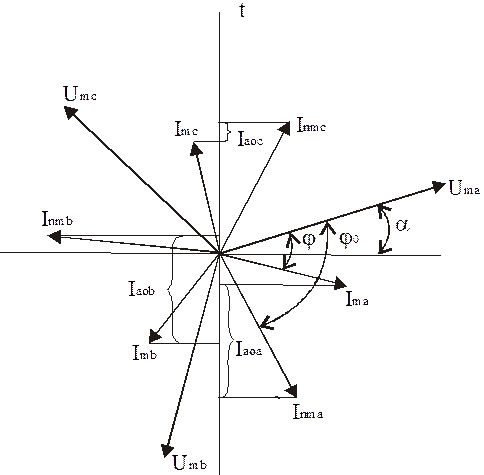
Рис. 2.2. Векторная диаграмма для начального момента трехфазного короткого замыкания.

Начальное значение апериодической составляющей на основании (2.8) определяется графически как разность проекций на ось времени периодических составляющих доаварийного и аварийного тока (I_m и I_mn на рис. 2.2). Для каждой из фаз оно имеет свою величину в зависимости от пространственного положения этих векторов в момент аварии.

Апериодическая составляющая тока короткого замыкания является как бы криволинейной осью, на которую наложена его периодическая составляющая. Обычно апериодическая составляющая затухает за 0,1-0,3 до пренебрежимо малой величины.

Постоянная затухания периодической составляющей Т_а - это время, в течение которого ток снижается до 0,368 своего первоначального значения.

Рис. 2.3. Изменение полного тока и его составляющих в разных фазах

при внезапном трехфазном коротком замыкании