Напряженное состояние при растяжении (сжатии)

В начале курса при первом знакомстве с понятием «напряжение» было подчеркнуто, что нельзя говорить о напряжении в данной точке тела, не указывая положения площадки, на ко­торой оно возникает. Действительно, через точку можно прове­сти бесчисленное множество различно ориентированных пло­щадок, и, конечно, в общем случае нет никаких оснований предполагать, что возникающие на них напряжения одинаковы.

Совокупность нормальных и касательных напряжений, воз­никающих на всем бесчисленном множестве площадок, ко­торые можно провести через данную точку, характеризует на­пряженное состояние в этой точке.

Исследовать напряженное состояние в данной точке — это значит получить зависимости, позволяющие определить напря­жения, возникающие в любой проведенной через нее площадке. Для решения этой задачи надо знать напряжения по любым трем взаимно перпендикулярным площадкам, проведенным че­рез исследуемую точку (доказательства этого положения не приводим). Эти площадки и возникающие на них напряжения (они, повторяем, должны быть известны) называют исходными.

При исследовании напряженного состояния в различных точках прямого бруса в любом случае его нагружения ис­ходными являются напряжения, возникающие на площадках, соответствующих поперечному и двум продольным сечениям, проходящим через рассматриваемую точку. При растяжении (сжатии) прямого бруса в поперечных сечениях возникают только нормальные напряжения, определяемые по формуле:

σ_z=N/A (2.5.1)

Индекс z показывает, что это напряжение возникает на пло­щадке, нормаль к которой параллельна оси z . В продольных сечениях нет ни нормальных, ни касательных напряжений.

Отсутствие нормальных напряжений в продольных сечениях является следствием того, что при растяжении (сжатии) нет взаимного надавливания волокон бруса. В отсутствии касательных напряжений легко убедиться, рассекая брус продольной плоскостью и рассматри­вая условие равновесия одной из его отсеченных частей,

Для исследования напряженного состояния мысленно выре­жем вокруг произвольной точки бруса бесконечно малый па­раллелепипед (рис. 2.5.3, а). В дальнейшем такие элементарные параллелепипеды будем называть элементами или частицами.

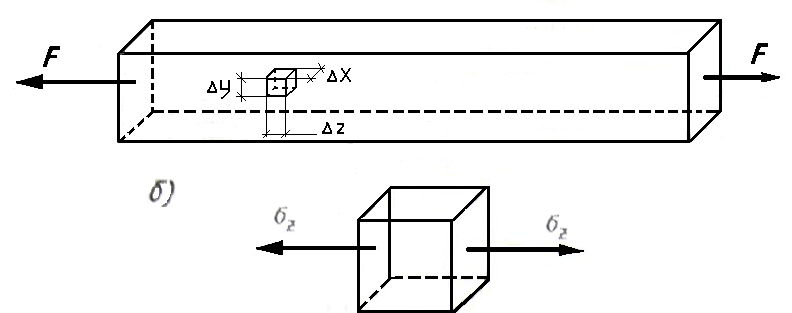
Рисунок 2.5.3

В рассматриваемом случае совершенно безразлично, где имен­но вырезать эту частицу, так как напряженное состояние всех точек бруса одинаково - однородное напряженное состояние.

Для того чтобы выделенный элемент находился в равнове­сии, следует приложить к его граням внутренние силы, заме­няющие действие отброшенных частей тела (бруса) на оста­вленную. Обращаем внимание, что здесь мы поступаем в полном соответствии с требованиями метода сечений, но ес­ли ранее при определении продольных сил было достаточно рассечь брус плоскостью, совпадающей с интересующим нас поперечным сечением, то новая задача — исследование напря­женного состояния — потребовала иного применения этого ме­тода: элемент вырезан шестью сечениями.

Выделенный элемент (модель напряженной точки) изобра­жен отдельно на рис. 2.5.3,6. На его гранях, совпадающих с плоскостями поперечного сечения бруса, возникают нор­мальные напряжения, остальные четыре грани от напряжений свободны.