Силы в поперечных сечениях бруса

При растяжении (сжатии) прямого бруса в его поперечных се­чениях возникает только один внутренний силовой фактор — про­дольная сила, обозначаемая N₂ или N.

Прямые брусья, работающие на растяжение или сжатие, часто называют стержнями.

Простейшие случаи растяжения и сжатия представлены на рис. 2.5.1,a и 2.5.2,а: в центрах тяжести торцовых поперечных се­чений бруса приложены две равные и противоположно напра­вленные силы, линии действия которых совпадают с осью бруса.

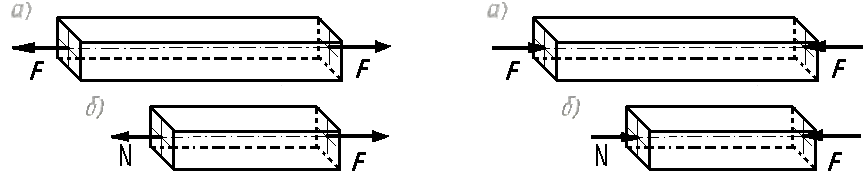
Рисунок 2.5.1 Рисунок 2.5.2

Продольные силы, соответствующие деформации растяже­ния, условимся считать положительными, а сжатия — отрица­тельными. При растяжении продольная сила направлена от се­чения (рис. 2.5.1,6), а при сжатии — к сечению (рис. 2.5.2, б).

При сжатии сравнительно длинного и тонкого бруса прямолиней­ная форма его равновесия может оказаться неустойчивой. В этой лекции будем во всех случаях полагать, что опасность потери устойчивости исключена. Расчеты на устойчивость рассмотрены в лекции 2.9.

Из рассмотренных примеров следует, что, для того чтобы брус работал на растяжение (сжатие), равнодействующая внеш­них сил, приложенных по одну сторону от любого поперечного сечения бруса, должна быть направлена вдоль его оси. Только при этом условии все внутренние силовые факторы, кроме про­дольной силы, будут равны нулю.

Модуль и направление (знак) продольной силы определяют­ся из уравнения равновесия, составленного для отсеченной (оставленной после проведения сечения) части бруса: т. е. продольная сила в произвольном поперечном сечении бруса численно равна алгебраической сумме проекций на его продоль­ную ось всех внешних сил, приложенных к оставленной части.

Направление N противоположно направлению проекции равнодействующей внешних сил, приложенных к оста­вленной части.

Приведенная формулировка не может рассматриваться как определение понятия «продольная сила», она указывает лишь метод для нахождения ее значения и направления.

Продольной силой в поперечном сечении бруса называется равнодействующая внутренних нормальных сил, возникающих в этом сечении.

Допустимо и такое определение: продольной силой в поперечном сечении бруса называется направленная вдоль его оси составляющая главного вектора внутренних сил, возникающих в этом сечении.

Элементарная нормальная сила, возникающая на бесконеч­но малой площадке поперечного сечения, равна произведению нормального напряжения σ_z на площадь dА указанной пло­щадки, т. е. dN=σ_zdA Сумма (равнодействующая) этих эле­ментарных сил представляет собой определенный интеграл: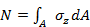

Это математическое выражение эквивалентно приведенному словесному определению понятия «продольная сила».

В тех случаях, когда продольные силы в различных попе­речных сечениях бруса неодинаковы, закон их изменения по длине бруса удобно представить в виде графика, называемого эпюрой продольных сил. Аргументом при построении этого гра­фика является координата поперечного сечения бруса (z), а функцией — продольная сила (N),

Таким образом, эпюра продольных сил это график функ­ции N = f(z). Далеко не всегда можно составить выражение указанной функции, справедливое при всех значениях коор­динаты z (для всего бруса). Приходится разбивать брус на участки, для каждого из которых будет свое выражение функ­ции N = f(z)

Эпюру продольных сил строят в первую очередь для того чтобы использовать ее при расчете бруса на прочность; она дает возможность найти наибольшие значения продольных сил и положение сечений в которых они возникают.