Расчет многоэтажных зданий

Современные многоэтажные здания представляют собой сложные пространственные системы, состоящие из различных элементов и соединений, параметры (жесткость и т.п.) которых изменяются в процессе нагружения. Расчет таких зданий с учетом всех их конструктивных особенностей, характера нагрузок и воздействий является очень трудной задачей. Поэтому реальное сооружение в расчетах заменяется некоторыми идеализированными схемами, с той или иной полнотой отражающими действительную работу сооружения. Степень идеализации зависит от целей расчета, полноты и достоверности исходных данных и т. п.

При проектировании даже при учете только основных особенностей деформирования многоэтажных зданий их расчет производят с помощью ЭВМ. Для целого ряда конкретных сооружений и видов воздействий оказывается возможным использовать еще более упрощенные схемы, например, пространственную систему здания расчленять на части, каждая из которых рассчитывается независимо на приложенные к ней нагрузки как плоская система. В этих случаях для расчета могут использоваться хорошо известные проектировщикам инженерные методы расчета и вспомогательные таблицы. Такой подход оказывается необходимым для предварительной приближенной оценки усилий, возникающих в элементах здания, а во многих случаях он обеспечивает достаточную точность.

Расчет многоэтажных зданий производят на основные и особые сочетания нагрузок (см. гл. 2). При этом необходимо иметь в виду, что при высоте зданий более 40 м учитывают помимо статической ветровой нагрузки динамическую составляющую этой нагрузки. При расчете вертикальных несущих элементов (колонн, стен) суммарные кратковременные нагрузки допускается снижать умножением на коэффициент ψ_n, учитывающий пониженную вероятность одновременного загружения вышерасположенных этажей полной нагрузкой [2].

■ Расчет рамных систем. Расчет начинают с установления погонных жесткостей ригелей и стоек. С этой це­лью предварительно назначают сечения элементов, пользуясь примерами ранее запроектированных аналогичных конструкций или путем приближенного расчета. В последнем случае сечение ригеля определяют по опорному моменту

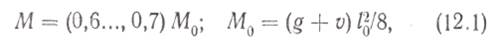
где g и v — постоянная и временная расчетные нагрузки на 1 м ригеля; l₀ — расчетный пролет ригеля.

Тогда

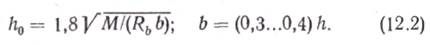
Сечение колонн

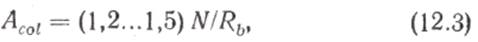
где 1,2...1,5 — коэффициент, учитывающий влияние изгибающего момента в колонне; N — продольная сила, под­считанная в соответствии с грузовой площадью.

По результатам предварительного подбора сечений производят увязку сечений ригелей и колонн между собой и унификацию их размеров. В соответствии с принятыми размерами подсчитывают погонные жесткости ригелей и рам как для бетонных сечений.

Как уже указывалось, для расчета многоэтажных рам составлены программы для ЭВМ. При этом может быть учтена податливость узлов и другие факторы. Наряду с этим не утрачивают своего значения инженерные методы, применяемые при вариантном проектировании, при анализе решений, получаемых с помощью ЭВМ, и т. п. При приближенном расчете инженерным методом пространственный рамный каркас расчленяют на отдельные плоские рамы. Поскольку перемещения каркаса зданий обычно малы, используют принцип независимости действия сил и рассчитывают каждую раму отдельно на приходящиеся на нее вертикальные и горизонтальные нагрузки.

■ Расчет рам на вертикальные нагрузки. Если многоэтажные многопролетные рамы каркасных зданий имеют равные пролеты (или отличающиеся до 20 %), одинаковую высоту этажей, а также одинаковую нагрузку по ярусам, то все узлы стоек таких рам, расположенных на одной вертикали, получают примерно равные углы поворота, в результате возникают равные узловые моменты с нулевыми точками эпюры моментов в середине высоты этажа (рис. 12.6, а). В этом случае многоэтажная рама может быть расчленена на ряд одноэтажных рам трех типов (рис. 12.6. б); верхнего, средних и нижнего этажей. Расчет каждой из этих рам производится по таблицам [24] при наиболее невыгодных сочетаниях постоянных и временных нагрузок. При этом опорные изгибающие моменты в ригелях рамы

где α и β — табличные коэффициенты, зависящие от числа пролетов (два или три), схемы загружения и соотношения жесткостей ригеля и стойки; g и v — постоянная и временная нагрузки на 1 м ригеля; l — пролет ригеля (между осями колонн).

Изгибающие моменты в стойках определяют как разность опорных моментов ригелей в узле путем распределения ее пропорционально погонным жесткостям стоек.

По полученным для различных возможных сочетаний постоянной и временной нагрузок моментам и поперечным силам строят объемлющую эпюру и производят перераспределение усилий (см. гл. 9). Если рама имеет более трех пролетов, то ее рассматривают как трехпролетную.

■ Расчет рам на горизонтальную (ветровую) нагрузку. Действующую на раму горизонтальную нагрузку заменяют сосредоточенными силами, приложенными к узлам рамы (рис. 12.6, б). В этом случае точки эпюры моментов стоек всех этажей, кроме первого, считают расположенными в середине высоты этажа, а в первом этаже (при защемленных в фундаментах стойках) — на расстоянии 2 h/3 от места защемления (рис. 12.6, г).

Ярусная поперечная сила Q_i равна сумме горизонтальных вышерасположенных сил:

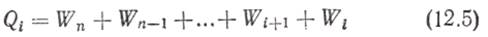
и распределяется между отдельными стойками яруса (этажа) пропорционально их жесткостям:

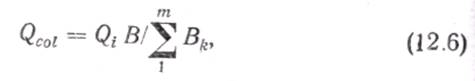
где В — жесткость рассматриваемой стойки i-го яруса; m — число стоек i-го яруса.

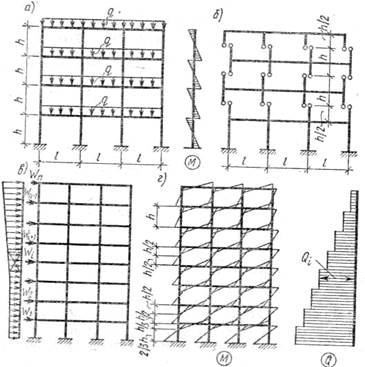
Рис. 12.6. К расчету многоэтажных рам на вертикальные (а, б) и

горизонтальные (в, г) нагрузки: Q_i — поперечная сила i-го яруса

Крайние стойки рамы имеют меньшую степень защемления в узле, чем средние, поэтому воспринимают меньшую долю ярусной поперечной силы. Это учитывается специальным коэффициентом β<1 [13].

Найдя поперечные силы, вычисляют изгибающие моменты в стойках всех этажей, кроме первого:

а для первого этажа моменты в стойке в верхнем M_t и нижнем М_b сечениях:

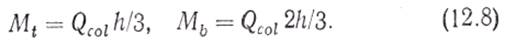
Опорные моменты в ригелях определяют из условия равновесия узлов.

По полученным для различных загружений (постоянными и временными нагрузками) эпюрам изгибающих моментов и поперечных сил строят объемлющие эпюры, производят перераспределение усилий в ригелях вследствие пластических деформаций и по полученным усилиям ведут расчет сечений колонн и ригелей. Ригели рассчитывают как изгибаемые элементы по нормальным и наклонным сечениям, колонны — как внецентренно сжатые элементы на действие изгибающего момента и соответствующей ему продольной силы.

■ Определение перемещений рамы от горизонтальной нагрузки. Помимо расчета прочности многоэтажных зданий требуется проверка горизонтального смещения верха здания от ветровой нагрузки, которое не должно превышать ¹/₁₀₀₀ высоты здания. Исследования показали, что горизонтальные перемещения многоэтажной рамы при отношении высоты здания к его ширине H/b<4 вызываются главным образом общей сдвиговой деформацией здания вследствие взаимного смещения концов стоек — перекосов этажей (рис. 12.7). Углы перекоса ψ=c/h (где с — линейный перекос, а h — высота этажа) могут быть приняты равными для всех стоек одного этажа. Для упругой рамы монотонной структуры, т. е. имеющей одинаковую во всех этажах погонную жесткость стоек и ригелей, угол перекоса i-го яруса.

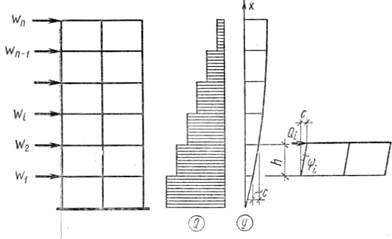
Рис. 12.7. К определению перемещений в рамной системе

где Q_i — сдвигающая сила, представляющая в данном случае ярусную поперечную силу Q_i [см. формулу (12.5)]; К — сдвиговая жесткость многоэтажного рамного каркаса, K=h/c, для монотонных рам с = (h²/12)×(1/s+l/r); s и r — суммы соответственно погонных жесткостей стоек и ригелей этажа.

При числе этажей больше 5 расположение ригелей можно считать непрерывным по высоте. Тогда непрерывными будут нагрузка w(x), поперечная сила Q_fr(x), перемещение у(х). Угол перекоса будет представлять собой тангенс угла наклона касательной к линии прогибов:

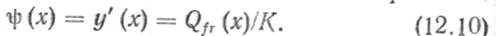
Интегрируя (12.10), получим выражение для прогиба здания на любой высоте х:

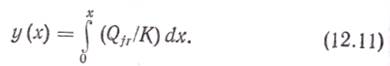
Используя зависимостьQ = w(H—х) для поперечной силы от равномерно распределенной нагрузки w(x) = w, получим из (12.11) прогиб верха здания

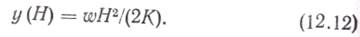
■ Расчет рамно-связевых и связевых систем. Эти системы в расчетном отношении оказываются сложнее рамных, что обусловлено наличием разнородных по характеру работы вертикальных несущих элементов (сплошных и проемных диафрагм, рам) и многообразием связей между ними, большей этажностью зданий, в ряде случаев асимметрией плана здания и расположения диафрагмы или ядер жесткости и т. п. Расчет таких систем в настоящее время ведут в предположении упругой работы железобетона.

В качестве основы для расчетов (в том числе на ЭВМ) рассматриваемых типов зданий используют расчетные модели, учитывающие наиболее важные особенности конструктивной схемы.

Наибольшее распространение в нашей стране и за рубежом получила дискретно-континуальная модель [17], согласно которой несущая система здания представляется в виде пучка вертикальных отдельных (дискретных) элементов (столбов), соединенных между собой непрерывно распределенными по высоте (континуальными) связями. Под столбами понимают сплошные диафрагмы, простенки проемных диафрагм, колонны в зданиях рамно-связевой системы и т. п. Роль связей играют перекрытия, перемычки в проемных диафрагмах, сварные соединения и т. п. Исследования показали, что при количестве этажей более 5 перекрытия, перемычки и другие связи можно считать непрерывными, как бы «размазанными» по высоте здания. Столбы и связи сопротивляются изгибу, сдвигу и осевым усилиям. Заделка вертикальных элементов может приниматься жесткой или упругоподатливой. Применение дискретно-континуальной модели позволяет свести задачу о расчете здания к системе линейных дифференциальных уравнений с постоянными коэффициентами. Число уравнений равно количеству швов между столбами. Уравнения могут быть составлены относительно перемещений, изгибающих моментов, продольных или поперечных сил в столбах, а также перерезывающих сил в связях и т. п.

Как уже отмечалось, расчет несущих систем, в том числе и на основе дискретно-континуальной модели, производят, как правило, на ЭВМ. Однако в практике проектирования для отдельных типов зданий возможны упрощения, позволяющие применять и ручной счет. Например, в симметричных зданиях с жесткими в своей плоскости перекрытиями (обеспечивающими одинаковое горизонтальное перемещение всех вертикальных элементов) плоскопараллельную несущую систему (рис. 12.8, а), образованную только рамами и сплошными диафрагмами, заменяют обобщенной рамно-связевой системой (рис. 12.8, б). При этом жесткость расчетной диафрагмы принимают равной сумме жесткостей вертикальных диафрагм одного направления, а жесткость рамы — суммарной жесткости всех ригелей и стоек рам каркасов того же направления.

Расчетные зависимости для рамно-связевой системы (рис. 12.8, а) получим, составив уравнения равновесия поперечных сил в вертикальных элементах [23]:

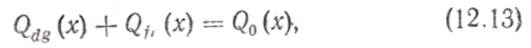
где Q_dg — поперечная сила, воспринимаемая диафрагмой; Q_fr — то же, рамой; Q_o — поперечная сила от внешней нагрузки, определяемая как в консольной балке.

Поперечная сила Q_fr связана с прогибом здания у формулой (12.11), а сила Q_dg — известной из сопротивления материалов зависимостью для сплошного стержня

Q_dg = -B_dgy"', (12.14)

где B_dg — жесткость расчетной сплошной диафрагмы.

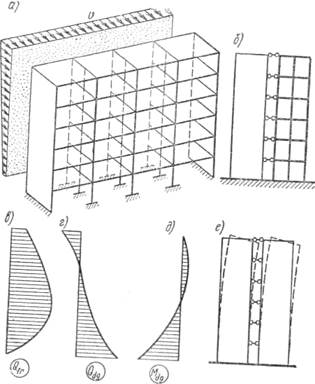
Рис. 12.8. К расчету рамно-связевых и связевых систем

Из (12.13) с учетом (12.10) и (12.14) получают

B_dgy"'-Ky' + Q₀ = 0. (12.15)

Дифференцируя, получают

B_dgу"" - Ку" — w(x) = 0. (12.16)

Вводя приведенные перемещения y₁=B_dgy и произведя преобразования, получают окончательное уравнение для плоской рамно-связевой системы [23]:

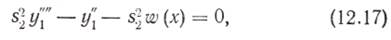
где s₂= .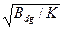

Решение уравнения (12.17) имеет вид

y₁ = А₁ + A₂s₂φ + A₃chφ + A₄shφ + y_1,p, (12.18)

где φ=x/s₂ — безразмерная координата; y_1,р — частное решение, зависящее от вида нагрузки, при равномерно распределенной нагрузке y_1,p=—ws 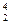φ²/2.

Производные постоянные A₁ A₂, A₃, A₄ находят из граничных условий:

y₁(0)=0, у₁"(λ) = 0, (12.19)

y'₁(0)=0, y'₁(λ)/s 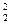-y'''₁(λ)=0

Из формулы (12.18) получают выражение для перемещения, которое для w(x) =w будет иметь вид

y₁ = ws 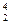(λφ — φ²/2 + ٕxchφ - λshφ - х), (12.20)

где λ=H/S₂ — характеристика жесткости здания; x = (l+λshλ)/(chλ).

Имея выражение для прогиба, легко получить формулы для усилий в раме и диафрагме:

Q_fr=y'₁/s 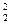; Q_dg=- y'''₁

M_dg=-y"₁. (12.21)

Из рис. 12.8, в...д видно, что в отличие от рамной системы Q_fr уменьшается в основании до нуля вследствие разгружающего действия диафрагм. По найденному распределению Q_fr могут быть вычислены изгибающие моменты в стойках и ригелях по аналогии с рамными системами. Значения M_dg и Q_dg непосредственно используются для расчета сечений диафрагм.

Прогиб верха здания на основании (12.20)

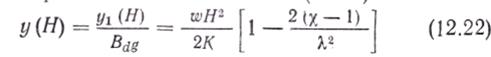
меньше соответствующего прогиба (12.12) рамной системы.

Для высоких зданий (H/b>4) необходимо учитывать изгибающий момент M = Nb, возникающий вследствие Продольных деформаций колонн. В этом случае при со­ставлении уравнения равновесия поперечных сил необходимо учесть дополнительный угол поворота, вызванный этим фактором [23].

Расчет связевых систем, приводящихся к плоскопараллельным, может быть также выполнен с использованием уравнения (12.16), причем в системах с глухими диафрагмами расчетное уравнение получим, если опустим в выражении (12.16) член, характеризующий сопротивление рамной части:

Полученная формула представляет известное из сопротивления материалов уравнение изгиба стержня (в данном случае консольного). Такой же результат можно получить при использовании консольной модели (рис. 12.8, е), являющейся частным случаем дискретно-континуальной и отражающей тот факт, что перекрытия с вертикальными элементами соединены шарнирно. Сопоставление результатов расчетов на основе дискретно-континуальной модели с более точными методами, а также с экспериментами на упругих моделях показывает, что эти результаты обеспечивают достаточную точность в зонах больших усилий, которые и являются определяющими при подборе сечений.

Существует также другая группа методов, базирующихся на так называемых дискретных расчетных моделях. Это метод стержневой аппроксимации и метод конечных элементов. При расчете по методу стержневой аппроксимации сплошные участки стен заменяют стержневой решеткой, а по методу конечных элементов — треугольными или прямоугольными конечными (т. е. малыми) элементами. Решение по обоим методам сводится к системе алгебраических уравнений, число которых зависит от числа узлов заменяющей модели. Точность решения повышается с уменьшением размеров элементов, однако одновременно увеличивается число узлов и порядок системы уравнений; для получения удовлетворительных результатов требуются ЭВМ с большим объемом памяти и высоким быстродействием. Поэтому дискретные модели целесообразно использовать для уточнения расчетных усилий и деформаций (в зонах концентрации напряжений, резкого изменения жесткости элементов и т. д.).

■ Расчет панельных зданий. Многоэтажные панельные здания представляют собой пространственную систему, состоящую из отдельных пластин, ослабленных проемами и соединенных между собой податливыми связями. Расчет выполняют на основе пространственных или плоских расчетных схем. Пространственные расчетные схемы применяются в виде системы пластинок, составной системы тонкостенных стержней, призматических оболочек и т. п., соединенных между собой распределенными или сосредоточенными связями. Этот расчет является более точным, однако возможен лишь с применением ЭВМ. Наряду с пространственными для приближенных расчетов применяют плоские схемы, среди которых наибольшее распространение получила схема, в которой здание расчленяется на вертикальные несущие элементы (включающие наружные и внутренние стены), рассматриваемые как консольные стержни. Принимается, что стержни шарнирно соединены между собой связями, обеспечива­ющими совместность поперечных перемещений стержней.