Технология моделирования случайных факторов

Генерация псевдослучайных чисел (ПСЧ)

Имитационное моделирование ИС, как правило, предполагает необходимость учета различных случайных факторов — событий, величин, векторов (систем случайных величин), процессов.

В основе всех методов и приемов моделирования названных случайных факторов лежит использование случайных чисел, равномерно распределенных на интервале [0;1].

До появления ЭВМ в качестве генераторов случайных чисел применяли механические устройства — колесо рулетки, специальные игральные кости и устройства, которые перемешивали фишки с номерами, вытаскиваемые вручную по одной.

По мере роста объемов применения случайных чисел для ускорения их моделирования стали обращаться к помощи электронных устройств. Самым известным из таких устройств был электронный импульсный генератор, управляемый источником шума, разработанный широко известной фирмой RAND Corporation. Фирмой в 1955 г. была выпущена книга, содержащая миллион случайных чисел, сформированных этим генератором, а также случайные числа в записи на магнитной ленте. Использовались и другие подобные генераторы — например, основанные на преобразовании естественного случайного шума при радиоактивном распаде. Все эти генераторы обладают двумя недостатками:

§ невозможно повторно получить одну и ту же последовательность случайных чисел, что бывает необходимо при экспериментах с имитационной моделью;

§ технически сложно реализовать физические генераторы, способные длительное время выдавать случайные числа "требуемого качества".

В принципе, можно заранее ввести полученные таким образом случайные числа в память машины и обращаться к ним по мере необходимости, что сопряжено с понятными негативными обстоятельствами — большим (причем неоправданным) расходов ресурсов ЭВМ и затратой времени на обмен данными между долгосрочной и оперативной памятью.

В силу этого наибольшее распространение получили другие генераторы, позволяющие получать так называемые псевдослучайные числа (ПСЧ) с помощью детерминированных рекуррентных формул. Псевдослучайными эти числа называют потому, что фактически они, даже пройдя все тесты на случайность и равномерность распределения, остаются полностью детерминированными. Это значит, что если каждый цикл работы генератора начинается с одними и теми же исходными данными, то на выходе получаем одинаковые последовательности чисел. Это свойство генератора обычно называют воспроизводимостью последовательности ПСЧ.

Программные генераторы ПСЧ должны удовлетворять следующим требованиям:

§ ПСЧ должны быть равномерно распределены на интервале [0; 1] и независимы, т.е. случайные последовательности должны быть некоррелированы;

§ цикл генератора должен иметь возможно большую длину;

§ последовательность ПСЧ должна быть воспроизводима;

§ генератор должен быть быстродействующим;

§ генератор должен занимать малый объем памяти.

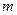Первой расчетной процедурой генерации ПСЧ, получившей достаточно широкое распространение, можно считать метод срединных квадратов, предложенный фон Нейманом и Метрополисом в 1946 г. Сущность метода заключается в последовательном нахождении квадрата некоторого -значного числа; выделении из него средних цифр, образующих новое число, которое и принимается за очередное в последовательности ПСЧ; возведении этого числа в квадрат; выделении из квадрата т средних цифр и т.д. до получения последовательности требуемой длины.

Как следует из описания процедуры метода, он весьма прост в вычислительном отношении и, следовательно, легко реализуем программно. Однако ему присущ очень серьезный недостаток — обусловленность статистических свойств генерируемой последовательности выбором ее корня (начального значения), причем эта обусловленность не является "регулярной", т.е. трудно определить заранее, можно ли использовать полученные данным методом ПСЧ при проведении исследований. Иными словами, метод срединных квадратов не позволяет по начальному значению оценить качество последовательности ПСЧ, в частности ее период.