Мультипликативный метод

Основная формула мультипликативного генератора для расчета значения очередного ПСЧ по значению предыдущего имеет вид:

,

где а, т — неотрицательные целые числа (их называют множитель и модуль).

Как следует из формулы, для генерации последовательности ПСЧ необходимо задать начальное значение (корень) последовательности, множитель и модуль, причем период (длина) последовательности Р зависит от разрядности ЭВМ и выбранного модуля, а статистические свойства — от выбранного начального значения и множителя. Таким образом, следует выбирать перечисленные величины так, чтобы по возможности максимизировать длину последовательности и минимизировать корреляцию между генерируемыми ПСЧ. В специальной литературе приводятся рекомендации по выбору значений параметров метода, использование которых обеспечивает (гарантирует) получение определенного количества ПСЧ с требуемыми статистическими свойствами. 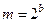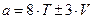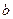Так, если для машины с двоичной системой счисления задать , , где — число двоичных цифр (бит) в машинном слове; Т — любое целое положительное число; V — любое положительное нечетное число, получим последовательность ПСЧ с периодом, равным 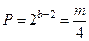. Заметим, что в принципе возможно за счет другого выбора модуля т увеличить длину последовательности до , частично пожертвовав скоростью вычислений. Кроме того, важно, что получаемые таким образом ПСЧ оказываются нормированными, т.е. распределенными от 0 до 1. От выбора корня последовательности ее длина не зависит (при равенстве остальных параметров).

Аддитивный метод

Основная формула для генерации ПСЧ по аддитивному методу имеет вид:

,

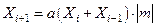где т — целое число.

Очевидно, что для инициализации генератора, построенного по этому методу, необходимо помимо модуля т задать два исходных члена последовательности. При 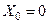; 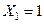последовательность превращается в ряд Фибоначчи. Рекомендации по выбору модуля совпадают с предыдущим случаем; длину последовательности можно оценить по приближенной формуле

.

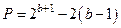Смешанный метод

Данный метод несколько расширяет возможности мультипликативного генератора за счет введения так называемого коэффициента сдвига с. Формула метода имеет вид:

.

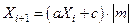За счет выбора параметров генератора можно обеспечить максимальный период последовательности ПСЧ .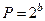

Разработано множество модификаций перечисленных конгруэнтных методов, обладающих определенными преимуществами при решении конкретных практических задач, а также рекомендаций по выбору того или иного метода. Для весьма широкого круга задач вполне удовлетворительными оказываются типовые генераторы ПСЧ, разработанные, как правило, на основе смешанного метода и входящие в состав стандартного общего программного обеспечения большинства ЭВМ. Специальным образом генерацию ПСЧ организуют либо для особо масштабных имитационных исследований, либо при повышенных требованиях к точности имитации реального процесса (объекта).

Подводя итог, подчеркнем, что разработка конгруэнтных методов зачастую осуществляется на основе эвристического подхода, основанного на опыте и интуиции исследователя. После модификации известного метода тщательно проверяют, обладают ли генерируемые в соответствии с новой формулой последовательности ПСЧ требуемым статистическими свойствами, и в случае положительного ответа формируют рекомендации по условиям ее применения.