Формализация вывода средствами логики высказываний
Для записи задачи на языке исчисления высказываний введем три логические переменные хк, хл, хп.
Истинное значение первой из них означает, что кот находится у левой комнаты, а ложное, что он находится у правой комнаты;
истинное значение переменной хл означает, что кусочек сыра лежит около левой комнаты, а ложное, что его там нет;
истинное значение переменной хп означает, что кусочек сыра лежит около правой комнаты, а ложное, что его там нет.
В результате таких обозначений табл. 3.1 можно заменить на табл. 3.2. Каждое состояние среды можно рассматривать как комбинацию (отношение) простейших свойств объектов, задаваемых значениями отдельных логических переменных. Так, состояние b1 соответствует комбинации свойств кота и кусочков сыра, состоящей в том, что кот находится в левой комнате, и в это же самое время около левой и правой комнат находится по кусочку сыра. На русском языке эту комбинацию можно выразить предложением: «Кот находится около левой комнаты, кусочек сыра лежит около левой комнаты и кусочек сыра лежит у правой комнаты». В соответствии с уже приведенной выше интерпретацией логических переменных хк, хл, хп это предложение можно представить формулой 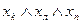 , которая истинна в единственном случае - все логические переменные, входящие в нее, истинны, т.е. среда находится в состоянии b1. Формулы такого типа, являющиеся конъюнкцией переменных с отрицанием или без него, называют элементарными конъюнкциями. Если среда находится в состоянии b2, то истинна формула
, которая истинна в единственном случае - все логические переменные, входящие в нее, истинны, т.е. среда находится в состоянии b1. Формулы такого типа, являющиеся конъюнкцией переменных с отрицанием или без него, называют элементарными конъюнкциями. Если среда находится в состоянии b2, то истинна формула 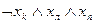 и т.д.
и т.д.
Элементарную конъюнкцию, в которую входит по одному разу каждая переменная, определяющую состояние среды, с отрицанием или без отрицания, называют полной конъюнкцией, или конституентой.
Аналогично тому, как были введены логические переменные хк, хл, хп, введем логические переменные z 1, z2, z3 для действий кота “Идти налево”, “Идти направо”, “Съесть “,соответственно. Переменная принимает истинное значение, если выполняется соответствующее ей действие. В противном случае она принимает ложное значение.
| Таблица 3.2 | ||||
| Состояние | Переменные | Формула, описывающая состояние | ||
| xk | xл | xп | ||
| b1 | И | И | И | 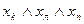
|
| b2 | Л | И | И | 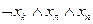
|
| b3 | И | И | Л | 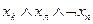
|
| b4 | Л | И | Л | 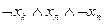
|
| b5 | И | Л | И | 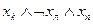
|
| b6 | Л | Л | И | 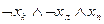
|
| b7 | И | Л | Л | 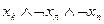
|
| b8 | Л | Л | Л | 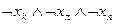
|
Для простоты будем полагать, что кот не может одновременно выполнять сразу более одного действия.
| Таблица 3.3 | |||
| Переход | Импликация, соответствующая переходу | ||
| Исходное состояние | Действие | Результирующее состояние | |
| b1 | c1 | b1 | 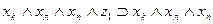
|
| b1 | c2 | b2 | 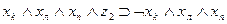
|
| b1 | c3 | b5 | 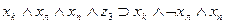
|
| b2 | c1 | b1 | 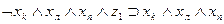
|
| b2 | c2 | b2 | 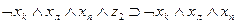
|
| b2 | c3 | b4 | 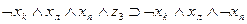
|
| b3 | c1 | b3 | 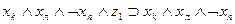
|
| b3 | c2 | b4 | 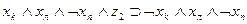
|
| b3 | c3 | b7 | 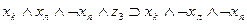
|
| b4 | c1 | b3 | 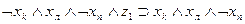
|
| b4 | c2 | b4 | 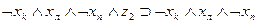
|
| b4 | c3 | b4 | 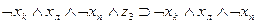
|
| b5 | c1 | b5 | 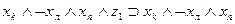
|
| b5 | c2 | b6 | 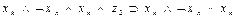
|
| b5 | c3 | b5 | 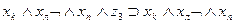
|
| b6 | c1 | b5 | 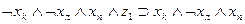
|
| b6 | c2 | b6 | 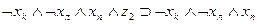
|
| b6 | c3 | b8 | 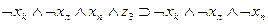
|
Рассмотрим теперь, как могут быть выражены в виде формул переходы среды из одного состояния в другое при совершении котом того или иного действия. Так, если кот находился в состоянии b1, и выполнил действие “Идти направо”, то среда перейдет в состояние b2 . Факт нахождения кота в состоянии b1, и выполнение им в это время действия “Идти направо” означает истинность формулы 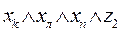 , а факт перехода состояния b1 при выполнении действия «идти направо» в состояние b2 будем интерпретировать как истинность формулы
, а факт перехода состояния b1 при выполнении действия «идти направо» в состояние b2 будем интерпретировать как истинность формулы 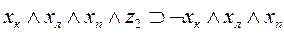 , что позволяет при истинности
, что позволяет при истинности 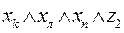 сделать заключение об истинности
сделать заключение об истинности 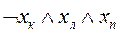 . Точно так же можно выразить в виде аналогичных формул все остальные переходы, показанные на рис. 3.2. Представим их в виде табл. 3.3. В первых трех столбцах этой таблицы указаны переходы, имеющиеся на рис. 3.2, а в последнем -формулы, соответствующие переходам.
. Точно так же можно выразить в виде аналогичных формул все остальные переходы, показанные на рис. 3.2. Представим их в виде табл. 3.3. В первых трех столбцах этой таблицы указаны переходы, имеющиеся на рис. 3.2, а в последнем -формулы, соответствующие переходам.
Поиск решения
Решения задачи для среды кота практически очевидны, когда построено дерево переходов состояний среды, по которому легко проследить пути, ведущие в целевые состояния из начального. В реальных задачах это дерево может быть очень большим, вследствие чего нецелесообразно использовать стратегию поиска, согласно которой необходимо сначала получать дерево целиком. Вместо этого используются другие более эффективные стратегии поиска, речь о которых пойдет в главе 4. Однако, какая бы из этих стратегий не применялась, элементарным шагом поиска является переход из одного состояния среды в другое и анализ состояния, в которое переход был осуществлен, на принадлежность к числу целевых. Каждый допустимый переход из состояния bi. после совершения действия сj в состояние bk можно задавать с помощью правила перехода: « Если среда находится в состоянии bi. и совершается действие сj, то она должна перейти в состояние bk».
Совокупность правил подобного типа используется в процессе поиска. Одной из очевидных, но чрезвычайно неэкономных стратегий поиска, позволяющей найти все решения для среды кота, может быть следующая.
1.Образовать множество В = {b1}, состоящее из одного начального состояния b1.
2. Для каждого состояния множества В и каждого действия с найти, согласно соответствующим правилам перехода, все состояния bk, в которые переходит среда. Совокупность всех таких состояний, за исключением тех, которые уже встречались в ранее образованных множествах В, принять за новое множество В.
3. Проверить, нет ли среди элементов этого множества целевых состояний. Если целевых состояний нет, то перейти к п. 2. Если целевые состояния есть, то выписать в порядке использования правил все последовательности действий, которые привели к целевым состояниям, удалить эти состояния из множества В и перейти к выполнению следующего пункта.
4. Проверить, все ли целевые состояния найдены. Если найдены все, то прекратить поиск. Если найдены не все, то перейти к п. 2.
Проиллюстрируем на примере среды кота применение этой стратегии. Правила перехода выписывать не будем, поскольку в нашем распоряжении уже есть дерево переходов (см. рис. 2.2).
Итак, вначале В={b1}. После выполнения п. 2 имеем совокупность состояний b1,b2,b5. В этой совокупности нет ни одного целевого состояния, а состояние b1 уже встречалось. Поэтому, согласно п. 3, принимаем В={b2,b5} и переходим к выполнению п.2. В результате получаем совокупность состояний b1,b2,b4,b5,b6, среди которых опять нет целевых, а b1,b2,b6 уже встречались. Поэтому В={b4,b6} и снова возвращаемся к п. 2. После очередного выполнения этого пункта имеем совокупность состояний b3,b4,b5,b6,b8. Среди этих состояний b4,b5,b6 уже встречались, а состояние b8, является целевым. В это состояние ведет единственная последовательность действий с3,c2,c3. Однако еще не все целевые состояния найдены, а именно не найдено состояние b7 . Поэтому в соответствии с п. 4 продолжим поиск, вновь переходя к п. 2 с множеством В = {b3}. В результате получим совокупность состояний b3, b4, b7, среди которых b3, b4 уже встречались, а b7 - целевое. Последовательностью действий, ведущих в состояние b7, является c2 c3 c1 c3. И так, все целевые состояния найдены, решение задачи в виде последовательности действий, ведущих в эти состояния, получено. Поиск на этом прекращается.
Дата добавления: 2016-01-09; просмотров: 889;
