Синтаксис логики высказываний
Синтаксис логики высказываний прост и имеет прямые синтаксические и семантические аналоги в естественных языках, что чрезвычайно облегчает нам понимание логики высказываний. Символами языка логики высказываний, составляющими ее алфавит, являются логические константы ИСТИНА и ЛОЖЬ, сокращенно обозначаемые буквами И и Л, логические переменные х, у, z, обозначаемые строчными буквами латинского алфавита, логические связки (И), (ИЛИ), (НЕ), ЭКВИВАЛЕНТНО, => (ВЛЕЧЕТ) и круглые скобки. Значениями логических переменных являются логические константы. Предложения языка логики высказываний, называемые также формулами или высказываниями, составляют в соответствии со следующими правилами:
Логические константы являются простыми предложениями;
Логические переменные также простые предложения;
Сложные предложения формируются из простых с помощью связок (И), (ИЛИ), (НЕ), (ЭКВИВАЛЕНТНО), => (ВЛЕЧЕТ);
Простые и сложные предложения, заключенные или не заключенные в скобки, являются предложениями языка логики высказываний;
Из предложений с помощью связок и скобок можно образовать новые предложения языка логики высказываний;
Связки имеют следующий порядок старшинства Ø,Ù,Ú,É,º т.е. связка Ø самая старшая, а связка º самая младшая.
Формулы логики высказываний, составленные по этим правилам, называют правильно построенными формулами или сокращенно формулами.
2.1.2. Семантика логики высказываний.
Семантику логики высказываний можно пояснить смысловой интерпретацией ее предложенийили формул, под которой обычно понимают процесс установления соответствия между логическими переменными и изменяющимися свойствами объектов среды и между значениями переменных (константами) и конкретными значениями свойств объектов. С помощью алгебры логики можно записывать любое правило и предложение для СИИ..
Пример 1. Студент, который не ходит на занятия и не занимается дома, не сдаст экзамен. Обозначим через x1 событие: ходить на занятия; через x2 событие – заниматься дома и через y – сдать экзамен. Тогда формальная запись на языке алгебры логике будет иметь вид:
`y=`x1 Ù`x2
Пример 2.Если истинно утверждение, что Иван и Мария являются родителями и Юры и Анны, то Юра и Анна являются братом и сестрой. Обозначим: x1 – Иван, x2 – Мария, x3 – Юра, x4 – Анна, y1 – родители Юры, y2 – родители Анны, y – Юра и Анна – брат и сестра.
y1=x1Ùx2, y2=x1Ùx2, y=y1Ùy2.
То же самое можно описать словами:
“Родители_Юры”=”Иван”Ù”Мария”
“Родители_Анны”=”Иван”Ù”Мария”
“Юра_и_Мария – брат_и_сестра”=”Родители_Юры”Ù”Родители_Анны”
Иначе говоря, интерпретация определяет семантику формул (предложений, высказываний) путем сопоставления переменных в формулах со свойствами объектов среды, а отношений между этими свойствами — с формулами. Это позволяет по значению формул после подстановки вместо переменных конкретных значений свойств судить о наличии или отсутствии у среды тех или иных совокупных свойств или отношений. Если дана какая-либо формула, то подстановка в формулу констант вместо ее переменных называется конкретизацией. Таким образом конкретизация является результатом интерпретации.
Будем полагать, что, употребляя формулу xÉy, мы вкладываем в нее смысл, вытекающий из следующего предложения: «Мы заявляем, что истинность высказывания «х влечет у» означает, что истинность х влечет истинность у, а больше мы ничего не заявляем».
Истинностные значения любой формулы, т.е. ее семантику, всегда можно задать таблицей, состоящей из двух частей: в левой части таблицы перечислены все наборы значений аргументов, а в правой соответствующие наборам значения формулы. Задание таких таблиц для связок облегчается тем, что значениями аргументов и формул являются только две величины – И или Л. Такие таблицы в логике высказываний называют таблицами истинности.
Если формула интерпретирована, то ее таблица истинности определяет семантику интерпретированной формулы, поскольку по ней можем всегда определить, какие же отношения между свойствами объектов, обозначаемых переменными, имеют место (формула истинна) и не имеют места (формула ложна).
С помощью алгебры логики можно записывать любое правило и предложение для СИИ.
2.1.3. Общезначимые формулы и их роль.
Формулы, истинные на всех наборах значений своих аргументов, называют общезначимыми формулами. Если какая-либо формула a является общезначимой, то этот факт обычно записывается с использованием знака общезначимости ½=  который ставится перед формулой: |=a. Проверку формулы на общезначимость можно осуществить с помощью таблицы истинности: если формула истинна во всех строках таблицы истинности, то эта формула общезначима. Рассмотрим, например, формулу ØxÙ(ØyÚy)ÉxØx. Из таблицы ясно, что формула является общезначимой, т.к. значения переменных в последнем столбце всегда истинно.
который ставится перед формулой: |=a. Проверку формулы на общезначимость можно осуществить с помощью таблицы истинности: если формула истинна во всех строках таблицы истинности, то эта формула общезначима. Рассмотрим, например, формулу ØxÙ(ØyÚy)ÉxØx. Из таблицы ясно, что формула является общезначимой, т.к. значения переменных в последнем столбце всегда истинно.
| x | y | Øx | Øy | ØxÚy | ØxÙ(ØyÚy) | ØxÙ(ØyÚy)ÉxØx |
Ранее было заявлено, что истинность высказывания a1Éa2 всегда означает, что истинность a1 влечет истинность a2 (здесь a1 и a2 являются формулами логики высказываний). Потому, установив факт общезначимости формулы a1Éa2 и истинности a1, всегда можно сделать заключение об истинности a2. Таким образом, общезначимость формул вида a1Éa2, называемых импликативными формулами, является важным свойством для получения заключения об истинности a2 , называемого заключением, при истинности a1, называемого посылкой. Для простоты импликативные формулы a1Éa2 будем называть так же, как и связку É, импликацией. В логике высказываний известно много общезначимых формул, называемых обычно законами логики высказываний. Наиболее известными являются следующие законы.
Коммутативные: x1Ùx2=x2Ùx1, x1Úx2=x2Úx1;
Дистрибутивные: x1Ù (x2 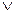 x3)=(x1Ùx2)Ú(x1Ùx3), x1Ú(x2Ùx3)=(x1Úx2)Ù(x1Úx3);
x3)=(x1Ùx2)Ú(x1Ùx3), x1Ú(x2Ùx3)=(x1Úx2)Ù(x1Úx3);
Ассоциативные: x1Ù(x2 Ùx3)=(x1Ùx2)Ùx3, и x1Ú(x2Úx3)=(x1Úx2)Úx3;
законы Де Моргана:
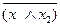 =
= 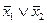 ,
, 
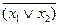 =
=  ,
,
закон двойного отрицания: 
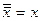 .
.
Кроме того, справедливы следующие соотношения:
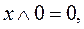
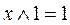 ,
, 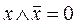 .
. 
 ,
, 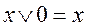 ,
, 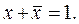
Сложные формулы, как правило, можно упростить. Для этого можно использовать следующие эквивалентности:
 – правила поглощения,
– правила поглощения,
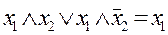 – правило склеивания,
– правило склеивания, 
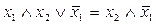 – правило вычеркивания.
– правило вычеркивания.
Их доказательства осуществляются путем построения соответствующих таблиц истинности.
Рассмотрим пример упрощения логической функции. Пусть

Последовательное применение приведенных выше правил дает:
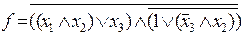 =
= 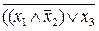
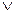

 =
=
=( 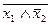
 )
) 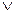
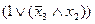 =(
=( 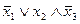 )
)  =1.
=1.
Кроме общезначимых, существуют формулы выполнимые и невыполнимые. Формула называется выполнимой, если существуют наборы значений ее аргументов, на которых она принимает истинное значение, и наборы значений, на которых она принимает ложное значение.
Если формула на всех наборах значений ее аргументов принимает ложное значение, то она называется невыполнимой.
Установление истинности следствия по общезначимой импликативной формуле достаточно универсальный способ для вывода заключений, но требует проверки общезначимости последней. Если формула a1 É a2 не является общезначимой, то подобного заключения делать нельзя.
Проверку общезначимости можно осуществить с помощью таблицы истинности. Однако построение таблиц истинности слишком трудоемко для того, чтобы можно было решать реальные задачи. Вместо этого используют специальные правила вывода, применение которых базируется не на понятии общезначимости формулы, в частности общезначимости импликативной формулы, а на понятии модели формулы.
Нечеткие множества
Записывая и решая задачу на языке исчисления высказываний или предикатов, мы получаем ответ в виде «да» или «нет»,(истина или ложь, 0 или 1). Однако во многих задачах мы не уверены в исходных данных, мы знаем их приближенно и поэтому удовлетворимся приближенным ответом.
Для математического решения таких задач используется нечеткая логика, предложенная американским математиком Л. Заде в начале 60-х годов.
Обычная логика, в которой есть два логических значения ИСТИНА и ЛОЖЬ, связана с таким же четким разделением объектов на два множества. Например, логическое условие
ПРИЗЫВНИК = ((ПОЛ = МУЖСКОЙ) Ù (ВОЗРАСТ>ПРИЗЫВНОЙ))
 подразумевает разделение людей по признаку пола МУЖСКОЙ/ЖЕНСКИЙ и по возрасту ВОЗРАСТ>ПРИЗЫВНОЙ/ ВОЗРАСТ<ПРИЗЫВНОЙ. Логическая операция конъюнкции описывает ПРИЗЫВНИКА как пересечение множеств:
подразумевает разделение людей по признаку пола МУЖСКОЙ/ЖЕНСКИЙ и по возрасту ВОЗРАСТ>ПРИЗЫВНОЙ/ ВОЗРАСТ<ПРИЗЫВНОЙ. Логическая операция конъюнкции описывает ПРИЗЫВНИКА как пересечение множеств:
Рис.2.1.Операция пересечения множеств
Вместе с тем во многих случаях приходится иметь дело с не столь определенными понятиями. Например, выражение МОЛОДОЙ ЧЕЛОВЕК не указывает точно ни на какой возраст. Правда, можно отметить, что возраст 10 лет под понятие МОЛОДОГО ЧЕЛОВЕКА. по-видимому, не подпадает, точно так же, как и возраст 50 лет. Однако точно указать диапазон возраста МОЛОДОГО ЧЕЛОВЕКА в виде условия
МОЛОДОЙ ЧЕЛОВЕК=((ВОЗРАСТ>МИНИМАЛЬНЫЙ) И (ВОЗРАСТ< МАКСИМАЛЬНЫЙ)) невозможно – множество возрастов, подпадающих под понятие МОЛОДОГО ЧЕЛОВЕКА, является нечетким.
Если считать, что принадлежность объекта множеству описывается функцией принадлежности, принимающей значения от 0 до 1, то разница между обычными (четкими) и нечеткими множествами состоит в следующем. Для четкого множества функция принадлежности принимает значения только 0 и 1.
Например, функция принадлежности к призывному возрасту P(y) имеет вид (рис.2.2). В случае же нечеткого множества функция принадлежности принимает и промежуточные значения. Например, функция принадлежности к множеству МОЛОДОЙ ЧЕЛОВЕК может иметь вид (рис.2.3).
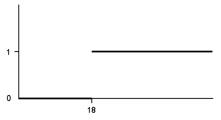 |
Рис.2.2. Функция принадлежности четкого множества.
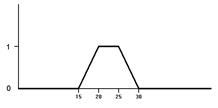 |
Рис.2.3. Функция принадлежности нечеткого множества
и в таком случае описывается формулами:
при y<15 P(y)=0;
при 15<y<20 P(y)=(y-5)/5;
при 20<y<25 P(y) = 1;
при 25<y<30 P(y)=(30-y)/5;
при y>30 P(y) = 0.
Иными словами, при возрасте менее 15 и старше 30 лет человек молодым заведомо не является, а в промежутке от 20 до 25 лет - заведомо является. В промежутке от 15 до 20 лет статус МОЛОДОГО ЧЕЛОВЕКА плавно возрастает, принимая значения от 0 до 1, а в промежутке от 25 до 30 лет - убывает от 1 до 0.
Для того, чтобы описать нечеткое множество МОЛОДОЙ ЧЕЛОВЕК, следует указать все его элементы с указанием степени принадлежности элемента множеству. Это делается с помощью записи
МЧ=0.2/16+0.4/17+0.6/18+0.8/19+1/20+1/21+1/22+1/23+1/24+1/25+0.8/26+0.6/27+0.4/28+0.2/29
В тех случаях, когда это не может привести к путанице, можно использовать обычное обозначение коэффициентов, принятое в алгебре. Например, если множество Z состоит из элементов a, b, c, d, e с функцией принадлежности
Z = 0.1/a+0.5/b+0.9/c+0.7/d+0.5/e
это может быть также записано во форме
Z = 0.1a+0.5b+0.9c+0.7d+0.5e
2.2.1. Операции с нечеткими множествами.
К нечетким множествам, как и к четким, применимы операции объединения, пересечения и дополнения. Если считать, что в универсальном множестве U выделены два нечетких множества A и B с функциями принадлежности f и g, то их объединение имеет функцию принадлежности h
h(u) = max (f(u), g(u))
Например, если
U = (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)
A = 0.8/0+0.7/1+0.6/2+0.4/3+0.2/4+0.1/5+0.1/6+0.1/7
B = 0.1/3+0.3/5+0.5/7+0.7/8+0.9/9
то A È B имеет вид
A È B = 0.8/0+0.7/1+0.6/2+0.4/3+0.2/4+0.3/5+0.1/6+0.5/7+0.7/8+0.9/9
 |
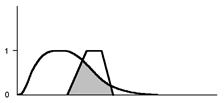
Аналогично, функция принадлежности для пересечения нечетких множеств A и B имеет вид min (f(u), g(u)). В том же примере
A Ç B = 0.1/3+0.1/5+0.1/7
Дополнение множества имеет функцию принадлежности, вычисляемую как дополнение до 1 функции принадлежности исходного множества. Так, дополнение множества A имеет функцию принадлежности
ØA = 0.2/0+0.3/1+0.4/2+0.6/3+0.8/4+0.9/5+0.9/6+0.9/7+1/8+1/9
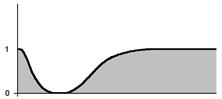 |
Легко заметить, что если множества являются четкими, т.е. функция принадлежности принимает только значения 0 и 1, то построенные указанным образом функции принадлежности описывают обычные операции объединения, пересечения и дополнения множеств.
 |
НЕЧЕТКАЯ ЛОГИКА
В отличие от обычной логики, где существуют только два значения истинности утверждения ИСТИНА и ЛОЖЬ, в нечеткой логике "значение истинности" утверждения может принимать и промежуточные значения. Считается, что ИСТИНА имеет значение 1, ЛОЖЬ - 0, и истинность любого утверждения u, обозначаемая m(u), находится в промежутке между этими значениями.
В нечеткой логике существуют те же логические операции конъюнкции, дизъюнкции и отрицания, однако они определяются иначе, чем в обычной логике. Если истинность логических операций конъюнкции, дизъюнкции и отрицания в обычной логике задается таблицами истинности, то в нечеткой логике она задается формулами. Если истинность утверждения u равна m(u), а v - m(v), то истинность конъюнкции, дизъюнкции и отрицания выражается формулами
m(uÙv) =min(m(u), m(v)), m(u Ú v) = max (m(u), m(v))
m(Øu) = 1-m(u)
При этом свойства нечетких операций в значительной степени сходны со свойствами операций в обычной логике, в частности:
m(uÙv)=m(vÙu), m(uÚv)=m(vÚu)
m((uÙv)Ùw)=m(uÙ(vÙw)), m((uÚv)Úw)=m(uÚ(vÚw))
m(Ø(Øu))=m(u), m(Ø(uÙv))=m(ØuÚØv)
m(Ø(uÚv))=m(ØuÙØv), m((uÚv)Ùw)=m((uÙw)Ú(vÙw))
m((uÙv)Úw)=m((uÚw) (v Ú w)), m(0Úu)=m(u)
m(1Úu)=1, m(0Ùu)=0, m(1Ùu)=m(u)
(Однако аналогия не является полной - например, аналоги формул uÙØu=0 и uÚØu=1 в нечеткой логике неверны.)
Используемые в логическом выводе формулы импликации вида A É B также могут быть нечеткими, т.е. их уровень истинности может быть меньше 1. В этом случае уровень истинности заключения вычисляется как произведение уровня истинности посылки на уровень истинности импликации. Например, если m(A)=0.9, а m(AÉB) = 0.8, то m(B)=0.72.
Вопросы для самопроверки к главе 2:
1.Могут ли системы искусственного интеллекта создаваться на одном из алгоритмических языков, например Бейсике?
2.Каким образом на языке исчисления высказываний можно записать выражение «студент должен сдать экзамены по математике и физике или по литературе и истории»?
3.Может ли функция принадлежности быть равна 3?
4.Сколько функций трех переменных существует в исчислении высказываний?
5. Запишите функцию эквивалентности через функции конъюнкции, дизъюнкции и отрицания.
Тесты к главе 2
1.Исчисление высказываний оперирует
А) с троичными переменными, Б) с двоичными переменными,
В) с однозначными переменными.
2. Свойства исчисления высказываний доказываются с помощью
А) логического вывода ,Б) таблиц истинности, В) формул.
3.Число логических функций
А) бесконечно, Б) конечно, но не зависит от числа аргументов
В) зависит от числа аргументов.
4.Логическое сложение двух единиц равно
А) нулю, Б) двум, В) единице.
5.Функция принадлежности объединения двух нечетких множеств равна
А) максимуму функции принадлежности каждого множества
Б) функции принадлежности одного из множеств
В) минимуму функции принадлежности каждого множества.
Глава 3. Логические рассуждения.
Рассуждением или умозаключением обычно называют ряд мыслей, изложенных в логически последовательной форме.
Агент должен уметь находить интересующие его состояния среды (целевые состояния), если он что-либо знает о других ее состояниях. Определение целевых состояний осуществляется с помощью поиска или рассуждений в пространстве состояний.
Дата добавления: 2016-01-09; просмотров: 1896;
