Расчет статически неопределимой стержневой конструкции, работающей на растяжение-сжатие (задача № 5)
Условие задачи
Стержневая конструкция, состоящая из абсолютно жесткого диска и двух деформируемых стержней длиной l1 и l2, соединенных шарнирами, подвержена действию силы F (рис. 1.11). Примем следующие исходные данные: 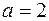 м,
м, 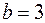 м,
м, 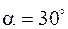 ,
,  ,
, 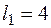 м,
м,  м.
м.
 Рис. 1.11. Схема конструкции в задаче № 5
Рис. 1.11. Схема конструкции в задаче № 5
|
Задача состоит из трех частей:
Часть 1. Расчет по упругой стадии деформации. В зависимости от исходных данных, выписанных из таблицы и являющихся индивидуальными для каждого студента, надо либо определить грузоподъемность конструкции, либо подобрать размеры поперечного сечения расчетом по допускаемым напряжениям.
Часть 2. Расчет по предельному пластическому состоянию. Требуется найти грузоподъемность (или подобрать сечения стержней) расчетом по предельному состоянию.
Часть 3. Определение дополнительных напряжений, связанных с изменением температуры на DT или неточностью изготовления D одного из стержней. Допустим, что в рассматриваемой задаче стержень 1 охлаждается (DT1 < 0), и найдем возникающие в стержнях конструкции температурные напряжения.
Решение
Прежде всего убедимся, что рассматриваемая конструкция является статически неопределимой. Сосчитаем число неизвестных: ими являются продольные силы в двух деформируемых стержнях и две опорные реакции в шарнирно неподвижной опоре в точке А. Таким образом, имеем 4 неизвестные, а число независимых уравнений статики для данной системы равно 3. Система является один раз статически неопределимой.
Часть 1. Для расчета конструкции по упругой стадии деформации необходимо составить три группы уравнений:
* уравнения равновесия;
* уравнения совместности деформаций;
* физические уравнения (закон Гука).
Чтобы составить уравнения равновесия, нарисуем план сил. Для этого рассечем стержни и, отбросив части стержней, заменим их внутренними усилиями – продольными силами N1 и N2 (рис. 1.12, а). Важно, чтобы на плане сил направления усилий соответствовали плану перемещений. Для того, чтобы выяснить как направлены продольные силы в стержнях, нарисуем приближенный план перемещений (рис. 1.12, б), пользуясь принципами, описанными при решении задачи № 3. Точки В и С жесткого диска поворачиваются с радиусами AB и АС вокруг неподвижной точки А на один и тот же угол g и перемещаются по дугам, которые заменяем перпендикулярами 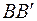 и
и  Для того, чтобы найти абсолютные деформации стержней, надо из точек
Для того, чтобы найти абсолютные деформации стержней, надо из точек 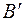 и
и 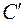 (новые положения узлов В и С) опустить перпендикуляры на направления стержней. Как видно из рис. 1.12, б стержень 1 укорачивается на
(новые положения узлов В и С) опустить перпендикуляры на направления стержней. Как видно из рис. 1.12, б стержень 1 укорачивается на 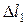 (выделенный жирным отрезок), и поэтому на плане сил усилие N1 показано сжимающим. Стержень 2 согласно плану перемещений удлиняется на
(выделенный жирным отрезок), и поэтому на плане сил усилие N1 показано сжимающим. Стержень 2 согласно плану перемещений удлиняется на 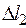 , и на рис. 1.12, а продольная сила N2 нарисована растягивающей.
, и на рис. 1.12, а продольная сила N2 нарисована растягивающей.
 Рис. 1.12. К решению задачи № 5:
а – план сил от действия F;
б – план перемещений от действия F
Рис. 1.12. К решению задачи № 5:
а – план сил от действия F;
б – план перемещений от действия F
|
Теперь составим три уравнения равновесия:
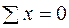 ;
; 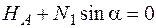 ;
;
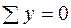 ;
; 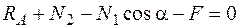 ;
;
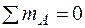 ;
; 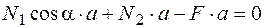 .
.
Запишем вторую группу уравнений – уравнения совместности деформаций. Поскольку данная система является один раз статически неопределимой, необходимо составить одно уравнение совместности деформаций. Это геометрическое уравнение, связывающее абсолютные деформации стержней, и его мы получим на основании плана перемещений. Из подобия треугольников ABB¢ и ACC¢ на рис. 1.12, б 
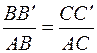 . Связывая отрезки BB¢ и CC¢ с деформациями стержней
. Связывая отрезки BB¢ и CC¢ с деформациями стержней 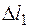 и
и  и учитывая, что AB = a,а
и учитывая, что AB = a,а 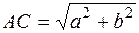 , получим уравнение совместности деформаций
, получим уравнение совместности деформаций
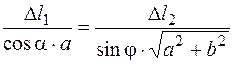 .
.
Поскольку 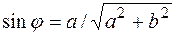 , то окончательно
, то окончательно
 .
.
Это уравнение показывает, во сколько раз абсолютное удлинение второго стержня больше абсолютного укорочения первого стержня. При построении плана перемещений в масштабе (что рекомендуется) результаты вычислений можно проверить по рисунку, измерив отрезки 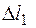 и
и 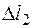 и найдя их отношение.
и найдя их отношение.
Теперь надо связать деформации стержней с внутренними усилиями. Предполагая, что материал подчиняется закону Гука (расчет по упругой стадии деформаций), запишем третью группу уравнений
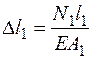 и
и 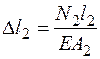 .
.
Мы получили полную систему уравнений для определения всех неизвестных (  ). Как правило, нас интересуют только продольные силы в стержнях, поэтому из уравнений равновесия при решении системы используется только последнее уравнение, в которое не входят опорные реакции. Решая полученную систему уравнений, найдем внутренние усилия в стержнях:
). Как правило, нас интересуют только продольные силы в стержнях, поэтому из уравнений равновесия при решении системы используется только последнее уравнение, в которое не входят опорные реакции. Решая полученную систему уравнений, найдем внутренние усилия в стержнях:
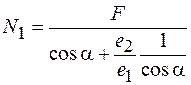 ;
;
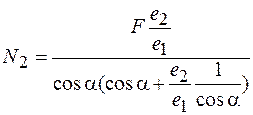 .
.
Здесь введено обозначение 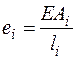 – погонная жесткость i-го стержня.
– погонная жесткость i-го стержня.
Заметим, что, как видно из полученных формул, усилия зависят не только от величины нагрузки и геометрических размеров конструкции, как в статически определимых системах, но и от отношения погонных жесткостей стержней. Эта важная закономерность справедлива для любой статически неопределимой конструкции и позволяет влиять на распределение усилий в стержнях без изменения ее геометрической схемы. Для принятых в данной задаче исходных данных получим  и
и 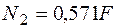 .
.
Определив внутренние усилия в стержнях, находим напряжения и выбираем наиболее напряженный стержень. Из условия прочности этого (наиболее напряженного) стержня либо определяем допускаемую нагрузку, либо подбираем размеры поперечных сечений стержней (заданное отношение площадей сечения необходимо сохранить). Напряжения в стержнях 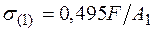 ,
, 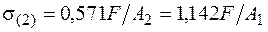 . Из сравнения видно, что наиболее напряженным является стержень 2. Из условия прочности этого стержня
. Из сравнения видно, что наиболее напряженным является стержень 2. Из условия прочности этого стержня
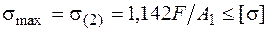
находим либо значение F, либо А1 (А2 по заданному отношению равно А1/2).
Для проверки рекомендуем после определения допускаемой нагрузки (либо размеров площадей сечения) еще раз найти напряжения в стержнях и убедиться в том, что условие прочности выполняется в обоих стержнях.
Часть 2. Сделаем расчет конструкции по предельному пластическому состоянию. Поскольку заданная система является один раз статически неопределимой, то в предельном состоянии должны потечь два стержня, то есть все деформируемые стержни конструкции. Для определения предельной нагрузки нарисуем план сил в предельном состоянии (рис. 1.13). Направления усилий снова должны соответствовать плану перемещений. Составим одно уравнение равновесия в предельном состоянии (такое уравнение, в которое не входят неизвестные опорные реакции):
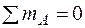 ;
; 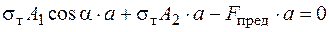 .
.
Из этого уравнения можно найти значение предельной нагрузки. Для конкретных исходных данных, использованных в первой части задачи, получим:
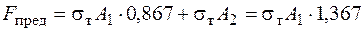 .
.
 Рис. 1.13. План сил в предельном состоянии
Рис. 1.13. План сил в предельном состоянии
|
Из условия прочности конструкции по предельному состоянию 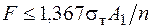 либо находим значение допускаемой нагрузки, либо подбираем размер А1.
либо находим значение допускаемой нагрузки, либо подбираем размер А1.
Сравним величины допускаемых нагрузок, найденных разными методами для рассмотренного примера. Допускаемая нагрузка, определенная расчетом по упругой стадии деформации
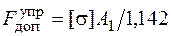 ,
,
оказалась меньше допускаемой нагрузки, полученной расчетом по предельному пластическому состоянию 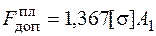 , на 56%.
, на 56%.
Часть 3. Найдем дополнительные напряжения в стержнях конструкции, связанные с охлаждением стержня 1 на 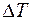 градусов. Предполагая, что в процессе деформации материал стержней остается упругим, расчет ведем по той же схеме, что и в первой части задачи, т. е. составляем три группы уравнений:
градусов. Предполагая, что в процессе деформации материал стержней остается упругим, расчет ведем по той же схеме, что и в первой части задачи, т. е. составляем три группы уравнений:
* уравнения равновесия;
* уравнения совместности деформаций;
* физические уравнения.
Уравнения равновесия составляем по плану сил (рис. 1.14, а), уравнения совместности деформаций – по плану перемещений (рис. 1.14, б). План сил и план перемещений, как и раньше, должны соответствовать друг другу. Поясним особенности построения плана перемещений от температурного воздействия. Если бы конструкция была статически определимой, т. е. стержень 2 отсутствовал, то стержень 1 при охлаждении уменьшил бы свою длину на величину 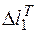 , жесткий диск повернулся бы на угол g¢ и узел В переместился в положение В¢¢. Поскольку конструкция статически неопределима, то лишний стержень 2 препятствует такой деформации. В результате жесткий диск повернется только на угол g, точка В перейдет в положение В¢. Стержень 1 окажется растянутым на величину
, жесткий диск повернулся бы на угол g¢ и узел В переместился в положение В¢¢. Поскольку конструкция статически неопределима, то лишний стержень 2 препятствует такой деформации. В результате жесткий диск повернется только на угол g, точка В перейдет в положение В¢. Стержень 1 окажется растянутым на величину 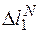 (выделенный жирным отрезок на плане перемещений рис. 1.14, б) и в нем возникнет растягивающее усилие N1. В свою очередь стержень 2 в процессе деформации также будет растянут на величину
(выделенный жирным отрезок на плане перемещений рис. 1.14, б) и в нем возникнет растягивающее усилие N1. В свою очередь стержень 2 в процессе деформации также будет растянут на величину 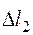 продольной силой N2. В соответствии с планом перемещений на плане сил (см. рис. 1.14, а) оба стержня показаны растянутыми.
продольной силой N2. В соответствии с планом перемещений на плане сил (см. рис. 1.14, а) оба стержня показаны растянутыми.
| Рис. 1.14. К решению задачи № 5: а – план сил от температурного воздействия; б – план перемещений от температурного воздействия |
Теперь запишем систему уравнений для определения внутренних усилий в заданной конструкции:
уравнение равновесия
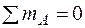 ;
; 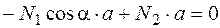 ;
;
уравнение совместности деформации [3]
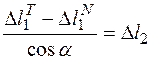
и физические уравнения
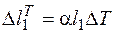 ;
; 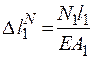 ;
; 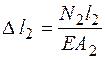 .
.
Решая эту систему уравнений, найдем усилия в стержнях системы, а далее по формуле (1.1) температурные напряжения. Заметим, что отрицательный знак 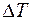 используется только при построении плана перемещений (стержень укорачивается от действия температуры), при решении системы уравнений величину
используется только при построении плана перемещений (стержень укорачивается от действия температуры), при решении системы уравнений величину 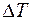 следует принять положительной.
следует принять положительной.
Примечание. Определение монтажных напряжений, связанных с неточностью изготовления одного из стержней 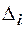 , производится так же, как температурных напряжений. Например, если в рассмотренном примере стержень 1 будет изготовлен короче, чем требуется, на величину
, производится так же, как температурных напряжений. Например, если в рассмотренном примере стержень 1 будет изготовлен короче, чем требуется, на величину 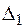 (эта величина в таблице исходных данных [4] задана отрицательной), то при сборке конструкции стержень 1 надо будет растянуть и при этом стержень 2 тоже растянется. На плане перемещений отрезок
(эта величина в таблице исходных данных [4] задана отрицательной), то при сборке конструкции стержень 1 надо будет растянуть и при этом стержень 2 тоже растянется. На плане перемещений отрезок 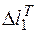 заменим на
заменим на 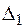 и решение задачи будет справедливо, если в полученной системе уравнений всюду заменить
и решение задачи будет справедливо, если в полученной системе уравнений всюду заменить 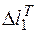 на заданную величину
на заданную величину 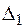 .(Отрицательный знак
.(Отрицательный знак 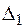 при решении системы уравнений не учитывается.)
при решении системы уравнений не учитывается.)
Дата добавления: 2016-01-09; просмотров: 1019;
