Движение тел в неинерциальных системах отсчета.
Пусть ускорение материальной точки равно 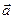 в инерциальной системе отсчета
в инерциальной системе отсчета 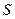 и равно
и равно 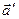 в неинерциальной системе
в неинерциальной системе  . Рассмотрим разность этих ускорений
. Рассмотрим разность этих ускорений
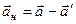 .
.
Для поступательного движения системы  величина
величина 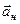 равна ускорению системы
равна ускорению системы  относительно
относительно 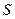 .
.
В инерциальной системе 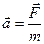 , где
, где 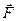 - сила, действующая на материальную точку со стороны некоторого тела. Тогда ускорение
- сила, действующая на материальную точку со стороны некоторого тела. Тогда ускорение 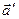 можно представить в виде
можно представить в виде
 .
.
Умножая это уравнение на массу 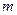 , получим
, получим
 .
.
Для того, чтобы сохранить вид 2-го закона Ньютона в неинерциальной системе отсчета, удобно ввести силу инерции
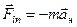 .
.
Тогда 2-ой закон Ньютона в неинерциальной системе можно представить в виде
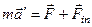 .
.
Сила инерции не является силой по определению, данному в лекции 3. Это некоторое формальное понятие, удобное для описания движения в неинерциальных системах. Однако, как будет видно из дальнейшего рассмотрения, ее проявления являются совершенно реальными.

В случае вращательного движения системы  так просто ввести силу инерции уже не удается, так как в этом случае разные точки
так просто ввести силу инерции уже не удается, так как в этом случае разные точки  движутся с разным ускорением. Рассмотрим силы инерции во вращающейся системе на простом примере. Будем считать, что система
движутся с разным ускорением. Рассмотрим силы инерции во вращающейся системе на простом примере. Будем считать, что система  представляет собой равномерно вращающийся с угловой скоростью
представляет собой равномерно вращающийся с угловой скоростью  плоский диск радиуса
плоский диск радиуса  (рис. 1). Пусть материальная точка массы
(рис. 1). Пусть материальная точка массы 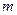 движется по краю диска со скоростью
движется по краю диска со скоростью 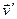 относительно диска. Скорость точки относительно
относительно диска. Скорость точки относительно 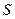 равна
равна
 .
.
Ускорение относительно инерциальной системы
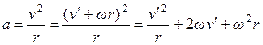 .
.
В неинерциальной системе 
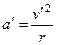 ,
, 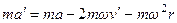 .
.
Как следует из опыта, реальная сила, действующая на материальную точку со стороны других тел, не зависит от системы отсчета, то есть  . Тогда последнее уравнение можно переписать в виде
. Тогда последнее уравнение можно переписать в виде
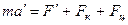 .
.
Здесь 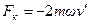 - сила Кориолиса,
- сила Кориолиса, 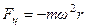 - центробежная сила. Знак минус означает, что в данном случае обе силы направлены в сторону от центра диска. Как видно из этих выражений, во вращающейся системе сила Кориолиса возникает только в случае дви-жения материальной точки в этой системе (
- центробежная сила. Знак минус означает, что в данном случае обе силы направлены в сторону от центра диска. Как видно из этих выражений, во вращающейся системе сила Кориолиса возникает только в случае дви-жения материальной точки в этой системе ( 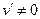 ).
).

Можно показать, что в общем случае вектор силы Кориолиса выражается через вектора 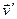 и
и  следующим образом
следующим образом
 .
.
Земля представляет собой естественную вращаю-щуюся систему отсчета с периодом вращения 24 часа. Поэтому на тела, движущиеся относительно Земли, действует сила Кориолиса. На рис. 2 показаны направления ее действия для различных случаев движения. Ее действие проявляется, например, в том, что у рек в северном полушарии всегда подмывается правый берег, а у рек в южном полушарии – левый.
ЛЕКЦИЯ 23
Дата добавления: 2016-01-09; просмотров: 767;
