ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ДИНАМИЧЕСКОГО СИНТЕЗА

Задачи ТММ могут быть разделены на две основные группы: задачи анализа и задачи синтеза механизмов и машин.

Анализом называется исследование и определение структурных, кинематических и динамических свойств механизмов и машин по их заданной схеме.

Синтезом называется проектирование схемы механизма или машины по их заданным структурным, кинематическим и динамическим свойствам, то есть задачи синтеза являются обратными задачами анализа.

В настоящей работе рассматриваются задачи синтеза плоских рычажных механизмов с одной степенью свободы (в части подбора масс звеньев, обеспечивающих заданную неравномерность движения механизма).

Неравномерность движения механизма определяют по изменению обобщенной скорости его начального звена, с которым связана обобщенная координата. Движение остальных звеньев определяется на основании кинематического анализа механизма.

Движение механизма в общем случае характеризуется тремя режимами: разбега (разгона), установившегося движения и выбега (торможения). Разбег и выбег относятся к режимам неустановившегося движения. Процессы, происходящие в машине при работе в этих режимах, называются переходными.

При разбеге скорость начального звена возрастает, при выбеге – убывает. Возрастание скорости происходит до наступления режима установившегося движения, снижение скорости – после его завершения или, для некоторых механизмов, сразу после разгона. При работе механизма в установившемся режиме его кинетическая энергия и, соответственно, скорость начального звена колеблются около некоторого среднего значения и периодически повторяются, то есть являются периодическими функциями времени. Минимальный промежуток времени, через который повторяются значения кинетической энергии и обобщенной скорости, называется циклом установившегося движения. Для многих машин цикл установившегося движения соответствует одному обороту вращающегося звена механизма, принимаемого за начальное звено. Однако для некоторых машин, например для двигателей внутреннего сгорания, цикл установившегося движения может соответствовать двум и более оборотам кривошипа кривошипно-ползунного механизма двигателя. В частном случае при установившемся движении скорость начального звена может быть постоянной.

В общем случае машина за период работы от пуска до остановки может работать в нескольких установившихся режимах и соответственно нескольких режимах разгона и торможения.

На рис. 1 в качестве примера показан график изменения угловой скорости w начального звена механизма, работающего в течение времени Т в двух режимах установившегося движения.

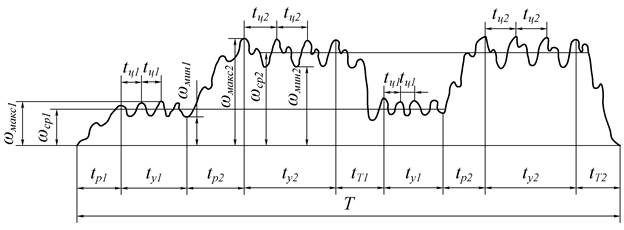
Рисунок 1 – График изменения угловой скорости начального звена механизма при работе в двух режимах установившегося движения

Разбег машины с момента пуска (t = 0) происходит в течение времени t_р1 до начала ее работы в первом режиме установившегося движения, который продолжается в течение времени t_у1 с циклом t_ц1. При переходе на второй режим установившегося движения скорость начального звена снова возрастает в течение времени разгона t_р2 до начала нового, второго режима установившегося движения, которое продолжается в течение времени t_у2 с циклом t_ц2. После завершения работы в этом скоростном режиме установившегося движения скорость начального звена снижается в течение времени t_Т1 до наступления очередного периода работы механизма в первом и далее втором режимах, после чего машина останавливается с выбегом в течение времени t_Т2. На рис.1 4-м циклам установившегося движения соответствуют 5 циклов неустановившегося движения: 3 разгона и 2 торможения.

При динамическом синтезе механизмов в общем случае могут решаться различные задачи, которые зависят от условий синтеза. К этим условиям могут относиться требования учета жесткости звеньев механизма и законов нагружения механизма в периоды разгона и торможения. При выполнении данного раздела курсового проекта в учебных целях звенья принимаются абсолютно жесткими, а законы движения механизма в периоды разгона и торможения не рассматриваются. В этом случае основным условием синтеза становится определение такого момента инерции маховика (дополнительной массы), при котором под действием заданных сил обеспечивается закон движения начального звена при установившемся режиме, удовлетворяющем заданному коэффициенту неравномерности движения d.

Коэффициент неравномерности при вращательном движении начального звена определяется из выражения

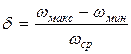, (1)

где w_макс, w_мин – соответственно максимальная и минимальная угловые скорости начального звена за цикл установившегося движения;

w_ср – средняя угловая скорость начального звена за цикл установившегося движения.

На рис. 1 обозначения максимальной, минимальной и средней угловых скоростей при различных режимах установившегося движения приведены с индексами 1 и 2.

Скорость w_ср определяется из выражения

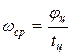, (2)

где j_ц – угол поворота начального звена за цикл установившегося движения;

t_ц – время цикла установившегося движения.

Время цикла находят интегрированием из соотношения

,

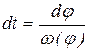где w(j) – аналог угловой скорости начального звена.

После интегрирования на угле j_ц имеем

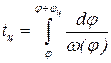, (3)

где w(j) – текущая угловая скорость начального звена в зависимости от его углового положения в цикле установившегося движения.

Подставляя найденное выражение для 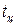в формулу (2) получим

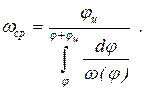(4)

Функция w(j) определяется из решения дифференциального уравнения движения начального звена.

В рассматриваемой задаче динамического синтеза силы, действующие на звенья механизма, зависят от положений звеньев механизма. В этом случае для описания движения механизма удобнее использовать уравнение движения в форме уравнения кинетической энергии

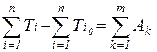, (5)

где 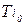, 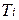– кинетическая энергия i-го звена механизма в начале и конце рассматриваемого промежутка времени;

А_k – работа каждой k-ой из m внешних и внутренних сил и пар сил (моментов), приложенных к звеньям механизма;

n – число подвижных звеньев механизма.

При решении уравнения (5) необходимо выполнить большой объем вычислений, связанный с многократным суммированием кинетических энергий всех подвижных звеньев механизма и работ всех приложенных к ним сил. Для упрощения решения это уравнение заменяется тождественным ему уравнением движения условного механизма, содержащего всего одно подвижное звено с таким же законом движения, как у начального звена реального механизма. Замену уравнения (5) ему тождественным выполняют путем приведения сил и масс к начальному звену. Это звено фактически становится подвижным звеном условного механизма и называется звеном приведения.

Условный механизм, состоящий из одного подвижного звена, связанного со стойкой, обладающего приведенным моментом инерции (или приведенной массой), нагруженного приведенным моментом сил (или приведенной силой) и с таким же законом движения как у начального звена называется динамической моделью реального механизма. На основании решения уравнения движения звена приведения определяют закон движения начального звена и по нему – законы движения остальных звеньев механизма.

В общем случае в состав механизма могут входить звенья, совершающие вращательное, поступательное или сложное (плоскопараллельное) движение.

Кинетическая энергия этих звеньев определяется из выражений:

для звеньев, совершающих вращательное движение

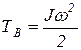; (6)

для звеньев, совершающих поступательное движение

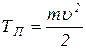; (7)

для звеньев, совершающих сложное (плоскопараллельное) движение

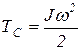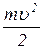+ , (8)

где J – момент инерции вращающегося звена относительно оси вращения, или звена, совершающего сложное (плоскопараллельное) движение относительно оси, проходящей через центр масс звена перпендикулярно плоскости движения;

w – угловая скорость звена;

m – масса звена;

u – поступательная скорость центра масс звена.

Для решения уравнения движения звена приведения в зависимости от вида его движения (поступательное или вращательное) необходимо в случае его поступательного движения определить приведенную массу и приведенную силу, либо, в случае его вращательного движения, приведенный момент инерции звена и приведенный момент сил.

Методика определения этих характеристик идентична для обоих видов движения и основана на использовании уравнения кинетической энергии (5). Для звена приведения, совершающего вращательное движение, это уравнение принимает вид

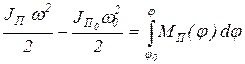, (9)

где 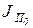, J_П – приведенные моменты инерции звена приведения относительно оси его вращения в начале и конце рассматриваемого промежутка времени, в течение которого обобщенная координата изменяется от j₀ до j, а угловая скорость – от w₀ до w;

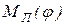– приведенный момент сил;

Для поступательно движущегося звена приведения имеем

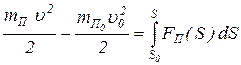, (10)

где 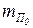, 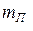– приведенные массы звена в начале и конце рассматриваемого промежутка времени, в течение которого обобщенная координата изменяется от S₀ до S, а скорость от u₀ до u;

F_П(S) – приведенная сила.

Для того чтобы звено приведения двигалось также как начальное звено реального механизма необходимо, чтобы в зависимости от вида движения звена приведения либо уравнение (9) либо уравнение (10) было тождественным уравнению (5), то есть выполнялось бы равенство их левых и правых частей. Для вращающегося звена приведения указанное равенство левых частей имеет вид:

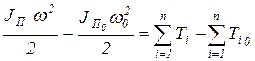; (11)

равенство правых частей

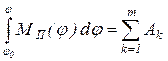. (12)

Из уравнения (11) получаем выражение для определения приведенного момента инерции вращающегося звена приведения

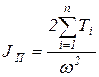. (13)

Для поступательно движущегося звена приведения аналогичным образом определяем выражение для приведенной массы

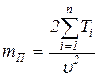. (14)

Отсюда следуют определения:

Приведенным моментом инерции называется условный момент инерции вращающегося звена приведения относительно оси его вращения, кинетическая энергия которого равна сумме кинетических энергий всех подвижных звеньев механизма.

Приведенной массой называется масса поступательно движущегося звена приведения, кинетическая энергия которого равна сумме кинетических энергий всех подвижных звеньев механизма.

При сложном плоскопараллельном движении кинетическая энергия i – того звена определяется по формуле

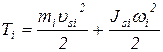, (15)

где: m_i – масса i – того звена;

u_si – скорость центра масс i – того звена;

w_i – угловая скорость i – того звена;

J_si – момент инерции i – того звена относительно оси, проходящей через его центр масс перпендикулярно плоскости движения.

Подставляя выражение (15) в (13) и (14), после преобразований получим

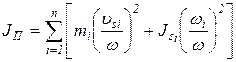; (16)

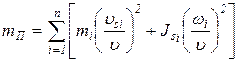. (17)

Приведенный момент или приведенная сила сил определяется из условия равенства элементарной работы (или мощности), совершаемой на рассматриваемом возможном перемещении звена приведения, сумме элементарных работ (мощностей) действительных сил и моментов сил, приложенных к звеньям механизма. Это условие выражается равенством правой части уравнения (5) правым частям уравнений (9) и (10).

Отсюда следуют определения:

Приведенной силой называется условная сила, приложенная в заданном направлении к выбранной точке на звене приведения и определяемая из равенства мощности (элементарной работы) этой силы сумме мощностей (элементарных работ) сил и пар сил (моментов), действующих на звенья механизма.

Точка, к которой прикладывается приведенная сила, называется точкой приведения.

Приведенным моментом сил называется условный момент пары сил, приложенный к звену приведения и определяемый из условия равенства мощности (элементарной работы) этого момента сумме мощностей (элементарных работ) сил и пар сил (моментов), приложенных к звеньям механизма.

В общем случае мощность N силы 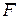определяется из соотношения

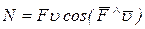, (18)

где u – скорость точки приложения силы;

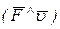– угол между векторами силы и скорости точки ее приложения (угол давления).

Мощность характеризуется знаком. Отрицательные значения мощности соответствуют противоположным направлениям вектора скорости и векторной проекции вектора силы на линию действия вектора скорости.

Приведенную силу на вращающемся звене приведения обычно прикладывают в характерной точке звена (например, совпадающей с центром вращательной кинематической пары, соединяющей звено приведения с другим подвижным звеном) в направлении перпендикулярном радиус-вектору этой точки относительно оси вращения. В этом случае векторы силы и скорости точки ее приложения расположены на одной линии, угол 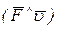= 0 либо 180 и мощность приведенной силы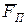

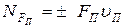, (19)

где: u_П – скорость точки приведения.

Мощность 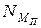приведенного момента сил М_П

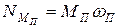, (20)

где: w_П – угловая скорость звена приведения.

Выражения для определения суммарных мощностей приведенной силы 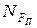и приведенного момента сил 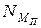аналогичны:

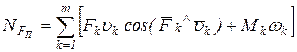, (21)

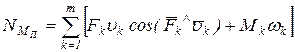, (22)

где F_k, M_k – действительные силы и моменты сил, действующие на звенья механизма;

u_k – скорости точек приложения сил F_k;

w_k – угловые скорости звеньев, на которые действуют пары сил с моментами M_k;

m – число подвижных звеньев механизма.

Из этих формул с учетом (19) и (20) получим выражения для определения приведенной силы F_П и приведенного момента M_П:

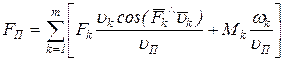; (23)

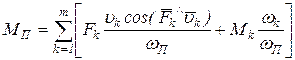. (24)

Приведенная сила и приведенный момент сил являются скалярными величинами и могут быть как положительными, так и отрицательными. При положительном их значении направления приведенной силы и приведенного момента совпадают с направлением скорости (линейной или угловой) звена приведения, при отрицательном они направлены противоположно.

В зависимости от поставленной задачи приводят либо все силы, приложенные к звеньям механизма, либо отдельные силы: силы движущие, силы сопротивления, силы тяжести, силы трения и другие.

Выполнив приведение масс и моментов инерции звеньев механизма, сил и моментов сил, действующих на звенья, переходят к решению дифференциального уравнения движения начального звена (звена приведения) по формулам (9) или (10). Для этого необходимо выполнить по отдельности приведение сил движущих и сил сопротивления. Затем в правую часть уравнения (9) в качестве приведенного момента М_П (φ) записать разницу приведенных моментов сил движущих и сил сопротивления или соответственно для уравнения (10) в качестве приведенной силы F_П (S) записать разницу приведенных сил движущих и сил сопротивления. Для звена приведения, совершающего вращательное движение, приведенный момент сил

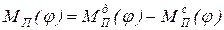, (25)

где 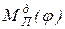, 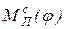– приведенные моменты сил движущих и сил сопротивления в функции угла поворота φ звена приведения.

Для поступательно движущегося звена приведенная сила

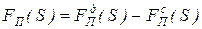, (26)

где 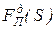, 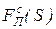– приведенные движущие силы и силы сопротивления.

Из уравнения (9) получаем выражение для определения угловой скорости звена приведения

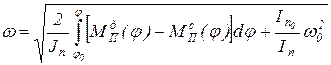_. (27)

Интегрируя выражение в квадратных скобках под корнем при заданных начальных условиях t = t₀; φ = φ₀; ω = ω_0, получают решение дифференциального уравнения движения, из которого определяют угловую скорость 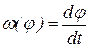, время поворота 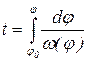и угол поворота 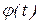звена приведения.

Аналогично из уравнения (10) получают выражение для определения скорости поступательно движущегося звена приведения

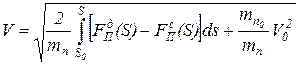_. (28)

Для решения дифференциального уравнения (27) движения звена приведения в режиме установившегося движения необходимо знать начальные условия t₀, φ₀ и ω₀, соответствующие началу работы механизма в этом режиме.

Точное начало режима установившегося движения определяется на основании исследования работы механизма в переходном режиме или с момента пуска машины или с момента с момента перехода на новый режим работы.

При исследовании работы условного механизма с вращающимся звеном приведения в переходном режиме в момент пуска его начальная угловая скорость 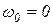и формула (27) принимает вид:

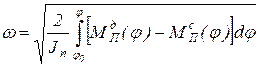. (29)

В зависимости от типа исследуемой машины одна из функций 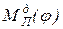либо 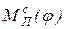считается заданной, а другая принимается за константу и определяется из условия равенства работ сил движущих и сил сопротивления. Начало режима установившегося движения соответствует первому значению угловой скорости ω₀ звена приведения, которое затем периодически повторяется через промежутки времени, равные циклу установившегося движения. Это первое значение ω₀ и соответствующие ему значения t₀ и φ₀ являются начальными условиями для решения дифференциального уравнения движения звена приведения в режиме установившегося движения.

При работе в установившемся режиме в течение каждого цикла происходят изменения движущих сил, сил сопротивления и кинетической энергии звеньев механизма. Эти величины являются периодическими функциями угла поворота φ звена приведения, а период функции 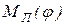(25) равен или кратен периоду функции 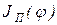. Значения линейной или угловой скорости звена приведения, полученные из выражений (28) или (29) для цикла установившегося движения, будут переменными, а скорость звена приведения будет представлять собой периодическую функцию времени.

Переменная скорость звена приведения обуславливает неравномерность движения механизма. Различают два вида неравномерности: периодическую и непериодическую. Непериодическая неравномерность возникает при переходных режимах работы машины, периодическая – при установившемся движении. Задача динамического синтеза рычажных механизмов по заданному коэффициенту неравномерности движения при выполнении курсового проекта решается, исходя из условия их работы с периодической неравномерностью в режиме установившегося движения.

Количественно периодическая неравномерность оценивается коэффициентом неравномерности движения δ, определяемым по формуле (1). Увеличение коэффициента δ соответствует увеличению амплитуды колебаний, скорости звеньев механизма, их ускорений и сил инерции, действующих на звенья и опорные конструкции машины. Возникающие при этом вибрации могут привести к быстрому выходу ее из строя, разрушению фундаментов и снижению качества выполнения технологических операций. Поэтому при синтезе механизмов в зависимости от их назначения задаются допустимыми значениями коэффициента d. Эти значения представляет собой небольшую величину, которая находится в большинстве случаев в пределах 0,001 – 0,2. Например, для металлорежущих станков она принимается 0,002 – 0,04, для прокатных станов 0,25 – 0,45, для двигателей внутреннего сгорания 0,05 – 0,07.

Ввиду малости коэффициента δ среднюю угловую скорость ω_ср начального звена в выражении (1) при динамическом синтезе принимают равной ее среднему арифметическому значению из максимального и минимального значений за цикл установившегося движения:

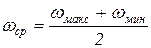. (30)

Подставляя это значение в формулу (1), получим значения максимальной и минимальной скорости в цикле установившегося движения

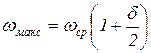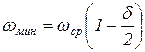; . (31)

На практике отличие ω_макс и ω_мин от ω_ср составляет не более ±2%. Чем меньше это отличие, тем лучше динамические характеристики и выше качество машины. Поэтому при проектировании механизмов стремятся минимизировать значение коэффициента неравномерности движения δ. В курсовом проектировании это достигается установкой на приводном валу машины, связанным с входным звеном, дополнительной массы, которая называется маховиком. При динамическом синтезе механизмов начальное звено (звено приведения) обычно совмещают с входным. На практике маховик выполняется в виде колеса с равномерно распределенной массой по окружности. Маховик увеличивает инертность механизма, уменьшает диапазон изменения угловой скорости приводного вала и соответственно уменьшает коэффициент δ.

В некоторых случаях маховик может быть установлен на одном из валов привода механизма, угловая скорость которого отличается от угловой скорости вала приведения. Место установки определяется конструкцией и назначением машинного агрегата.

В общем случае маховик рекомендуется устанавливать ближе к источнику возбуждения неравномерности движения. Например, в машинах с двигателем внутреннего сгорания, в которых источником возбуждения неравномерности движения является коленчатый вал двигателя, маховик целесообразно устанавливать на коленчатом валу двигателя. В машинах с электроприводом, например в прокатных станах, в которых передача движения от двигателя к прокатным валкам осуществляется через редуктор, маховик лучше устанавливать после редуктора на валу, соединяющем редуктор с валками, которые являются источником неравномерности движения.

При установке маховика не на валу приведения масс выполняется перерасчет момента инерции маховика, исходя из условия равенства кинетических энергий маховика при условии его установки на валу приведения масс и на валу его действительной установки.

Задачей динамического синтеза механизма по заданному коэффициенту неравномерности движения δ является определение момента инерции маховика, ограничивающего колебания угловой скорости приводного вала машины в заданных этим коэффициентом пределах.

При определении момента инерции маховика заданным, кроме коэффициента δ, является также среднее значение угловой скорости ω_ср звена приведения. Среднюю угловую скорость задают в зависимости от технологических требований и номинальной частоты вращения вала двигателя, указанной в его паспорте, с учетом передаточного отношения между валом двигателя и звеном приведения. Угловую скорость ω_д вала двигателя при известной частоте его вращения 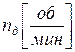определяют из соотношения

.

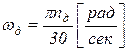Подвижные звенья механизма можно разделить на две группы. При установке маховика и звена приведения на одном валу к первой группе вместе с маховиком и начальным звеном относят звенья, связанные с начальным звеном постоянным передаточным отношением. К этой группе относятся зубчатые колеса, муфты и т.п. Приведенный момент инерции звеньев первой группы является постоянным, так как при постоянном передаточном отношении приведенный момент инерции не зависит от положения звеньев.

Ко второй группе относятся звенья, передаточные отношения которых изменяются в течение цикла установившегося движения. К ним относятся шатуны, ползуны и другие звенья, характеризуемые переменным отношением их скоростей к скорости звена приведения. При этом важно подчеркнуть, что экстремальные значения переменного приведенного момента инерции звеньев второй группы совпадают с экстремальными значениями приведенного момента инерции 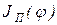всего механизма, выражение для которого можно записать в виде

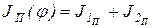(j), (32)

где 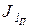и 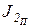(j) - приведенные моменты инерции первой и второй групп звеньев механизма.

Угловая скорость w звена приведения изменяется внутри цикла t_ц установившегося движения от w_мин до w_макс (рис. 2), которым соответствуют углы поворота звена j₁ и j₂. Для времени движения между этими углами уравнение движения механизма в форме уравнения кинетической энергии (9) будет иметь вид

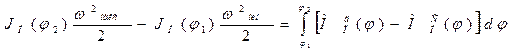, (33)

где 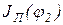, 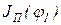- приведенные моменты инерции звена приведения при углах поворота j₂ и j₁.

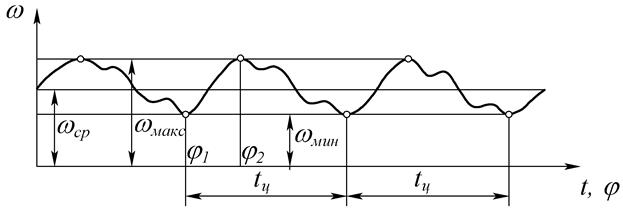
Рисунок 2 – Изменение угловой скорости звена приведения

при установившемся движение

Приведенный момент инерции первой группы звеньев 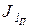является постоянным и его можно представить в виде

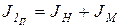, (34)

где J_Н – постоянная часть приведенного момента инерции механизма;

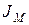– момент инерции маховика.

Постоянная часть J_Н приведенного момента инерции легко определяется по заданным массовым характеристикам звеньев механизма.

Подставляя выражение (34) в (32) и далее в (33), после преобразований получим

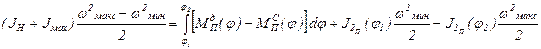. (35)

В формуле (35) выражение 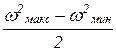с учетом (31) можно представить в виде

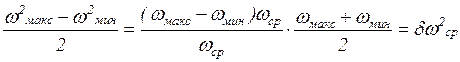. (36)

После подстановки полученного выражения в (35) и несложных дополнительных преобразований получим выражение для определения момента инерции маховика

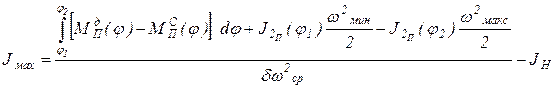. (37)

Из этого выражения следует, что для уменьшения неравномерности движения механизма, т.е. коэффициента d, необходимо увеличивать момент инерции (массу) маховика. Однако добиться полной равномерности движения, т.е. значения d = 0, путем увеличения момента инерции маховика невозможно, так как в этом случае момент инерции J_мах должен быть равен бесконечности.

Из уравнения (37) следует, что для определения момента инерции маховика аналитическим методом необходимо знать функци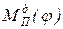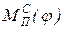и , и 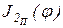в явном виде и по ним определить значения j₁, j₂, 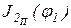и 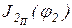в пределах цикла установившегося движения.

Для каждой машины указанные функции различны и могут быть получены только в приближенном виде. Аналитические выражения для этих функций получить достаточно сложно, а возможные при этом неточности могут привести к серьезным ошибкам в расчете маховика. Поэтому на практике для расчета маховика используются графоаналитические методы, при которых эти функции задаются или строятся в виде графиков с последующей их обработкой. Обработка этих графиков по существу представляет собой графическое решение дифференциального уравнения установившегося движения начального звена механизма в форме уравнения (9) кинетической энергии, в результате которого определяются закон движения начального звена w(j) – функция (27), значения w _макс и w _мин и по ним – момент инерции маховика.

Существует два наиболее применяемых графоаналитических метода определения момента инерции маховика: метод Мерцалова и метод с применением графика энергомасс, предложенный немецким ученым Виттенбауэром. Метод Мерцалова основан на графоаналитическом решении уравнения (37). Более точным считается метод Виттербауэра, на основе которого построено дальнейшее изложение вопроса о динамическом синтезе рычажного механизма по заданному коэффициенту неравномерности его движения.