Диссипативная функция.

К числу диссипативных сил относятся силы сопротивления дви­жению точек системы, направленные противоположно их скоростям. Мы рассмотрим случай сил сопротивления, представимых в виде

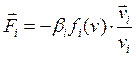, (4.28)

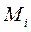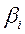где — величина скорости точки ; и 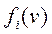— положительные функции от обобщенных координат и соответственно от скоростей 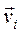. По (4.10) и (4.20) (первое тождество Лагранжа) соответствующие этим силам обобщенные силы определяются равенствами

, .

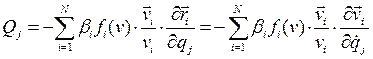Заметив, что

,

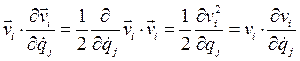находим

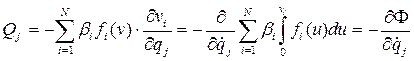(4.29)

где через Ф обозначена величина, называемая диссипативной функцией

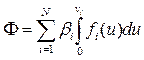(4.30)

Заметим, что Ф>0, так как подынтегральные функции положи­тельны. Диссипативная функция была введена в классическом труде Релея «Теория звука» для сил сопротивления, пропорциональных первой степени скорости. Здесь это понятие обобщено на силы более общего вида. В случае одночленной степенной зависимости сил сопротивления от скорости 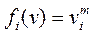диссипативная функция

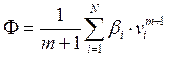(4.31)

будет однородной функцией (m+1) степени от обобщенных скоро­стей, которую легко выразить через мощность диссипативных сил

(4.32)

Здесь применена теорема Эйлера об однородных функциях. Отметим, что m = 0 соот­ветствует кулонову (сухому) трению, m=1—силам вязкого трения, пропорциональным первой степени скорости (случай Релея), m = 2 — силам квадратичного сопротивления.

При составлении обобщенных сил по формуле (4.29) необходимо иметь в виду, что дифференцируются выражения, содержащие модуль обобщенных скоростей. Например, при сопротивлении, пропорцио­нальном четной степени скорости и n =1 (одна степень свободы)

(4.33)

где 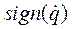означает знак функции φ ( )= 1, если φ > 0 и =-1, если φ < 0).