Уравнения динамики системы материальных точек и твёрдого тела.
Предварительные замечания об общих теоремах динамики. Задача об интегрировании дифференциальных уравнений движения материальной точки, представляющая даже в случае одной точки некоторые трудности, становится подчас непосильной, когда приходится иметь дело с движением системы материальных точек. Силы, приложенные к отдельным точкам системы, могут зависеть от положения и движения остальных точек системы, так что правые части дифференциальных уравнений, написанных для каждой точки в отдельности, будут содержать время, координаты и проекции скорости всех точексистемы. В результате вопрос сводится к интегрированию системыдифференциальных уравнений. Но иногда оказывается достаточным определить изменение некоторых суммарных мер движения системы в целом (количества движения, момента количества движения, кинетической энергии) в зависимости от суммарных мер действия сил (главный вектор и главный момент приложенных сил, работа сил, потенциальная энергия). Такого рода соотношения между изменениями во времени суммарных мер движения системы материальных точек и суммарными мерами действия приложенных к точкам совокупности сил выражают общие теоремы динамики системы материальных точек, применяемые как для отдельных точек и их систем, так и для сплошных сред. К числу общих теорем динамики относятся: теорема об изменении количества движения с ее модификациями - теоремой импульсов и теоремой о движении центра масс, теорема об изменении момента количеств движения (кинетического момента), а также теорема об изменении кинетической энергии.
 В основе вывода первых двух общих теорем динамики- количества движения и момента количества движения - лежит идея выделения из всех сил, приложенных к системе, внутреннихсил взаимодействия между материальными точками системы. Внутренние силы в своей совокупности не могут влиять на такие суммарные меры движения, как главный вектор и главный момент количеств движения точек системы. Только внешние силы, действующие на точки системы со стороны внешних тел, не принадлежащих к рассматриваемой системе, могут изменять главный вектор и главный момент количеств движения системы. В использовании этого свойства внутренних сил, представляющего собой одно из важнейших следствий третьего закона Ньютона, заключается главное значение двух первых общих теорем динамики. Рассмотрим систему, состоящую из n точек. На каждую из них действуют силы со стороны других точек (рис. 52), причём
В основе вывода первых двух общих теорем динамики- количества движения и момента количества движения - лежит идея выделения из всех сил, приложенных к системе, внутреннихсил взаимодействия между материальными точками системы. Внутренние силы в своей совокупности не могут влиять на такие суммарные меры движения, как главный вектор и главный момент количеств движения точек системы. Только внешние силы, действующие на точки системы со стороны внешних тел, не принадлежащих к рассматриваемой системе, могут изменять главный вектор и главный момент количеств движения системы. В использовании этого свойства внутренних сил, представляющего собой одно из важнейших следствий третьего закона Ньютона, заключается главное значение двух первых общих теорем динамики. Рассмотрим систему, состоящую из n точек. На каждую из них действуют силы со стороны других точек (рис. 52), причём 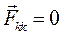 и
и  . На каждую точку системы действует равнодействующая
. На каждую точку системы действует равнодействующая  , но сумма всех равно действующих
, но сумма всех равно действующих  , где
, где 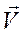 - главный вектор всех внутренних сил. Нетрудно увидеть, что и сумма моментов всех внутренних сил, независимо от выбора центра, также будет равен нулю. Итак, главный вектор и главный момент всех внутренних сил, действующих на систему точек, равны нулю.
- главный вектор всех внутренних сил. Нетрудно увидеть, что и сумма моментов всех внутренних сил, независимо от выбора центра, также будет равен нулю. Итак, главный вектор и главный момент всех внутренних сил, действующих на систему точек, равны нулю.
Теорема об изменении кинетической энергии устанавливает связь между изменением основной меры движения системы материальных точек- кинетической энергии и мерой действия сил на протяжении путей движения точек системы - работой сил. Таким образом, в круг вопросов механики вводится понятие энергии. Значение этого понятия состоит в том, что им определяется единая физическая величина, проявляющаяся в различных физических явлениях и, таким образом, связывающая их между собой. Понятие энергии объединяет механику с термодинамикой, с учением об электрических явлениях и т. п. Преобразование механической энергии в другие формы энергии и обратное преобразование этих форм в механическую энергию представляет важную задачу современной техники.
В отличие от изменения количества движения и момента количества движения изменение кинетической энергии материальной системы зависит от работы как внешних, так и внутренних сил. Однако и в этом случае выделение класса внутренних сил оказывается полезным, так как, например, в случае движения абсолютно твердого тела или системы абсолютно твердых тел работа внутренних сил равна нулю, а в случае сплошной среды она позволяет судить о потерях механической энергии за счет внутреннего трения.
Дата добавления: 2016-01-07; просмотров: 866;
