Основные положения и аксиомы динамики

При описании процессов, происходящих в окружающем нас мире, мы используем определенные математические модели; эти модели правильно отражают основные, главные свойства материи и по мере увеличения наших знаний все более усложняются, что дает возможность описывать процессы, характер протекания которых на предыдущем этапе исследований был нам еще не ясен.

Классическая механика- механика Ньютона - является одной из таких моделей; она изучает законы, которым под­чиняются процессы движения материальных тел в простран­стве. При этом пространство наделяется рядом свойств: оно считается трехмерным, евклидовым и непрерывным.

Трехмерность пространства означает, что положение любого его места (точки) определяется тремя величинами — тремя координатами; обычно употребляются три декартовы (прямоугольные) координаты; при этом принимается посту­лат о возможности отсчитывать эти координаты от некото­рой неподвижной точки (начала координатной системы).

Пространство считается евклидовым, что предполагает отсутствие в нем кривизны; иначе говоря, принимается посту­лат Евклида о том, что параллельные прямые не пересека­ются. С физической точки зрения это положение соответ­ствует утверждению, что свойства пространства не зависят от содержащегося в нем вещества. Наконец, пространство предполагается непрерывным, т.е. считается, что расстояние между двумя точками может быть сколь угодно малым и не существует предельно малой длины, которая бы ограничивала малость расстояний и размеров.

Движение материальных тел в пространстве осуществля­ется с течением времени. В механике Ньютона время не свя­зано с пространством и темп течения времени принимается одинаковым для всех тел, независимо от скоростей их дви­жения; время также считается непрерывным. Всё это представляется нам совершенно естественным, как необходимые поправки оказываются несущественны для тех относительно небольших, по сравнению со скоростью света, скоростей и больших, в сравнении с элементарными частицами, размеров движущихся тел, с которыми мы встречаемся при изучении обычных процессов движения. Однако все это не совсем верно; это лишь первое приближение к познанию явлений, происходящих в окружающем насмире. Мы теперь знаем, что механика Ньютона неприменима к изучению процессов движения, происходящих с большими скоростями, и при рассмотрении явлений, про­исходящих в микромире. Данные современной науки позво­ляют утверждать, что пространство имеет кривизну, которая зависитот распределения в нем тяготеющих масс; что время нельзяотрывать от пространства: трехмерное пространство и времяследует заменить четырехмерным пространственно-временным континуумом; темп времени и размеры движу­щихся тел зависят от скорости движения наблюдателя. На­конец, изменилось и понятие массы как неизменной характе­ристики инерции каждого отдельного тела; оказалось, что масса является переменной величиной и зависит от скоростидвижения тела. В последнее время возникли серьезные сомнения в непре­рывности пространства и времени; по-видимому, простран­ство и время, так же как и вещество, надо считать дискрет­ными, т. е. существуют наименьшие размеры и наименьший интервал времени — кванты пространства и времени.

Таким образом, классическая механика не может описы­вать движение тел при любых условиях и имеет ограниченную область применения — при немалых размерах движущихся тел и при небольших скоростях их движения. В этом диапазоне механика Ньютона оправдала себя многочислен­ными совпадениями процессов движения тел, предсказанных расчетами, с действительно происходящими и наблюдаемыми в природе и в технике.

Классическая механика опирается на ряд положений, аксиом, провозглашаемых без доказательства, а затем, на базе принятых положений, выводятся дифференциальные уравнения движения материальной точки и системы матери­альных точек, уравнения движения твердого тела, общие тео­ремы и вариационные принципы, позволяющие решать конкретные частные задачи. В ряде случаев это оказывается недостаточным. Тогда приходится обращаться к экспериментам и вытекающим из них законам, устанавливающим зависимости действующих на тела сил от их взаимного расположения, от скоростей ихдвижения и т. п. Так, в теоретической механике используют­ся; закон всемирного тяготения Ньютона, закон Гука (для упругих сил), законы Кулона (для сил трения), аэродинами­ческие законы сопротивления движению твердых тел в жид­кой и газообразной средах и др.

В теоретической механике с успехом применяются абстрактные понятия материальной точки и абсолютно твер­дого тела. Под материальной точкой понимается модель тела, размерами которого в данной задаче можно пренебречь, но оно обладает конечной массой. На определенном этапе изучения ме­ханики становится очевидным, что материальной точкой мо­жно называть тело любого размера, если не учитывается его вращение.

Абсолютно твердым телом называется такое тело, расстояние между двумя любыми точками которого не изменяется. Иначе говоря, твердое тело предполагается настолько жестким, что можно пренебречь его деформациями. Окружающие нас материальные тела находятся в непрерывном движении и взаимодействуют друг с другом. Поскольку понятие «движение» можно трактовать весьма широко, следует оговорить, что здесь под движением понимается перемещение тел в пространстве с течением времени. Взаимодействия тел, результатом которых является их движение, будем называть силами. Пространство и время являются формами существования материи, и как материальное тело не может существовать вне пространства (и времени), так не бывает и «пустого пространства», т. е. пространства без материальных тел. Даже в глубоком космосе имеется вещество, достаточное количество частиц, хотя бы и в очень малой концентрации. Тем не менее можно представить себе материальную точку, помещенную в «пустое пространство», иначе говоря, настолько удаленную от остальных материальных тел, что их действиями на нее можно пренебречь; такая материальная точка называется изолированной.

Аксиома 1 (первый закон Ньютона): ускорение изолированной материальной точки равно нулю:

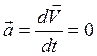
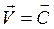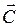Интегрируя это уравнение, получаем , где --постоянный вектор, который может быть и нулём. Т.о., первую аксиому можно сформулировать так: изолированная материальная точка неподвижна или движется с постоянной по величине и направлению скоростью.

Если же материальная точка не изолирована, то на нее действуют другие материальные тела, вследствие чего у рас­сматриваемой материальной точки появляется ускорение; ко­личественное выражение этого ускорения определяется вто­рой аксиомой динамики.

Аксиома 2 (второй закон Ньютона): ускорение, приоб­ретаемое материальной точкой при действии на нее силы, пропорционально величине этой силы и направлено по на­правлению действия силы. Вторая аксиома выражается век­торной формулой

,

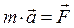в которой коэффициент пропорциональности т, называемый массой точки, определяет меру сопротивляемости точки из­менению ее движения, т. е. характеризует инерцию точки. Из второго закона Ньютона непосредственно следуют диф­ференциальные уравнения движения материальной точки. Сила, которая приложена к данной точке (телу) и сооб­щает ей ускорение, есть результат действия на нее некоторого другого тела. Очевидно, что и это другое тело испытывает действие силы со стороны данной точки, также приводящее к изменению его движения. Если взаимодействующие друг с другом два тела имеют одинаковые массы, то они будут находиться в равных условиях, и, следовательно, силы, дей­ствующие на каждое из этих тел, будут одинаковы. Что же будет происходить при разных массах взаимодействующих тел? Ответ на этот вопрос дает третья аксиома динамики.

Аксиома 3 (третий закон Ньютона): силы взаимодейст­вия двух тел равны по величине, действуют вдоль одной пря­мой и направлены в противоположные стороны. Это положе­ние кратко формулируется так: действие равно и направлено противоположно противодействию.

Так как материальная точка может находиться в окру­жении многих тел, а каждое тело будет действовать на дан­ную точку с некоторой силой, возникает вопрос, какое уско­рение приобретает точка в этом случае. Если допустить, что действие нескольких сил на точку можно, как и в статике, заменить действием только одной силы — их равнодействую­щей, то задача отыскания ускорения решается сразу. Таким образом, приходим к четвертой аксиоме динамики.

Аксиома 4 (принцип независимости действия сил): уско­рение, приобретаемое материальной точкой при действии нескольких сил, равно геометрической сумме тех ускорений, которые имела бы точка при действии каждой силы в от­дельности.

Пусть на точку действуют п сил. Следуя второй и четвер­той аксиомам, имеем:

……………

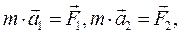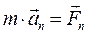
Складывая левые и правые части этих соотношений, по­лучаем

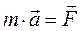(3.1)

где ,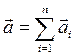

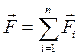
Таким образом, в правой части уравнения движения ма­териальной точки (3.1) стоит равнодействующая всех сил, действующих на эту точку.

Различают два типа движения точки: свободное и несво­бодное, когда на ее перемещения наложены ограничения, на­зываемые связями. На свободную точку действуют силы, ко­торые подчиняются определенным закономерностям; эти силы называются задаваемыми или активными. Так силы упругости и силы тяготения известным образом зависят от координат точки; силы сопротивления зависят от скорости движения точки; существуют активные силы, зависящие от времени(вынуждающие силы).

При несвободном движении материальной точки, наряду с задаваемыми силами, на нее действуют еще силы реакций связей, которые являются неизвестными и могут быть най­дены лишь. после определения закона движения самой точки. В этом случае, естественно, решение задачи усложняется.