Теорема о сложении скоростей в относительном движении.
Рассмотрим некоторую вектор-функцию 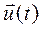 , проекции которой в относительной системе координат
, проекции которой в относительной системе координат 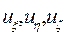 , являются заданными функциями времени, и сравним между собой векторные производные от этой функции, вычисленные наблюдателями в абсолютной и относительной системах координат. Для этого, замечая, что
, являются заданными функциями времени, и сравним между собой векторные производные от этой функции, вычисленные наблюдателями в абсолютной и относительной системах координат. Для этого, замечая, что 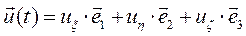 ,составим производную по времени от вектора
,составим производную по времени от вектора 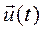 в абсолютной системе координат
в абсолютной системе координат
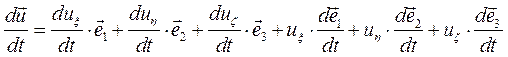 (2.33)
(2.33)
Первые три слагаемые в выражении (2.33), являются производной от вектора 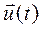 , вычисленной в предположении неизменности направления единичных векторов осей относительной системы координат.
, вычисленной в предположении неизменности направления единичных векторов осей относительной системы координат.
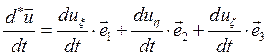
Такое выражение естественно назвать относительной производной. Для преобразования остальных слагаемых векторного выражения, вспомним формулу (2.24)-скорость вектора постоянного по модулю есть 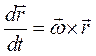 , откуда следует
, откуда следует 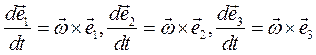 , где
, где 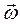 - вектор угловой скорости вращения относительной системы координат
- вектор угловой скорости вращения относительной системы координат 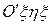 . Таким образом, равенство (2.23) приобретает вид
. Таким образом, равенство (2.23) приобретает вид
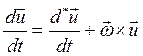 (2.34)
(2.34)
и мы приходим к следующей весьма важной для дальнейшего лемме: абсолютная производная по времени от вектора равна геометрической сумме относительной производной того же вектора и векторного произведения вектора угловой скорости вращения относительной системы координат на дифференцируемый вектор.
Применим доказанную лемму для вывода теоремы о сложении скоростей. С этой целью вычислим абсолютную производную по времени от обеих частей равенства (2.32) будем иметь:
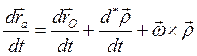
или 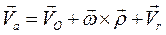 . (2.35)
. (2.35)
Но сумма первых двух слагаемых справа по известной формуле для скоростей точек твердого тела (формула 2.30) есть переносная скорость 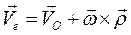 . Итак, окончательно получим
. Итак, окончательно получим
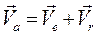 . (2.36)
. (2.36)
Абсолютная скорость точки равна геометрической сумме переносной и относительной скорости.
Дата добавления: 2016-01-07; просмотров: 880;
