Скорости и ускорения в общем случае движения

Твердого тела.

Перемещение любой точки тела, как было показано, скла­дывается из поступательного перемещения, равного перемеще­нию полюса, и вращательного вокруг оси, проходящей через полюс. Если рассматривать только бесконечно малые переме­щения тела, соответствующие переходу тела из данного поло­жения в бесконечно близкое, то с точностью до бесконечно малых высших порядков можно представить вращательное перемещение как векторное произведение вектора бесконечно малого поворота 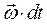на вектор-радиус 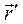рассматриваемой точки по отношению к полюсу.

.

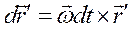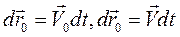
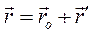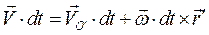Так как , то , где 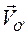-скорость полюса, разделив полученное выражение на 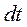, получим

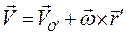. (2.30)

Эта основная формула кинематики твердого тела дает закон распределения скоростей в твердом теле в общем случае его движения.

Слагаемое 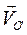определяет поступательную составляющую скорости, равную скорости по­люса, второе слагаемое представляет собой вращатель­ную составляющую скорости тела вокруг полюса О'.

Зная движение полюса и закон вращения тела вокруг по­люса, т. е. имея уравнения движения, можем по формуле (2.30) определить скорость любой точки тела. Проекции скорости на оси получим по общим правилам проектирования векторных выражений. Выпишем проекции скорости на неподвижные оси:

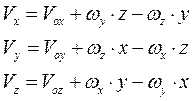
Здесь 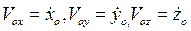Переходим к рассмотрению вопроса о распределении уско­рений. Для этого продифференцируем левую и правую части (49) по времени; получим

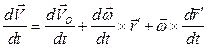
или

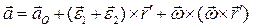(2.31)

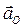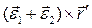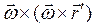Первое слагаемое определяет поступательное ускорение, равное ускорению полюса, а второе и третье: и - вращательную и центростремительную состав­ляющие ускорения вращения тела вокруг полюса. Таким образом, полу­чаем: ускорение точки твер­дого тела в общем случае его движения склады­вается из трех состав­ляющих: 1) поступатель­ного ускорения, одинакового в данный момент для всех точек тела и равного ускорению полюса; 2) вращательного ускорения вокруг полюса ( 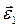направлено по мгновенной оси и характеризует изменение угловой скорости по величине, 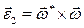- характеризует изменение угловой скорости по направлению и оно перпендикулярно мгновенной оси), 3) осе­стремительного ускорения, равного по величине произведению квадрата угловой скорости на кратчайшее расстояние точки до мгновенной оси вращения.

Глава 8.