Скорости и ускорения точек твердого тела, вращающегося вокруг неподвижного центра.

Формулу угловой скорости можно получить с помощью матрицы α. Пусть точка М определена в неподвижной системе вектором 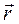, а в подвижной вектором 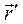, тогда можно записать 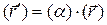или

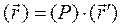, (2.26)

где 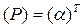. Продифференцируем (2.26) по времени

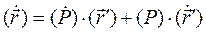. (2.27)

Второе слагаемое равно нулю, так как в подвижной системе вектор- столбец 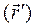постоянен. Перепишем (2.27) в таком виде

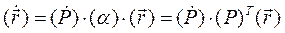
Матрицу 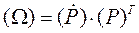назовём матрицей угловой скорости. Докажем, что эта матрица кососимметричная. Условие кососимметричности матрицы есть, 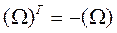. Заметим

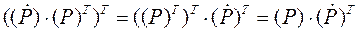
а также

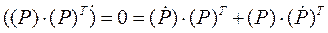
откуда получаем .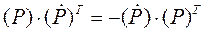

Известно, что для кососимметричной матрицы 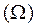существует сопряженный вектор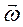

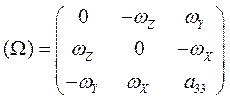
такой что 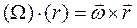, где 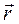- вектор столбец координат точек тела. Мы получили ту же формулу (2.24).

Перейдём к рассмотрению ускорений точек тела вращающегося вокруг неподвижной точки. По определению ускорение точки есть производная от вектора скорости

,

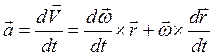Но по (2.25) имеем 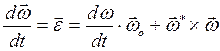и, учитывая что 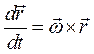, получим

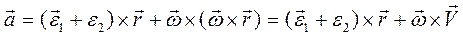(2.28)

Первое слагаемое 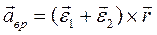- вращательное ускорение, которое не направлено в общем случае по вектору скорости, второе слагаемое 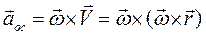- есть осестремительное ускорение, направленное всегда к мгновенной оси вращения и численно равно .

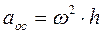Глава 6.