Кручение стержней открытого профиля
Рассмотрим. кручение стержней с прямоугольным сечением.

рис.18.29
Точное решение получено Сен-Венаном. Но можно получить приближенное решение и инженерными методами, считая, что стержень – это совокупность круглых валов, как это показано на рис.18.30.

рис.18.30
Введем систему координат 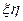 (см. рис. рис.18.29). Если считать, что напряжения не меняются по ширине рассматриваемого прямоугольника, а только по высоте, то получим:
(см. рис. рис.18.29). Если считать, что напряжения не меняются по ширине рассматриваемого прямоугольника, а только по высоте, то получим:
 . (18.28)
. (18.28)
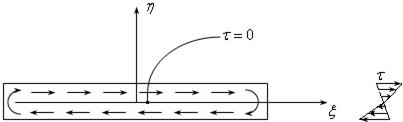
рис.18.31
Разбив площадь на микроплощадки и вычисляя силу 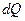 , которая действует на нее, можно подсчитать момент, который создает сила
, которая действует на нее, можно подсчитать момент, который создает сила 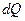 . Например, от горизонтальных напряжений момент будет
. Например, от горизонтальных напряжений момент будет
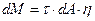 . (18.29)
. (18.29)
Приравнивая сумму всех моментов крутящему моменту можно найти выражение для 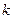 :
:
 . (18.30)
. (18.30)
Здесь: 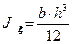 .
.
Формулу для 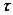 теперь можно записать в виде, аналогичном случаю круглых валов (см.формулу (18.5)):
теперь можно записать в виде, аналогичном случаю круглых валов (см.формулу (18.5)):
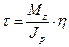 , где
, где 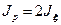 (18.31)
(18.31)
Для угла закрутки стержня прямоугольного сечения формула имеет вид:
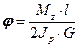 (18.32)
(18.32)
Здесь в отличие от круглых валов (см.формулу (18.10)) в знаменателе есть коэффициент 2.
Если стержень состоит из нескольких прямоугольников (см.рис.18.16), то выкладки (18.28) – (18.31) будут такими же. Изменится только момент инерции 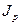 . Он будет состоять из суммы моментов каждого прямоугольника:
. Он будет состоять из суммы моментов каждого прямоугольника:
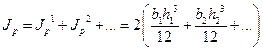 . (18.33)
. (18.33)
Сравнивая (18.31) с (18.19) можно заметить, что в отличие от тонкостенных стержней замкнутого профиля в стержнях с открытым профилем максимальные напряжения возникают там, где 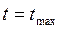 , т.е. там, где стенка является наиболее толстой. Значит и разрушение начнется в самом толстом месте сечения.
, т.е. там, где стенка является наиболее толстой. Значит и разрушение начнется в самом толстом месте сечения.
Отметим, что стержни с замкнутым профилем намного прочнее и жестче, чем стержни с открытки профилем. Для примера можно рассмотреть трубу квадратного сечения ширины а, постоянной толщины t (см. рис.18.28). Тогда 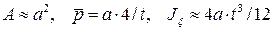 .
.
Вычислим напряжение и угол закрутки для трубы с замкнутым контуром:
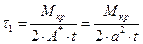 ,
, 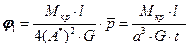 .
.
Если же разрезать трубу вдоль оси (например, вдоль ребра), то получим стержень с открытым контуром. Вычислим максимальное напряжение (которое будет при 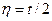 ) и угол закрутки. Учитывая, что
) и угол закрутки. Учитывая, что 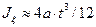 получим:
получим:
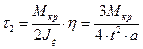 .
. 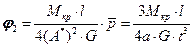 .
.
Найдем отношения напряжений и углов закрутки 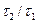 ,
, 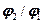 :
:
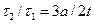 ,
, 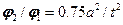 .
.
Видно, что при малых t напряжение 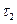 и угол
и угол 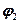 будут гораздо больше. Например, если положить а = 20 см., t = 1мм., то получим
будут гораздо больше. Например, если положить а = 20 см., t = 1мм., то получим
 ,
, 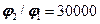 .
.
Можно сказать, что после разреза трубы прочность понизилась в 300 раз, а жесткость в 30000 раз.
Сложная деформация
Сложная деформация – это совокупность двух или более простых типов деформации бруса.
Их виды:
1) Растяжение с изгибом
2) Кручение с изгибом
3) Кручение с изгибом и растяжением
4) Растяжение с кручением
5) Косой изгиб (изгиб в двух плоскостях)
Дата добавления: 2015-11-28; просмотров: 845;
