Усилие растяжения (сжатия)

С этого раздела начинается введение новых понятий, специфических для дисциплины «сопротивление материалов». Первым важным является понятие под названием внутренний силовой фактор. Частным его случаем

Рис.2.2.1

является понятие усилие растяжения (сжатия).

Рассмотрим рис.2.2.1. Если для среднего стержня ответ на вопрос «чему равняется усилие растяжения?» является очевидным (оно равняется F), то для верхнего стержня этот вопрос обычно вызывает затруднения (часто говорят, что оно равно нулю или 2F). Однако третий нижний рисунок равносилен первым двум, поскольку реакция R=F. Таким образом, во всех этих случаях усилие растяжения равно F , поскольку схемы равносильны.

Сила растяжения обозначается буквой N. В нашем случае

N = F

Рассмотрим теперь рис.2.2.2. Можно ли сказать, чему равна сила растяжения? Нет, т.к. это равносильно тому, что спросить: «Чему равна ширина реки Волга»? В обоих случаях, нужно указывать – в каком месте.

Рис.2.2.2

Введем следующее определение. Разделим мысленно брус на две части сечением В-В.

Продольной силой N врассматриваемом внутреннем сеченииназовем равнодействующую всех внешних осевых сил, с которой левая часть воздействует на правую часть (или с которой правая часть воздействует на левую)

Примечания.

1). Синонимами термина «продольная сила»» являются термины нормальная сила, усилие растяжения, осевая сила.

2). Главная идея сопротивления материалов заключается именно в том, что тело считается состоящим из двух частей.

Это определение можно сформулировать как следующее правило для вычисленияN: продольная сила это сумма всех внешних осевых сил, которые лежат справа или слева от сечения.

Правило знаков.

Если внешняя сила действует на сечение растягивающим образом, то она дает вклад в N со знаком «+», если действует сжимающим образом, то она делает вклад в N со знаком «-».

Для того чтобы указать, на какое сечение действует продольная сила, сечение и N снабжаются номером и индексом. Например, так, как показано на рис.2.2.3

N1 = F - 3F N2 = - 3F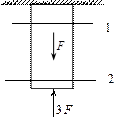

Рис.2.2.3

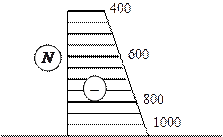
При наличии внешних погонныхсил осевая сила N зависит от положения сечения более сложным образом. Рассмотрим, например, задачу вычисления продольной силы с учетом силы тяжести (рис.2.2.4). Обозначим через q погонный вес бруса (для стандартных профилей прокатной стали, погонная масса приводится в таблицах сортамента). Пусть F = 400 Н, q = 200 Н/м. Рассмотрим сечение на расстоянии s от незакрепленного конца (см. рис.2.2.3). Тогда:

N = – F – qs

Задавая разные значения для s получим разные значения N (см. таблицу).

Зависимость N от положения сечения для наглядности представляют графически. График этой зависимости называется эпюрой N.

Рис.2.2.4

 

Правила графического изображения N.

1). Значения N откладываются перпендикулярно оси бруса.

2). Если усилие N является растягивающим, то ставится знак «+» (в нашем примере на рис.2.2.4 имеем отрицательный знак).

Метод сечений

Это метод, который позволяет определять N в сложных конструкциях типа стержневой системы, например, фермы. Суть метода рассмотрим на простом примере, приведенном на рис.2.3.1. Пусть длины стержней l₁=4м, l₂=5м, ВС=3м. Тогда ; .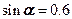

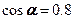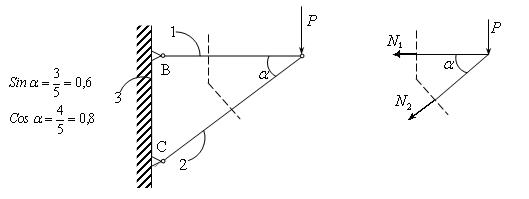
рис.2.3.1.

Найдем усилия растяжения.

Сделаем сечение, которое делит конструкцию на две части. Нарисуем правую часть. На нее левая часть действует силами .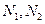

Конструкция в целом находится в покое, следовательно, любая её часть то же находится в покое, тогда для правой части можно записать уравнения равновесия:

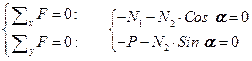
Отсюда, находим:

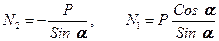
Анализ решения:

1) Видно, что первый стержень растягивается, так как N₁ >0, а второй стержень сжимается, так как N₂<0.

2) Чем меньше 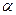, тем меньше 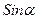, следовательно, тем больше 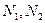, причем, 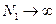, 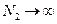при .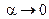

Резюмируя можно, что метод сечений заключается в следующем:

1) Конструкция делится на две части сквозным сечением.

2) В сечениях стержней изображаются внутренние силовые факторы (т.е. изображается - воздействие одной части конструкции на другую)

3) Записываются уравнения равновесия для одной из частей конструкции.

4) Проводится решение системы уравнений, и отыскиваются внутренние силовые факторы.