Потенциал. Разность потенциалов

Как известно, в случае потенциального поля

(3.11)

где W_p – потенциальная энергия.

Из формулы (3.8) работа по перемещению точечного заряда q₀ в поле заряда q

(3.12)

Из сравнения (3.11) и (3.12) следует, что потенциальная энергия заряда q₀ в поле точечного заряда q

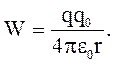(3.13)

Из (3.13) видно, что при r®¥ W_p обращается в ноль. Из (3.13) также видно, что W_p зависит от величины внешнего заряда и не является характеристикой поля.

Величина 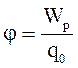не зависит от величины вносимого в поле заряда, она называется потенциалом поля в данной точке.

Для точечного заряда

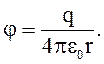(3.14)

Потенциал в точке, удаленной в бесконечность, равен нулю:

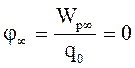при r®¥.

Выразим потенциал через работу A:

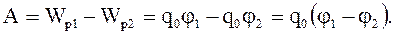(3.15)

Рассмотри два случая:

1. Заряд переносится из данной точки в бесконечность

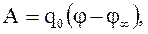
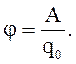(3.16)

2. Заряд переносится из первой точки во вторую

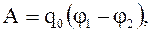
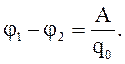т начального и конечного положения заряда зависитеское поле (рис.3.4). дна силовая линия, т.е. . равлению: т единичная сила:

ен

Разностью потенциалов называется физическая величина, численно равная работе по перемещению единичного положительного заряда из первой точки во вторую.

За единицу разности потенциалов принимают разность потенциалов между такими точками поля, при перемещении между которыми единицы заряда совершается единичная работа.

В СИ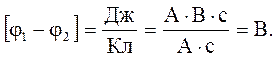

Принцип суперпозиции:

а) для дискретного распределения зарядов

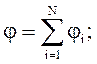(3.17)

б) для непрерывного распределения зарядов

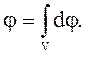(3.18)