Спектр бесконечной последовательности радиоимпульсов.
Бесконечная последовательность когерентных прямоугольных радиоимпульсов с монохроматическим заполнением на несущей частоте fн может быть представлена в следующем виде:
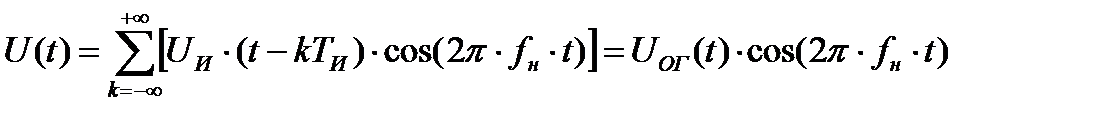
где Uи - функция, описывающая огибающую одиночного прямоугольного импульса;
Ти - период повторения (следования) импульсов;
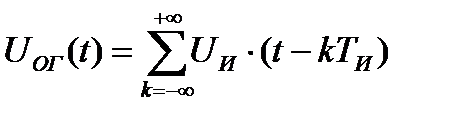 - бесконечная периодическая последовательность
- бесконечная периодическая последовательность
огибающих радиоимпульсов.
Определим спектральный состав последовательности U(t) , для чего разложим в ряд Фурье периодическую функцию Uог (t):
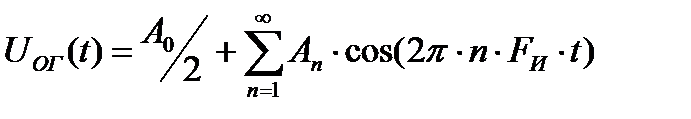
где Ао -постоянная составляющая,
Fи = 1/Tи - частота повторения (следования ) импульсов.
Амплитуды гармоник спектра последовательности прямоугольных импульсов равны:
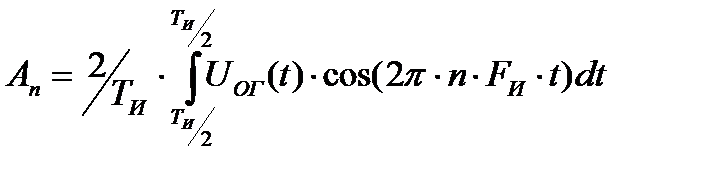
Тогда спектральный состав бесконечной последовательности прямоугольных когерентных радиоимпульсов примет следующий вид:
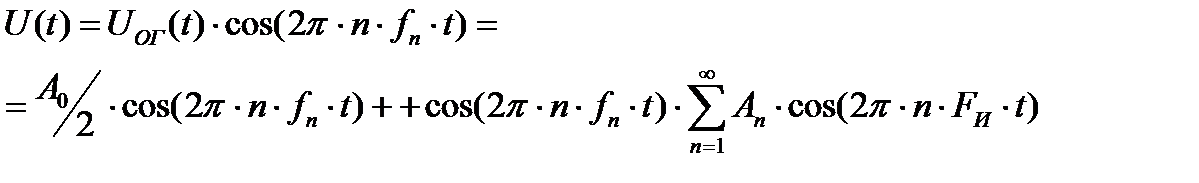
После разложения произведения косинусов во втором слагаемом окончательно получим:
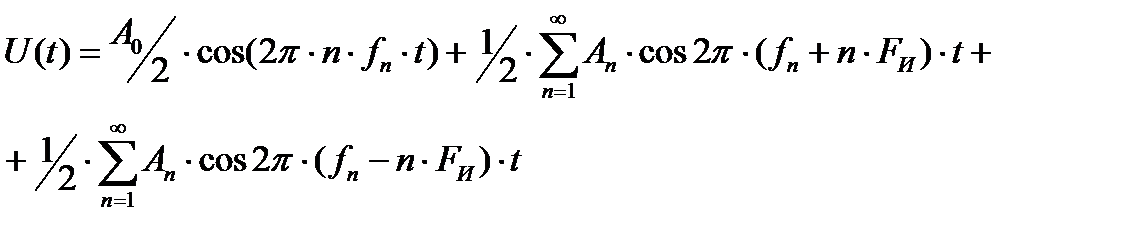
Таким образом, спектр бесконечной последовательности прямоугольных когерентных радиоимпульсов представляет собой бесконечную совокупность спектральных линий, соответствующих частотам fн ± nFи . Эта форма записи соответствует условию, при котором несущая частота fн кратна частоте повторения Fи. В общем случае несущая частота не кратна Fu; при этом составляющая Ао /2 Cos2pfнt в спектре отсутствует.
| Fи |
| Fн -2/τи |
| fн -1/τи |
| Fн+1/τи |
| Fн+2/τи |
| Fн |
| U |
| f |
| Δfс=2τи |
| Рис. 8.2. Спектр бесконечной последовательности прямоугольных когерентных импульсов |
Полученное спектральное представление означает, что полная энергия бесконечной последовательности прямоугольных когерентных радиоимпульсов распределена не равномерно по оси частот, а сосредоточена лишь на отдельных дискретных частотах. Таким образом, спектр носит дискретный характер, а дискретность определяется частотой следования импульсов Fu . Этот спектр носит линейчатый характер, который является следствием бесконечности последовательности импульсов.
Более того, полная энергия бесконечной последовательности радиоимпульсов распределена не равномерно между отдельными гармониками спектра. Как известно, огибающая дискретных гармоник определяется формой спектра одиночного импульса и представляет собой модуль функции
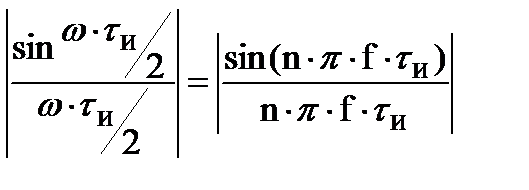
где tи - длительность одиночного импульса ;
f - аргумент этой функции , характеризующий отклонение от несущей частоты.
В точке fн аргумент f = 0; при f = m / tu , где m = ± 1 , 2 . функция обращается в нуль, т. е. нули огибающей спектра отстоят от несущей частоты на величину
m / tu .
Как видно из рисунка, энергия бесконечной последовательности импульсов сосредоточена главным образом в основном лепестке, т.е. в полосе частот Dfc= 2/tu; именно в этой полосе сосредоточено около 90 % всей энергии последовательности импульсов. В инженерной практике ширина спектра чаще оценивается не по нулям основного лепестка, а по уровню
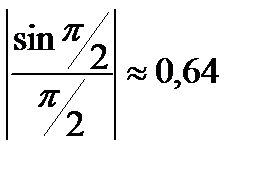 при этом ширина спектра
при этом ширина спектра 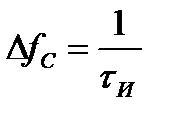
Количество спектральных линий в пределах ширины спектра определяется скважностью
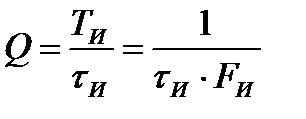
и может быть достаточно большим. Так, например, при tu = 1 мкс. и Fu = 1000 Гц в пределах ширины спектра укладывается 1000 гармоник. В связи с этим следует учитывать, что изображение спектра представленное на рисунке, носит условный характер.
Дата добавления: 2016-01-07; просмотров: 2630;
