Измеренных величин.
В практике геодезических измерений определяемые величины обычно являются функциями других, непосредственно измеряемых величин. Рассмотрим функцию u независимых переменных x, y, z, …
u = f (x,y,z…). (5.5)
Продифференцируем функцию (5.5) по всем переменным и заменим дифференциалы du, dx, dy, dz, …. погрешностями Du, Dx,Dy,Dz, ….
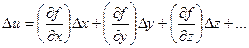
Получили выражение случайной погрешности Du в зависимости от случайной комбинации погрешностей Dx,Dy,Dz, …. Положим, что имеем n таких комбинаций, которым соответствует n выражений:
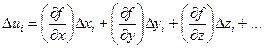 (i = 1, 2, …, n)
(i = 1, 2, …, n)
Возведем полученные выражения в квадрат, сложим и разделим на n:
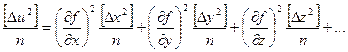
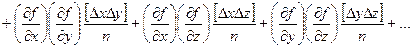 ,
,
где квадратными скобками обозначены суммы.
Устремим число комбинаций в бесконечность (n ® ¥) и, воспользовавшись выражениями (5.4) и (5.3), получим: 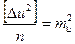 ,
, 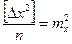 ,
, 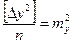 ,
, 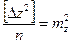 ,
, 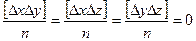 . И окончательно
. И окончательно
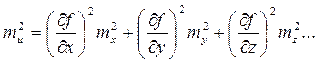 (5.6)
(5.6)
Итак, квадрат средней квадратической погрешности функции общего вида равен сумме квадратов произведений частных производных по каждой переменной, умноженных на их средние квадратические погрешности.
Частные случаи.
1. Функция u является суммой переменных x , y, z:
u = x + y + z.
В этом случае 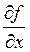 =1,
=1, 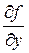 =1,
=1, 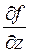 =1. Следовательно
=1. Следовательно
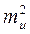 =
= 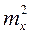 +
+ 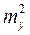 +
+ 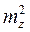 .
.
2. Функция u является разностью переменных x и y:
u = x - y.
В этом случае 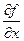 =1,
=1, 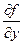 =-1. Следовательно
=-1. Следовательно
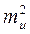 =
= 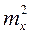 +
+ 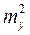 .
.
3. Функция u имеет вид:
u = k× x,
где k – постоянный множитель. Теперь 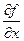 = k, поэтому
= k, поэтому 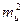 = k2×
= k2× 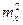 и
и
mu = k× mx.
4. Функция u является линейной функцией от x, y, z, …:
u = k1 x + k2 y + k3 z …,
где ki постоянные множители. Теперь частные производные равны 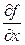 =k1,
=k1, 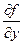 = k2,
= k2, 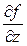 = k3. Поэтому
= k3. Поэтому
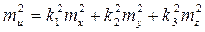 .
.
Рассмотрим примеры.
Пример 1. Определить среднюю квадратическую погрешность превышения, вычисленного по горизонтальному расстоянию d=124,16 м и углу наклона n=2°16´, если md = 0,06 м, а mn = 1´.
Превышение вычисляют по формуле
h = d tgν.
Продифференцируем формулу по переменным d и n:
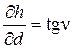 ,
, 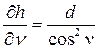 .
.
Используя формулу общего вида (5.6) получим
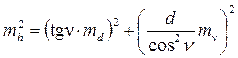
Подставляя исходные данные, найдем
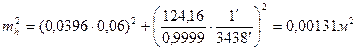
где 3438¢ - число минут в радиане. И окончательно mh=0,036 .м.
Пример 2. При геометрическом нивелировании (см. раздел 9.2) превышение вычисляют как разность отчетов по рейкам
h = a - b.
Отчеты берут с точностью ma = mb = 2 мм. Находим среднюю квадратическую погрешность превышения
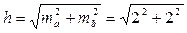 = 2,8 мм
= 2,8 мм
Пример 3. Выведем формулу допустимой угловой невязки замкнутого теодолитного хода (см. раздел 9.4). Невязку вычисляют по формуле
fb= b1+ b2+ ¼+ bn-180°(n-2),
где bi – измеренные углы (i = 1, 2, ¼, n) и n – их число.
Невязка - результат погрешностей в углах bi. Поэтому средняя квадратическая погрешность невязки равна
mf = 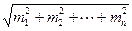 =
= 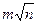 ,
,
где m1 = m2 =¼ = mn = m – средняя квадратическая погрешность измерения угла. Примем ее равной m = 0,5¢.
Допуском угловой невязки (fb)доп служит предельная погрешность (fb)пред=2mf. Получаем формулу
(fb)доп = 1¢ 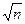 .
.
Дата добавления: 2016-01-03; просмотров: 688;
