Теорема Вариньона о моменте равнодействующей
Пространственная система сил приведена к равнодействующей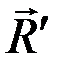 
в точке О (рис. 43), значит, главный момент системы сил 
.
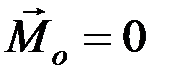| Рис. 43 |
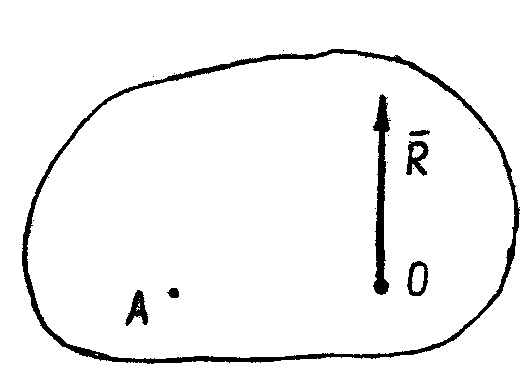Тогда, согласно выражению (2.29), главный момент этой системы относительно нового центра А равен 
.
Согласно выражению (2.13),
Окончательно получается
(2.30)
Равенство (2.30) выражает теорему Вариньона о моменте равнодействующей относительно центра.
Момент равнодействующей пространственной системы сил относительно любого центра А равен геометрической сумме моментов всех сил относительно этого центра.
Спроектировав векторное равенство (2.30) на координатные оси, например на ось Ox, получаем выражение (2.31) теоремы Вариньона о моменте равнодействующей относительно оси:
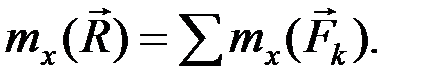(2.31)
Момент равнодействующей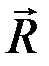 
относительно оси равен алгебраической сумме моментов всех сил относительно этой оси.
Частный случай теоремы Вариньона для плоской системы сил.
Так как для плоской системы сил моменты на плоскости суммируются алгебраически (см. выражение (2.9)), то теорема Вариньона о моменте равнодействующей 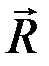относительно центра А имеет вид:
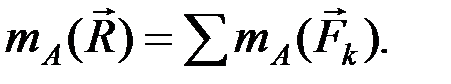(2.32)
Момент равнодействующей плоской системы сил относительно любого центра А равен алгебраической сумме моментов всех сил относительно этого центра.
Дата добавления: 2016-01-03; просмотров: 879;