Оценка точности линейных построений
При использовании лазерных измерительных приборов обеспечивается миллиметровая точность результатов. На первый взгляд может создаться впечатление, что точность положения обеспечена во всех случаях. Но это далеко не так.
Пусть непосредственно измерены величины длин линий l1 и l2 , точность которых нам известна и составляет m1 и m2.
Если координаты наблюдаемого пункта представить в виде функции f от аргументов l1 и l2 , то для средней квадратической ошибки этой функции будет иметь место зависимость:
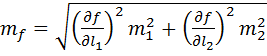 . (1.23)
. (1.23)
Если предположить, что все измерения равноточные
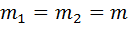 ,
,
то выражение (4.10) упростится и примет вид
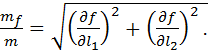 . (1.24)
. (1.24)
Относительная погрешность определения абсциссы составит :
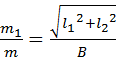 . (1.25)
. (1.25)
Относительная погрешность определения ординаты составит:
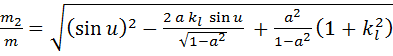 , (1.26)
, (1.26)
где
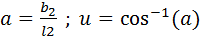 ;
; 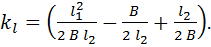
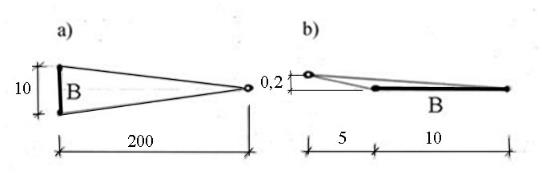
Рис. 1.13. Неустойчивые конфигурации линейных построений
Существуют различные неустойчивые конфигурации линейных построений. Две из них, в качестве примеров, приведены на рисунке 4.8.
При точности линейных измерений (с учётом погрешности центрирования ) в 10 мм ошибка абсциссы в первой точке (см. рис. 1.13,а) составит 280 мм, а ошибка ординаты во второй точке 450 мм (см. рис. 1.13,б).
Из приведенных примеров следует, что погрешности определения прямоугольных координат, даже при использовании точных лазерных приборов, при определённых условиях будут недопустимы.
Дата добавления: 2016-01-03; просмотров: 1134;
