Расчет сжато-изгибаемых элементов
Многие элементы деревянных конструкций работают в условиях сжатия с изгибом: арки, элементы рам, стойки и колонны, верхние пояса стропильных ферм при наличии внеузловой нагрузки.
Расчет сжато - изгибаемых элементов должен производиться по деформируемой схеме, т.к. в этом случае наряду с поперечным изгибом возникает (вследствие прогибов) продольный изгиб (элемент работает в условиях продольно-поперечного изгиба) (рис.2. 12). Под действием поперечной нагрузки q элемент прогибается, при этом продольная сила создает дополнительных изгибающий момент MN, который в свою очередь вызывает дополнительных прогиб сечений элемента, что приводит к еще большему возрастанию результирующего момента.
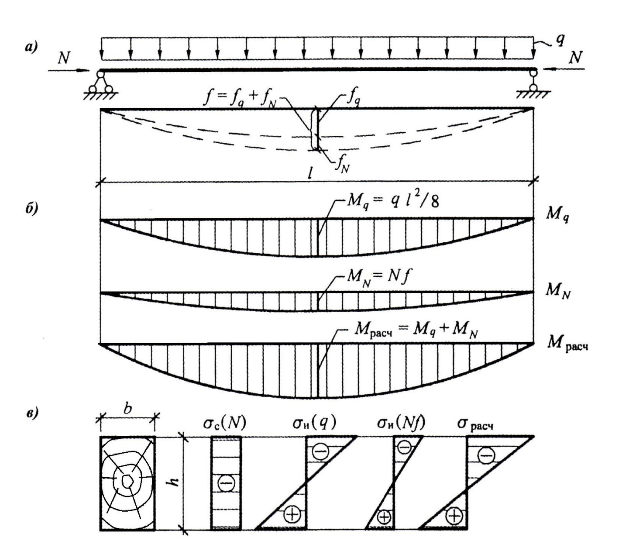
Рис. 2.12. Сжато-изгибаемые элементы: а - схема работа элемента;
б – эпюры изгибающих моментов; в – эпюры напряжений
Полный изгибающий момент Mд, определяемый с учетом формирования стержня, можно представить в следующем виде:
 (2.26)
(2.26)
где Mq - изгибающий момент оси действия поперечных нагрузок;
Mq - изгибающий момент, вызываемый действием поперечных нагрузок;
MN - изгибающий момент, вызываемый действием продольной силы;
𝜉 - коэффициент, учитывающий дополнительный момент от действия продольных сил при деформации стержня. Коэффициент 𝜉 определяется по формуле

где N - значение продольной силы в расчетном сечении;
Fбр - площадь расчетного сечения;
Rc - расчетное сопротивление материала сжатию;
φ - коэффициент продольного изгиба, определяемый по формулам (2. 12 или 2.13).
Разрушение сжато - изогнутого стержня может произойти при сохранении первоначальной формы равновесия элемента. В этом случае выполняется расчет на прочность по выражению

Кроме того, при сжатии с изгибом деревянного элемента может произойти потеря его устойчивости.
При центральном сжатии стержня проверку устойчивости можно представить в виде
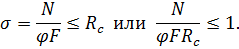
при изгибе условие устойчивости плоской формы балки
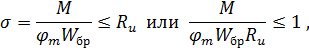
При совместном действии продольной сжимающей силы и изгибающего момента условие устойчивости элемента можно представить в виде следующей формулы:
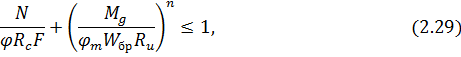
где φm - коэффициент устойчивости при изгибе балки, определяемый по выражению (2.19 );
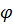 - коэффициент продольного изгиба, определяемый по гибкости участка элемента с расчетной длиной lp из плоскости деформирования;
- коэффициент продольного изгиба, определяемый по гибкости участка элемента с расчетной длиной lp из плоскости деформирования;
Rс и Rи - расчетные сопротивления древесины соответственно сжатию и изгибу;
n - показатель степени, зависящий от наличия закреплений растянутой зоны элемента плоскости деформирования элемента; n=1 для элементов, имеющих раскрепления растянутой кромки из плоскости деформирования и n=2 для элементов не имеющих такие закрепления.
При наличии в элементе на участке lp закреплений из плоскости деформирования со стороны растянутой от момента кромки, коэффициент φm следует умножить на коэффициент КПМ, определяемый по формуле (2.20), а коэффициент φ - на коэффициент KПN, который равен
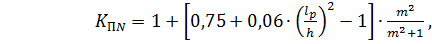 (2.30)
(2.30)
В этой формуле значения lp, m определяются согласно выражениям (2.13) и (2.14).
Дата добавления: 2016-01-03; просмотров: 9659;
