Расчет изгибаемых элементов при плоском изгибе
При поперечном (плоском) изгибе в поперечных сечениях элемента возникают изгибающие моменты и поперечные силы. Брус, работающий на изгиб называется балкой. К изгибаемым элементам относятся прогоны, плиты покрытий, балки покрытий и др.
Наиболее характерный случай нагружения балки представлен на рис.2.7.
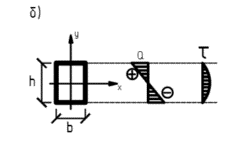
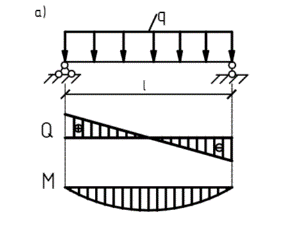
Рис.2.7 Поперечных изгиб балки: а-эпюры внутренних усилий; б-эпюры распределения нормальных и касательных напряжений в сечении балки
Нормальные напряжения в балке, вызываемые действием изгибающих моментов, определяются по зависимости
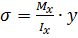 . (2.14)
. (2.14)
Касательные напряжения в поперечном сечении балки вычисляются по формуле Д.И. Журавского
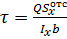 , (2.15)
, (2.15)
В формулах (2.13 и 2.14) М и Q – внутренние усилия в сечении элемента;
Ix– момент инерции сечения относительно нейтральной оси x;
Sxотс – статический момент относительно оси x отсеченной части сечения;
b – расчетная ширина сечения.
Основные условия прочности изгибаемого элемента можно представить в виде:
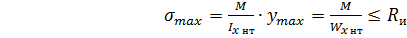 , (2.16)
, (2.16)
где Ixнти Wxнт=Ixнт/ ymax– соответственно момент инерции и момент сопротивления сечения нетто (ослабления расположенные на участке длины до 200 мм, принимают совмещенными в одном сечении);
Rи- расчетное сопротивление древесины изгибу.
Помимо расчета на прочность балки по нормальным напряжениям ее следует рассчитывать и на действие касательных напряжений. Сопротивление древесины перерезыванию волокон выше сопротивления древесины на скалывание вдоль волокон, поэтому проверка прочности по касательным напряжениям сводится к расчету древесины на скалывание вдоль волокон. Скалывание древесины вдоль волокон вызывается касательными напряжениями, действующими на продольных площадках (рис.2.8)
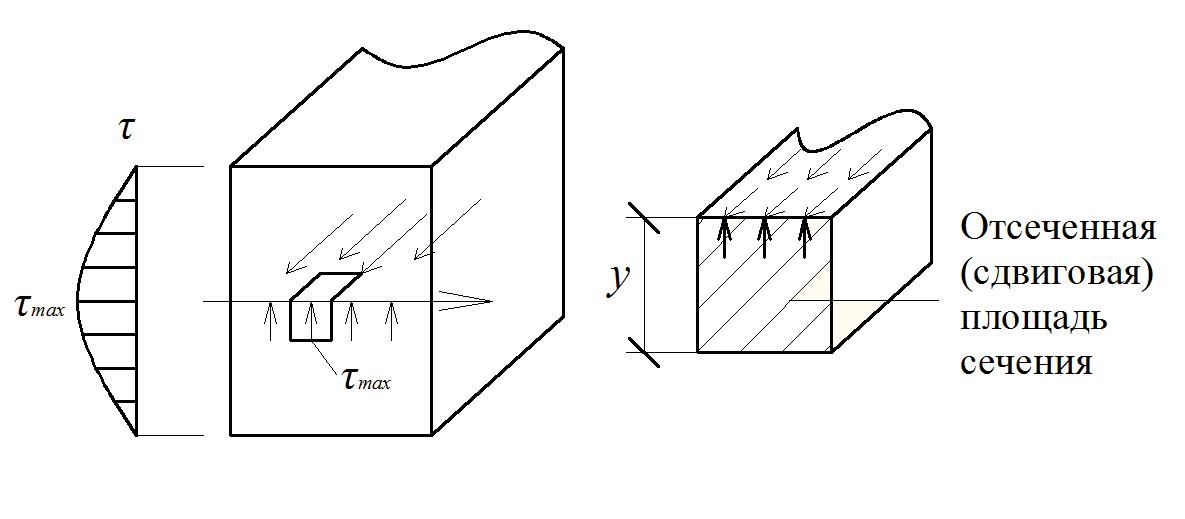
Рис. 2.8. Распределение касательных напряжений
в изгибаемом элементе
Условие прочности элемента на скалывание
 , (2.17)
, (2.17)
где Sx– статический момент брутто отсеченной (сдвигаемой) части сечения относительно нейтральной оси x;
Iбр – момент инерции сечения брутто;
Rск – расчетное сопротивление древесины на скалывание вдоль волокон.
Помимо выше приведенных расчетов на прочность изгибаемые элементы (особенно при их малой ширине – h/b > 4) проверяются на устойчивость плоской формы деформирования по формуле
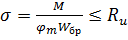 , (2.18)
, (2.18)
где M- максимальный изгибающий момент на рассматриваемом участке lp;
W – момент сопротивления сечения брутто;
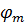 – коэффициент устойчивости элемента при изгибе.
– коэффициент устойчивости элемента при изгибе.
Коэффициент 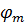 равен (для изгибаемых прямоугольных элементов)
равен (для изгибаемых прямоугольных элементов)
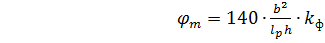 , (2.19)
, (2.19)
В этой формуле b и h –размеры поперечного сечения;
lp– расстояние между точками закрепления сжатой (от момента М) кромки элемента от смещения из плоскости изгиба (при отсутствии закрепления сжатой кромки в промежуточных точках lp=1);
kф – коэффициент, зависящий от формы эпюры моментов на участке lp.
Величина коэффициента kф определяется по таблицам СНиП [1], для случая, представленного на рис.2.7, коэффициент kф =1,13; (при М=const; kф =1).
При расчете изгибаемых элементов с линейно меняющейся по длине высотой и постоянной шириной поперечного сечения (например двускатные балки), не имеющих закреплений из плоскости по растянутой от момента М кромке, или при числе точек закрепления m < 4 (рис.2.9.) коэффициент 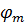 следует умножать на дополнительный коэффициент Кпм, который равен
следует умножать на дополнительный коэффициент Кпм, который равен
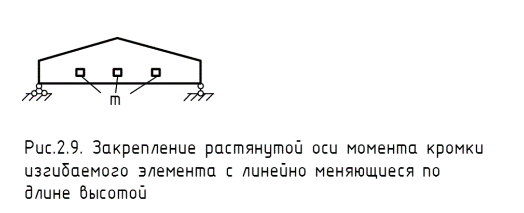
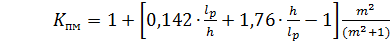 , (2.20)
, (2.20)
где m – число подкрепленных (с одинаковым шагом) точек (кроме опорных закреплений) на участке lp. При m ≥ 4 значение m2/(m2+1) следует принимать равным 1.
Расчет изгибаемых элементов на жесткость (по второй группе предельных состояний) ведется по нормативным нагрузкам по условию
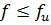 (2.21)
(2.21)
где f - расчетный (фактический) прогиб балки;
fu – предельный прогиб, установленный нормами.
Наибольший (расчетный) прогиб вычисляется по формуле
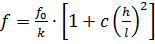 , (2.22)
, (2.22)
где 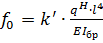 - прогиб элемента без учета деформации сдвига;
- прогиб элемента без учета деформации сдвига;
k  – коэффициент, зависящий от вида нагрузки, (при действии нагрузки qH=const величина k
– коэффициент, зависящий от вида нагрузки, (при действии нагрузки qH=const величина k  =5/384;
=5/384;
qH– нормативная нагрузка на балку;
k – коэффициент, учитывающий влияние изменения высоты сечения по длине;
c – коэффициент, учитывающий влияние деформации сдвига от поперечной силы. Значения коэффициентов k и c представлены в нормах [1]. Для балок постоянного сечения h=const и при qH=const значения этих коэффициентов равны k=1; c =19,2.
Дата добавления: 2016-01-03; просмотров: 3368;
