Расчет элементов при косом изгибе

В этом случае в поперечных сечениях рассчитываемого элемента возникают изгибающие моменты M_x и М_y относительно главных центральных осей сечения x,y. Например, в наклонных кровлях в прогонах прямоугольного сечения направление нагрузки не совпадает с направлением главных осей сечения (рис. 2.10). В этом случае действующее усилие q раскладывается по направлению главных осей сечения и определяются изгибающие моменты M_x и М_y.

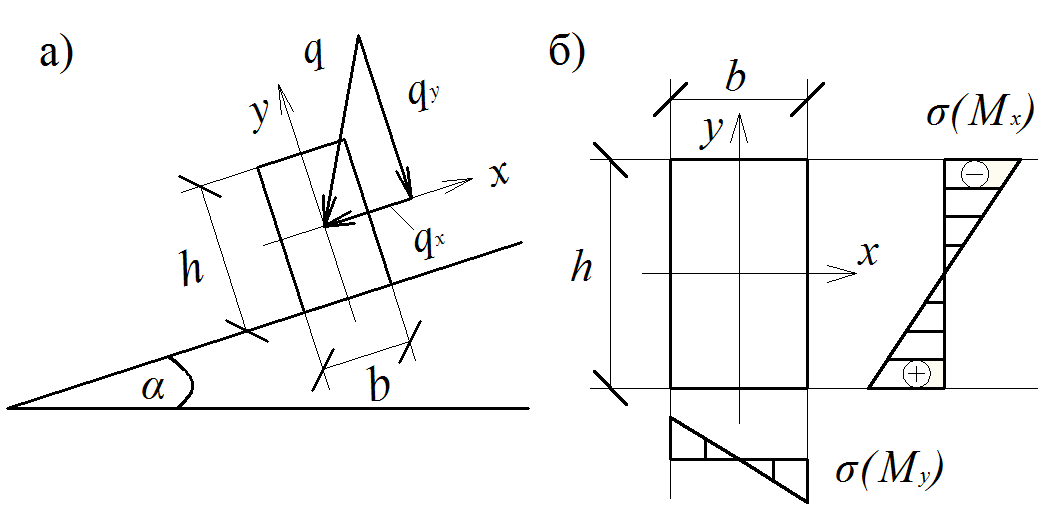
Рис. 2.10. Косой изгиб прогона:

а- схема работы; б- эпюра напряжений

Проверка прочности при косом изгибе выполняется по формулам

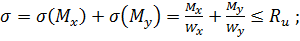(2.22)

где W_xи W_y - моменты сопротивления поперечного сечения нетто относительно главных центральных осей сечения.

Если поперечное сечение бруса круглое или квадратное (в этом случае осевые моменты инерции относительно всех центральных осей одинаковы), то при возникновении изгибающих моментов относительно осей x и y (см. рис. 2.11) косого изгиба не возникает. В этом случае результирующий изгибающий момент M_и равен: 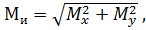который приводит к изгибу элемента в плоскости, проходящей через главную ось сечения u.

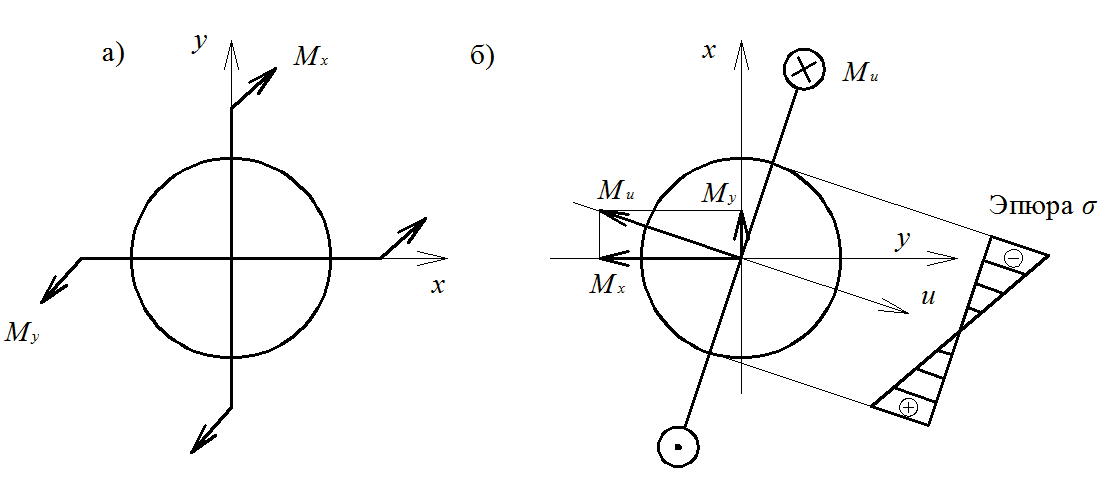
Рис. 2.11. Изгиб элемента круглого сечения: а – схема действия моментов от нагрузки в двух плоскостях; б – определение результирующего изгибающего момента Mи в векторной форме и эпюра напряжений

Напряжения в таком случае определяются как в случае плоского изгиба

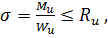(2.24)

где W_u - момент сопротивления сечения относительно главной оси u.

Расчет на жесткость при косом изгибе выполняется по полному прогибу f

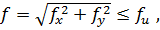(2/25)

где f_x и f_y - прогибы балки в направлении осей х и y;

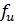- допускаемый прогиб.