Замкнутой САУ называют систему, в которой процесс управления ОУ зависит от результата управления. 4 страница
В дальнейшем для характеристики звена будет использоваться понятие передаточной функции, так как именно она дает связь между входной и входной переменными того или иного звена в САУ или всей системы в целом. Функция, связывающая один входной и один выходной сигналы САУ. Является формой записи системы дифференциальных уравнений САУ реш¨нной относительно требуемой выходной координаты. Обычно передаточные записывается не для временного домена, а для домена Лапласа, связывая в этом варианте не сигналы (т.е. не функции времени), а их изображения.
Для дифференциальных уравнений с нулевыми начальными условиями целесообразно применение преобразования Лапласа, которое выполняется с помощью выражения вида
 ,
,
где 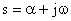 — комплексная переменная.
— комплексная переменная.
Важным свойством преобразования Лапласа является замена операций интегрирования и дифференцирования делением и умножением на оператор Лапласа соответственно. То есть имеют место следующие соотношения:
 .
.
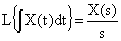
При переходе к преобразованию Лапласа рассматриваются не временные функции входной и выходной переменной, а их изображению по Лапласу. Применяя преобразование Лапласа к дифференциальному уравнению, описывающему поведение звена в динамических режимах, получаем
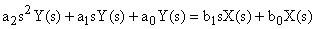
где  – оператор Лапласа.
– оператор Лапласа.
Теперь можно математически строго записать связь между изображениями входной и выходной величин

Передаточной функцией звена или САУ 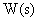 называется отношение изображений по Лапласу переменных на выходе и входе динамического звена. Согласно определению передаточная функция определяется как
называется отношение изображений по Лапласу переменных на выходе и входе динамического звена. Согласно определению передаточная функция определяется как
 .
.
Для получения передаточной функции необходимо дифференциальное уравнение, описывающее поведение системы или звена в динамических режимах. При заданной временной характеристики системы возможно использование таблиц, приведенных в различных учебниках по ТАУ и справочниках, связывающих 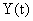 и
и 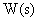 .
.
Передаточная функция может быть использована для решения широкого круга задач анализа и синтеза систем автоматического управления. С ее помощью можно определить как установившееся значения искомой переменной, так и проводить ее исследование в частотной и временной областях.
Использование передаточной функции для определения установившегося значения координат в САУ. Для этого необходимо определить значение изображения искомой переменной для случая, когда оператор Лапласа равен нулю.
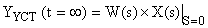 .
.
Расчет переходных процессов с использованием передаточной функции. Для отыскания оригинала искомой переменной по его изображению проводится с использованием теоремы разложения. Если изображение Лапласа представить в виде отношения двух многочленов
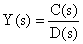 ,
,
то оригинал определяется по формуле вида:
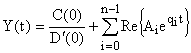 ,
,
где 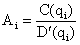 ,
,
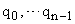 – корни характеристического уравнения вида
– корни характеристического уравнения вида 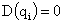 .
.
Понятие передаточной функции САУ используется при применении метода пространства состояний. Для определения специфики понятия передаточной рассмотрим уравнение (7). После выполнения преобразования Лапласа получаем
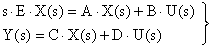 ,
,
где Е – единичная матрица.
Из этого уравнения следует, что изображение вектора состояния САУ определяется как
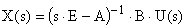 .
.
Тогда взаимосвязь между вектором входных сигналов и вектором состояния САУ определяется как
 .
.
Эта взаимосвязь и называется передаточной функции САУ в терминах пространства состояний. Она представляет собой матрицу, размерности 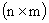 , каждый элемент которой
, каждый элемент которой 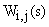 является передаточной функцией для компоненты вектора состояния с номером I относительно компоненты вектора входных сигналов с номером j.
является передаточной функцией для компоненты вектора состояния с номером I относительно компоненты вектора входных сигналов с номером j.
Вектор выходных сигналов САУ с учетом вышесказанного определяется как
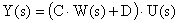 .
.
При этом выражение, стоящее в скобках, является передаточной функцией САУ, связывающей вектор ее выходных сигналов с вектором внешних воздействий.
Представление САУ в частотной области
Важную роль при описании линейных стационарных систем играют частотные характеристики. Если на вход линейной САУ подать синусоидальное воздействие, то по истечении некоторого времени, когда затухнут все движения, определяемые переходными процессами внутри САУ, на выходе системы установится также гармоническое изменение выходной координаты с той же частотой, которую имеет входная величина, но с иными амплитудами и фазой. Эти величины при прочих равных условиях, будут зависеть от частоты возмущающего воздействия. Такие зависимости называют частотными характеристиками САУ. По частотным характеристикам можно судить о динамических свойствах САУ. Для линейных систем справедлив принцип суперпозиции, то есть реакция системы на несколько одновременно действующих воздействий равна сумме реакций на каждое воздействие в отдельности. Это позволяет рассматривать частотные характеристики отдельно для каждого возмущения.
Периодическое гармоническое воздействие на объект может быть записано в векторной форме как
 ,
,
где Х – амплитуда воздействия,
 – угловая частота,
– угловая частота,
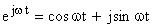 - единичный вектор.
- единичный вектор.
Послу затухания собственных колебаний в САУ на ее выходе установятся периодические колебания, определяемые выражением вида:
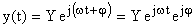 ,
,
где  — фазовый сдвиг выходного сигнала относительно входного.
— фазовый сдвиг выходного сигнала относительно входного.
Как действительные, так и векторное представление соотношения входных и выходных сигналов САУ показано на рис. 6.

Рис. 6. Входные и выходные сигналы САУ
В этом случае можно говорить о комплексном коэффициенте передачи САУ  , который определяется как
, который определяется как
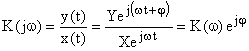 ,
,
где 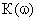 – модуль комплексного коэффициента передачи,
– модуль комплексного коэффициента передачи,
 — фаза вектора комплексного коэффициента передачи
— фаза вектора комплексного коэффициента передачи
Заметим, что если вместо подстановки сигналов записать дифференциальные уравнения движения системы для преобразования Лапласа и вновь найти отношение выходного сигнала к входному, то полученная, в ходе этого преобразования, передаточная функция совпадет с частотной передаточной функцией. Следовательно, можно отметить две особенности частотной передаточной функции:
во-первых, частотная передаточная функция получается из обычной заменой оператора Лапласа  на комплексную частоту
на комплексную частоту 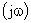 , т.е. в результате перехода от изображения Лапласа к изображению Фурье,
, т.е. в результате перехода от изображения Лапласа к изображению Фурье,
во-вторых, если дифференциальные уравнения движения системы связывает входной и выходной сигналы (т.е. функции времени), а передаточная функция связывает изображения Лапласа тех же сигналов, то частотная передаточная функция связывает их спектры
Комплексный коэффициент передачи является комплексной величиной, а его компоненты зависят от частоты входного сигнала. Модуль может быть представлен вектором на комплексной плоскости, как это показано на рис. 7.

Рис. 7. Характеристики комплексного коэффициента передачи.
При непрерывном изменении частоты происходит изменение положения вектора комплексного коэффициента передачи САУ, сопровождающееся изменением его модуля и фазы. Конец вектора описывает на комплексной плоскости некоторую кривую, называемую годографом. Годограф — это геометрическое место точек конца вектора комплексного коэффициента передачи на комплексной плоскости при изменении частоты от 0 до 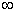 . Значения частот откладываются непосредственно на годографе, который является амплитудно-фазовой характеристикой системы (АФЧХ). Для определения модуля и фазы комплексного коэффициента передачи на заданной частоте следует соответствующую точку годографа соединить прямой с началом координат. Длина полученного отрезка соответствует модулю комплексного коэффициента передачи. Угол, образованной полученной прямой с положительной вещественной осью, является фазой комплексного коэффициента передачи (рис. 6). Такое представление частотной характеристики САУ достаточно наглядно, но не позволяет просто получать количественные характеристики для сравнения разных систем.
. Значения частот откладываются непосредственно на годографе, который является амплитудно-фазовой характеристикой системы (АФЧХ). Для определения модуля и фазы комплексного коэффициента передачи на заданной частоте следует соответствующую точку годографа соединить прямой с началом координат. Длина полученного отрезка соответствует модулю комплексного коэффициента передачи. Угол, образованной полученной прямой с положительной вещественной осью, является фазой комплексного коэффициента передачи (рис. 6). Такое представление частотной характеристики САУ достаточно наглядно, но не позволяет просто получать количественные характеристики для сравнения разных систем.
Для решения этой задачи используются:
Амплитудно-частотная характеристика САУ  – зависимость модуля комплексного коэффициента передачи от частоты.
– зависимость модуля комплексного коэффициента передачи от частоты.
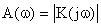
Вещественная частотная характеристика 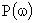 – зависимость действительной части комплексного коэффициента передачи от частоты:
– зависимость действительной части комплексного коэффициента передачи от частоты:
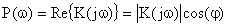
Мнимая частотная характеристика  – зависимость мнимой части комплексного коэффициента передачи от частоты:
– зависимость мнимой части комплексного коэффициента передачи от частоты:

Эти характеристики связаны между собой и вектором комплексного коэффициента передачи следующими зависимостями:
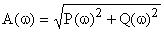 ,
,
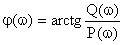 .
.

Рис. 8. Амплитудно-фазовая частотная характеристика
Другой формой представления частотных характеристик является логарифмическая амплитудно-частотная характеристика (ЛАЧХ) и логарифмическая фазовая частотная характеристика (ЛФЧХ). В этом случае по оси абсцисс откладывается частота в логарифмическом масштабе, что позволяет отложить на заданном отрезке значительный диапазон частот. Для комплексного коэффициента передачи определяется десятичный логарифм
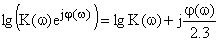 .
.
Из этого выражения следует, что комплексный коэффициент передачи может быть представлен совокупностью ЛАЧХ, определяемой как
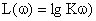 ,
,
и ЛФЧХ, совпадающей с 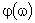 .
.
По оси абсцисс откладывается величину 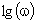 . При этом вводятся две единицы измерения:
. При этом вводятся две единицы измерения:
декада – длина отрезка, соответствующего десятикратному изменению частоты входного сигнала;
октава – длина участка оси частот, соответствующая двухкратному изменению частоты.
Фаза откладывается по оси частот в радианах или угловых градусах. Ординатой ЛАЧХ является не величина 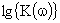 , а пропорциональная ей величина в децибелах
, а пропорциональная ей величина в децибелах
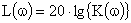 .
.
Использование логарифмического масштаба обусловлено не только значительными изменениями модуля комплексного коэффициента передачи. В большей степени это обусловлено возможностью выполнения графических методов расчета. При расчетах САУ часто приходится иметь дело с последовательным соединением элементов САУ. В этом случае комплексный коэффициент передачи определяется произведением отдельных коэффициентов передачи. А так как логарифм произведения есть сумма логарифмов сомножителей, то вычисления результирующей характеристики значительно упрощаются.
Рассмотрим САУ, числитель и знаменатель передаточной функции которой могут быть представлены либо в виде отношения полиномов:
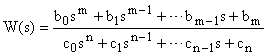 ,
,
либо в виде отношения их разложений на элементарные множители:
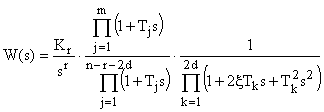
Постановка 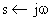 позволяет перейти в частотный область. При наличии ЭВМ построение ЛАЧХ и ЛФЧХ не составит труда в любом случае. Пример расчета логарифмических частотных характеристик САУ показан на рис. 9.
позволяет перейти в частотный область. При наличии ЭВМ построение ЛАЧХ и ЛФЧХ не составит труда в любом случае. Пример расчета логарифмических частотных характеристик САУ показан на рис. 9.
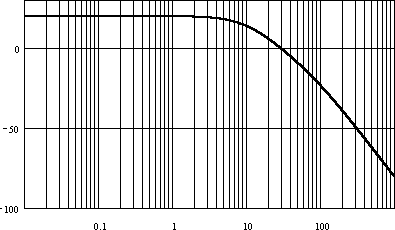

Рис. 9. ЛАЧХ и ЛФЧХ САУ.
Однако разложенная на множители передаточная функция позволяет построить асимптотические ЛАЧХ и ЛФЧХ практически без вычислительной работы. Каждый линейный множитель ее числителя и знаменателя есть комплексное число. Найдем модуль каждого (как гипотенузу прямоугольного треугольника), и перейдем к логарифмическому масштабу:

Для упрощения дальнейших построений избавимся от операции умножения, заменив ее операцией сложения в логарифмическом домене:
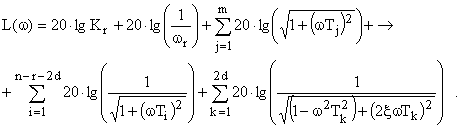
| (9) |
Легко понять, что каждое слагаемое этого выражения есть либо прямая линия, либо асимптотически приближается к прямым линиям при устремлении частоты к нулю и к бесконечности. Наклон аппроксимирующих прямых всегда кратен 20 дБ за декаду.
Для построения ЛФЧХ необходимо найти фазу каждого множителя числителя и знаменателя частотной передаточной функции, как арктангенс отношения его противолежащего катета к прилежащему (напомним, что при произведении комплексных чисел (в экспоненциальной форме) фазы (показатели степени) складываются, а при делении — вычитаются). Таким образом, построение ЛФЧХ производится по выражению:
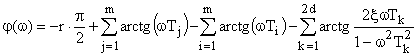
Отметим так же, что одному Белу соответствует увеличение мощности в 10 раз. Поскольку A - это физическая величина либо первого, либо второго рода, а не их произведение (т.е. не мощность); увеличение ее в 10 раз соответствует увеличению мощности в 100 раз, что соответствует двум Белам или 20 дБ.
Правила построения асимптотических ЛАЧХ и ЛФЧХ, точнее каждого слагаемого выражения (9) показаны на рис. 10.
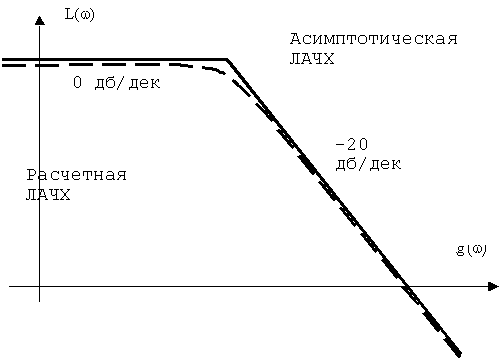
Рис. 10. Построение асимптотической ЛАЧХ.
Точность асимптотических ЛАЧХ и ЛФЧХ достаточна в большинстве случаев. Для звеньев первого порядка максимальная амплитудная ошибка вблизи частоты сопряжения составляет 3 дБ. Максимальная фазовая ошибка — 6%. Фрагмент частотной характеристики колебательного звена вблизи резонансной частоты лишь иногда следует уточнить по опорным справочным кривым для данного 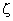 .
.
Вопросы
1. Что называется моделью САУ?
2. Что понимается под понятием динамические режимы работы САУ?
3. Какой математический аппарат используется для анализа динамических режимов работы САУ?
4. Как записать дифференциальное уравнение движения в операторной форме?
5. Что называется операторной формой записи дифференциального уравнения?
6. Что вы понимаете под пространством состояния САУ? Дайте его графическую интерпретацию?
7. Как представить уравнения движения САУ в форме Коши?
8. Какие методы решения дифференциальных уравнений вам известны?
9. Что называется преобразованием Лапласа? Как оно производится?
10. Какие основные свойства преобразования Лапласа вам известны?
11. Что называется передаточной функций САУ?
12. Как определить изображение сигнала в САУ?
13. Что называется характеристическим уравнением системы?
14. Как определить статические характеристики САУ, если известна ее передаточная функция?
15. Какие методы используются для получения передаточной функции САУ?
16. Для каких начальных условий определяются передаточные функции САУ?
17. Как определяется вектор выходного состояния САУ?
18. Как определить связь между вектором управляющих сигналов и вектором выходного состояния?
19. Для чего используются прямое и обратное преобразования Лапласа?
20. Чем отличаются формы записи дифференциальных уравнений в операторной форме и преобразованных по Лапласу?
21. Что называется структурной схемой САУ?
22. В каких терминах определяется передаточная функция САУ?
23. Для чего проводятся преобразования структурных схем САУ?
24. Как определить передаточную функцию замкнутой САУ относительно любой компоненты вектора ее выходного состояния?
25. Как используются матричные методы для определения передаточных функций САУ?
Тема 5. Типовые динамические звенья
Для анализа САУ используют метод декомпозиции. Для этого система автоматического управления разбивается на динамические звенья.
Динамическим звеном называют устройство любого физического вида и конструктивного оформления, представленное определенным дифференциальным уравнением.
В соответствии с определением классификация динамических звеньев производится по виду дифференциального уравнения, а именно, по его порядку. Так как одними и теми же дифференциальными уравнениями могут описываться устройства любого типа (электрические, электромеханические, гидравлические, тепловые) то такое предположение позволяет использовать для проектирования различных устройств одинаковые подходы.
Динамическое звено можно представить в виде "черного ящика" на который воздействуют управляющее воздействие  и внешнее возмущение
и внешнее возмущение  . Реакция звена на эти воздействия определяется как
. Реакция звена на эти воздействия определяется как 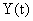 .
.

Рис. 1. Представление динамического звена.
Статическая характеристика любого звена может быть изображена прямой линией, если рассматривается линейная или линеаризованная САУ.
Для звеньев статического типа линейной зависимостью связаны выходная и входная величины в установившемся режиме работы САУ. Коэффициент пропорциональности 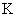 между выходной и входной величинами называется коэффициентом усиления звена.
между выходной и входной величинами называется коэффициентом усиления звена.
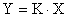 .
.
В звеньях интегрирующего типа линейной зависимостью связаны производная выходной величины и входная величина в установившемся режиме.
 .
.
Для таких звеньев справедливо равенство
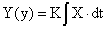 .
.
Коэффициент пропорциональности в этом случае называют добротностью системы.

Рис. 2. Статические характеристики звеньев статического (а) и интегрирующего (б) типа.
5.1. Основные характеристики.
Как отмечалось выше классификация динамических звеньев производится по виду дифференциального уравнения, описывающего поведение звена в динамических режимах работы САУ. Однако вид дифференциального уравнения не является единственным признаком, по которому проводится сравнение динамических звеньев. Для этого используются следующие характеристики:
· Дифференциальные уравнения движения динамического звена.
· Передаточные функции 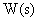 ;
;
· Временные характеристики, к которым относятся:
· переходная функция или переходная характеристика 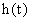 ,
,
· импульсная передаточная функция или функция веса 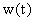 ,
,
· Частотные характеристики, к которым относятся:
· амплитудно-частотные характеристики,
· амлитудно-фазовые частотные характеристики,
· логарифмические частотные характеристики.
Дифференциальные уравнения движения динамического звена, его передаточные функции и частотные характеристики подробно рассмотрены в предыдущих разделах курса.
Временные характеристики
Временные характеристики определяют вид изменения выходного сигнала при подаче на вход звена типового управляющего воздействия. Это позволяет сравнивать свойства звеньев в динамических режимах работы. Временные свойства звена определяются его переходной и импульсной переходной характеристиками.
Переходная функция или переходная характеристика 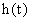 представляет собой переходный процесс на выходе звена, возникающий при подаче на его вход скачкообразного воздействия при величине скачка, равного единице. Такое воздействие называется единичной ступенчатой функцией. и обозначается
представляет собой переходный процесс на выходе звена, возникающий при подаче на его вход скачкообразного воздействия при величине скачка, равного единице. Такое воздействие называется единичной ступенчатой функцией. и обозначается
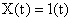 ,
,
что соответствует следующим условиям:
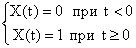 .
.

Рис. 3. Единичная и переходная функции.
Изображение единичной ступенчатой функции определяется как
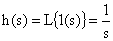 .
.
Чтобы определить изображение переходной функции при известной передаточной функции звена 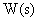 необходимо выполнить следующую операцию:
необходимо выполнить следующую операцию:

Ступенчатая функция представляет собой распространенный вид входного воздействия в САУ. К такому виду воздействия сводятся возрастание момента на валу двигателя, мгновенное изменение задания на частоту вращения двигателя.
Функция веса или импульсная переходная характеристика представляет собой реакцию звена на единичную импульсную функцию. Единичная импульсная функция, или 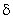 – функция, представляет собой производную от единичной ступенчатой функции. То есть
– функция, представляет собой производную от единичной ступенчатой функции. То есть
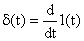 .
.
Дельта-функция тождественно равна нулю во всех точках, кроме 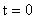 , где она стремится к бесконечности.
, где она стремится к бесконечности.
Основное свойство дельта-функции состоит в том, что
 ,
,
то есть она имеет единичную площадь.
Нетрудно установить, что изображение дельта-функции определяется как
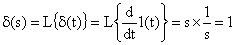 .
.
Изображение функции веса определяется как:
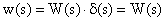
Очевидно, что изображение передаточной функции совпадает с передаточной функцией звена или САУ.
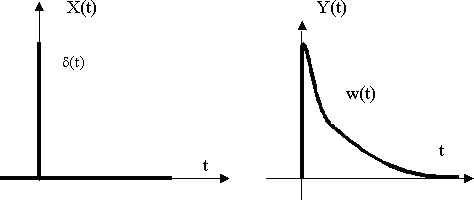
Рис. 4. Дельта-функция и функция веса (импульсная переходная характеристика)
5.2 Основные типовые динамические звенья
Большинство сиcтем может быть представлено совокупностью относительно звеньев с передаточными функциями невысокого порядка. Такие звенья называются типовыми.
Типовым называется такое звено, которое описывается дифференциальным уравнением не выше второго порядка. К таким звеньям относятся:
· безинерционное звено – звено нулевого порядка,
· апериодическое звено – звено первого порядка,
· интегрирующее звено – звено первого порядка,
· дифференциальное звено – звено первого порядка,
· колебательное звено – звено второго порядка.
5.2.1. Безинерционное звено.
Уравнение движения для безинерционного звена имеет вид
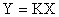 .
.
Выполняя над этим уравнением преобразование Лапласа получаем выражение для передаточной функции звена следующего вида:
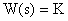
Для нахождения временных характеристик звена определим его реакцию на единичное ступенчатое воздействие. Изображение переходной функции определяется как
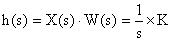 .
.
Выполняя обратное преобразование изображения переходной характеристики 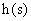 , получаем:
, получаем:

Выполняя аналогичные преобразования над изображением весовой функции, получаем выражение для определения весовой функции 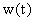 .
.
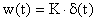
Для построения частотных характеристик звена воспользуемся выражением для его комплексной передаточной функцией вида:
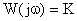
Исходя из этого, амплитудно-частотная характеристика звена представляется точкой на комплексной плоскости.
Логарифмическая частотная характеристика представляется прямой параллельной оси частот. Это следует из выражения для определения логарифмической частотной характеристики вида:
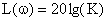 .
.
5.2.2. Апериодическое звено
Уравнение движения для безинерционного звена имеет вид
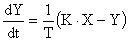 .
.
Выполняя над этим уравнением преобразование Лапласа получаем выражение для передаточной функции звена следующего вида:
Дата добавления: 2015-12-29; просмотров: 1819;
