Пример расчета (задача № 10)
Для схем стальных балок I и II, изображенных на рис. 5.25 и 5.26, определить методом начальных параметров углы поворота сечения и прогиб в точке D. Модуль упругости Е = 2×108 кН/м2. Поперечные сечения балок: схема I - круглое диаметром d = 0,24 м, схема II - квадратное со стороной a = 0,2 м.
Решение
Схема I.
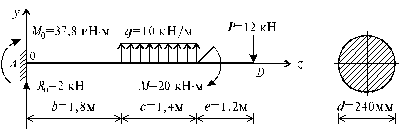
1. Определение опорных реакций балки (рис. 5.25)
Sy = 0, R0 + q×c - P = 0, R0 = -q×c + P = -10×1,4 + 12 = -2 кН;
SM0 =0, 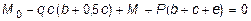 ,
,
M0 = q c (b + 0,5 c) - M - P (b + c + e) = 10×1,4×(1,8 + 0,5×1,4) -
- 20 - 12×(1,8 + 1,4 + 1,2) = -37,8 кН×м.
|
Рис. 5.25
Для проверки правильности определения опорных реакций составим уравнения равновесия:
åMD = 0, M0 + R0×4,4 + q×c×(0,5×c + e) + M = -37,8 - 2×4,4 +
+ 10×1,44×(0,5 1,4 + 1,2) + 20 = 46,6 - 46,6 = 0.
Реакции найдены верно.
2. Применение метода начальных параметров. Используя уравнение (5.23), для нашего случая запишем:
E Ix y (z) = E Ix y0 + 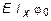 z +
z + 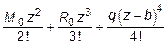
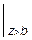 -
-
- 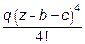
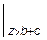 +
+ 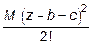
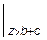 .
.
Здесь M0 и Q0 - момент и реакция в заделке (т.е. в начале координат). Знак ½z > a означает, что слагаемое, после которого он стоит, нужно учитывать при z > a и не надо - при z £ a. Начальные параметры имеют значения: y0 = 0; j0 = 0; M0 = -37,8 кН×м, R0 =
= -2 кН (знак реакций определяется по знаку перемещения вызванного этими усилиями). Тогда выражение для определения прогибов будет иметь вид:
E I y (z) = - 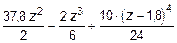
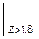 -
- 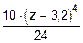
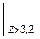 +
+
+ 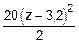
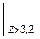 .
.
Соответственно выражение для определения углов поворота будет:
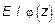 =-37,8×z - z2 +
=-37,8×z - z2 + 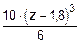
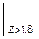 -
- 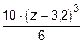
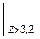 +
+
+ 20×(z - 3,2) 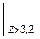 .
.
С помощью этих выражений определяем yD и jD:
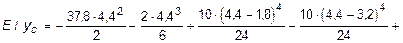
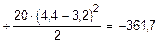 кН×м3.
кН×м3.
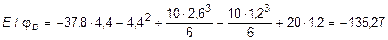 кН×м2.
кН×м2.
Жесткость сечения при Е = 2×108 кН/м2 равна:
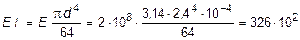 кН×м2.
кН×м2.
Тогда, окончательно:
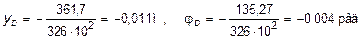
Прогиб точки D происходит вниз, а сечение поворачивается по часовой стрелке.
Схема II.
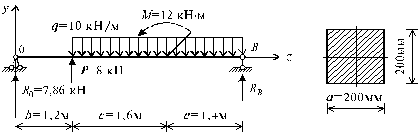
|
Рис. 5.26
1. Определение опорных реакций балки (рис. 5.26).
SM0 =0, RB (b + c + e) - q×(c + e)×[b + 0,5×(c + e)] + M + P b = 0,
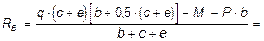
= 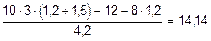 кН;
кН;
SMB =0, R0 (b + c + e) - 0,5×q×(c + e)2 - M + P×(c + e) = 0,
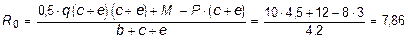 кН.
кН.
Для проверки правильности определения опорных реакций составим уравнение равновесия сил по оси y:
Sy =0; R0 + RB + P - q (c + e) = 7,86 + 14,14 + 8 - 10×3 = 30 - 30 = 0.
Реакции найдены верно.
2. Применение метода начальных параметров. Используя метод начальных параметров, для рассматриваемой балки запишем:
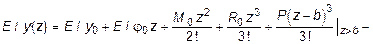
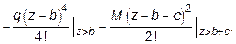
Из условий закрепления балки при z = 0 имеем: y0 = 0; М0=0.
Подставляя числовые значения, получим:
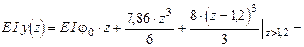
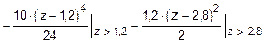 .
.
В данном выражении неизвестно j0. Из условия закрепления балки при z = b + c + e имеем, что y = 0. Вычисляя прогиб на правом конце балки и приравнивая его к нулю, получим уравнение для определения j0:
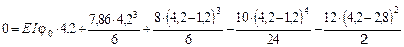 .
.
Отсюда E I j0 = -20,84 кН×м2. Теперь выражение для определения прогибов будет иметь вид:
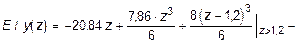
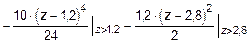 .
.
Соответственно, выражение для определения углов поворота будет:
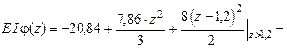
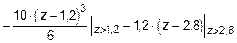 .
.
С помощью этих выражений определяем yD и jD:
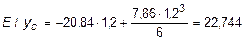 кH×м3.
кH×м3.
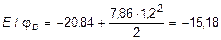 кН×м2.
кН×м2.
Вычисляем жесткость сечения (Е = 2×108 кН/м2):
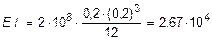 кН×м2.
кН×м2.
Тогда, окончательно,
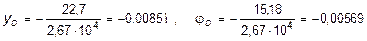 рад.
рад.
Перемещение точки D происходит вниз, а сечение поворачивается по часовой стрелке.
Косой изгиб
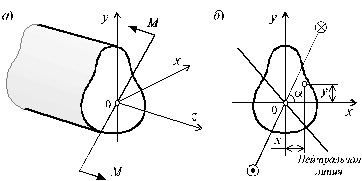
Под косым изгибом понимается такой случай изгиба, при котором плоскость изгибающего момента не совпадает ни с одной из главных осей поперечного сечения (рис. 5.27, а). Косой изгиб удобнее всего рассмотреть как одновременный изгиб бруса относительно главных осей x и y поперечного сечения бруса. Для этого общий вектор изгибающего момента М, действующего в поперечном сечении бруса, раскладывается на составляющие момента относительно этих осей (рис. 5.27, б):
Mx = M×sina; My = M×cosa . (5.25)
Введем следующее правило знаков для моментов Mx и My -
момент считается положительным, если в первой четверти координатной плоскости (там, где координаты x и y обе положительны) он вызывает сжимающие напряжения.
|
Рис. 5.27
На основании принципа независимости действия сил нормальное напряжение в произвольной точке, принадлежащей к поперечному сечению бруса и имеющей координаты x, y, определяется суммой напряжений, обусловленных моментами Mx и My , т.е.
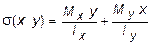 . (5.26)
. (5.26)
Подставляя выражения Mx и My из (5.25) в (5.26), получим:
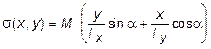 .
.
Из курса аналитической геометрии известно, что последнее выражение представляет собой уравнение плоскости. Следовательно, если в каждой точке сечения отложить по нормали вектор напряжения s, то концы векторов образуют геометрическое место точек, принадлежащих одной плоскости, как и при поперечном изгибе.
Уравнение нейтральной линии, т.е. геометрического места точек, где нормальное напряжение принимает нулевые значения, найдем, полагая в (5.26) s = 0:
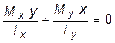 .
.
Откуда определяется:
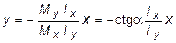 . (5.27)
. (5.27)
Поскольку свободный член в (5.27) равен нулю нейтральнаялиния всегда проходит через начало координат. Как видно из выражения (5.26), эпюра напряжений в поперечных сечениях бруса линейна, следовательно, максимальные напряжения в сечении возникают в точках наиболее удаленных от нейтральной линии. В том случае, когда сечение имеет простую форму (прямоугольник, круг), положение наиболее опасных точек легко определяется визуально. Для сечений, имеющих сложную форму, необходимо применить графический подход.
Далее покажем, что при косом изгибе нейтральная линия не перпендикулярна к плоскости действия изгибающего момента, как это всегда выполнялось при поперечном изгибе. Действительно угловой коэффициент K1 следа момента (рис. 5.27, б) равен:
K1 = tg a . (5.28)
Угловой же коэффициент нейтральной линии, как это следует из (5.27), определяется выражением:
 tg j = K2
tg j = K2 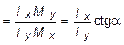 . (5.29)
. (5.29)
Так как в общем случае Ix ¹ Iy, то условие перпендикулярности прямых, известное из аналитической геометрии, не соблюдается, поскольку K1 ¹ 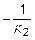 . Брус, образно выражаясь, предпочитает изгибаться не в плоскости изгибающего момента, а в некоторой другой плоскости, где жесткость на изгиб будет минимальной.
. Брус, образно выражаясь, предпочитает изгибаться не в плоскости изгибающего момента, а в некоторой другой плоскости, где жесткость на изгиб будет минимальной.
Дата добавления: 2015-12-29; просмотров: 760;
