Показатели формы распределения

Нормированный момент третьего порядка является показателем асимметрии распределения :

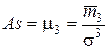. (3.5)

Степень существенности асимметрии характеризуется средней квадратической ошибкой, которая зависит от объема наблюдения:

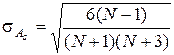, (3.6)

Если 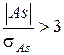, то асимметрия существенна.

При симметричном распределении варианты, равноудаленные от 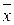, имеют одинаковую частоту, поэтому 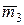= 0, а следовательно, и μ3=0.

Если μ3 < 0, то в вариационном ряду преобладают (имеют большую частоту) варианты, которые меньше 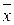, т.е. ряд отрицательно ассиметричен (или с левосторонней скошенностью – более длинная ветвь влево). Положительная асимметрия (правосторонняя скошенность – более длинная ветвь вправо) характеризуется значением μ₃ > 0 (рис. 2.1). В качестве показателя асимметрии применяется и коэффициент асимметрии Пирсона(As):

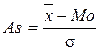. (3.7)

Если As= 0, (т.е. 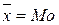), то распределение симметричное (нормальное).

Если As < 0, то имеет место левосторонняя асимметрия.

Если As > 0,то имеет место правосторонняя асимметрия.

Если |As| > 0,25, то асимметрия значительна; если |As| < 0,25 – незначительна.

Рис. 2.1 Асимметрия распределения

Нормированный момент четвертого порядка характеризует крутизну (заостренность) графика распределения:

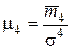. (3.8)

Для нормального распределения μ₄ = 3, поэтому для оценки крутизны исследуемого распределения в сравнении с нормальным из μ₄ вычитается 3 и таким образом рассчитывается показатель эксцесса:

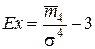. (3.9)

Если Ex = 0, то распределение симметрично;

Ex > 0, то распределение островершинное;

Ex < 0, то распределение плосковершинное (рис. 3.2).

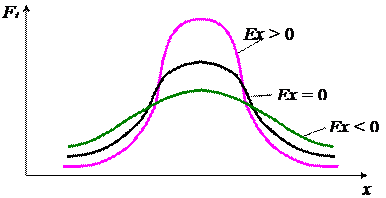Рис. 3.2. Эксцесс распределения