Режимы трения и критерии расчета.

Работа трения является основным показателем работоспособности. В зависимости от режима работы подшипника в нем может быть6 полужидкостное или жидкостное трение. Это все хорошо определено графиком Гарсии-Штрибека.

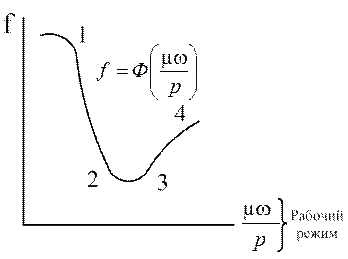
Коэффициент трения очень сильно зависит от количества смазки в зоне контакта. При жидкостном трении рабочие поверхности вала и вкладыша разделены слоем масла, толщина (h>R_z1+R_z2)а. При этом коэффициент трения

находится в пределах 0,001…0,005. При полужидкостном трении условие (а) не соблюдается. При этом наблюдается как жидкостное так и граничное. Граничное называют трение, при котором трущиеся поверхности покрыты тончайшей пленкой смазки. Полужидкостное трение сопровождается износом трущихся поверхностей. Значение коэффициента трения зависит не только от качества масла, но и от материала трущихся поверхностей (0,008…0,01).

Основы теории жидкостного трения

Исследование режима жидкостного трения основано на гидродинамической теории смазки (Н.П. Петров 1883).

При движении пластины А относительно пластины Б со скоростью V_A<V_кр, пластина А выжимает масло из зоны контакта. При этом образуется полужидкостное трение. При скорости V_A>V_кр пластина А поднимается в масляном слое и принимает наклонное положение и между пластинками образуется сужающий зазор, заполненный маслом, а движение происходит в условиях жидкостного трения.

Рассмотрим физику явления, для этого придадим пластинам обратное движение со скоростью V_A, тогда пластина А получит скорость V_A=0, а пластина Б приобретет скорость равную V_A, обратного направления.

Положим далее, что ширина пластины А существенно больше ее длины и в пределе 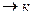. Это позволяет свести задачу к плоской с осями х и у.

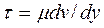= закон Ньютона.

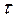- напряжение сдвига от внутреннего трения;

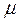- динамическая вязкость жидкости П_а∙с;

v – скорость течения, м/с.

Продифференцировав уравнение Ньютона:

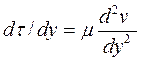
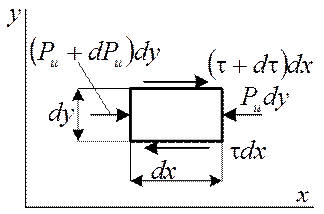
Из условия равновесия получаем:

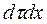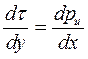dp и dу= или - обозначим

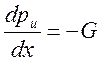- градиент избыточного давления в зазоре.

После подстановки:

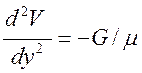
Интегрируя дважды, получим:

V₂=Gу²/(2 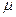+С₁у+С₂

С₁ и С₂ – находим по граничным условиям при у=0 V=V_A при у=h V=0, тогда:

,

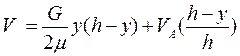h – текущая толщина слоя масла в зазоре.

Объемный расход на единицу ширины равен:

.

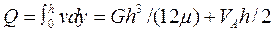По условию неразрывности потока масла Q не должно зависеть от х.

При этом градиент давления G должен изменяться с изменением толщины слоя h:

.

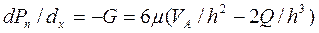Учитывая h=h₁- 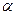x₁ после интегрирования в пределах n₁ до h и граничном условии – при h₁=h p_u=0:

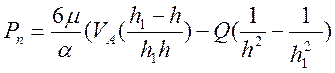
Уравнения Q и P_n можно упростить, имея в виду, что на выходе из пластины, где h=h₂. Избыточное давление P_n=0, тогда:

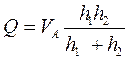
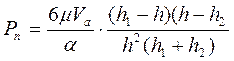уравнение F

Используя полученные решения, можно сделать выводы:

1.Расход жидкости Q одинаков во всех сечениях сужающегося зазора, скорость течения увеличивается справа налево. В то же время на границах с пластинами скорости постоянны и равны скоростям пластин.

2. Давление обратно пропорционально толщине масляного слоя.

В среднем сечении h=(h₁+h₂)/2:

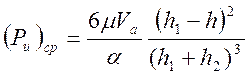
Учитывая малое значение 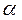, принимаем 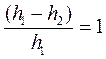и 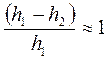, получим: .

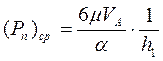3. При стремлении 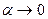и h₁=h = h₂ получим одно из условий образования режима жидкостного трения -этим является сужающийся зазор, который принято называть клиновым.

Рассматривая работу радиального подшипника, обнаруживаем, что клиновая форма зазора свойственна самой конструкции подшипника:

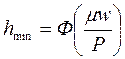
где 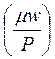- характеристика рабочего режима подшипника.

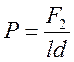- условное среднее давление в подшипнике.

Толщина масляного слоя возрастает с увеличением вязкости масла и угловой скорости цапфы.

С увеличением нагрузки толщина масляного слоя уменьшается.

Для образования режима жидкостного трения необходимы следующие условия:

-между скользящими поверхностями должен быть зазор клиновой формы;

- масло соответствующей вязкости должно непрерывно заполнять зазор;

- скорость относительного движения поверхностей должна быть достаточной, для создания давления, способное уравновесить внешнюю нагрузку.