МАТЕРИАЛЫ, ПРИМЕНЯЕМЫЕ ПРИ КОНСТРУИРОВАНИИ ДЕТАЛЕЙ МАШИН

Выбор материалов при конструировании деталей машин возможен только при полном знании их физико-механических характеристик, технологических свойств и стоимости.

Основными физико-механическими характеристиками являются:

·прочность, характеристиками которой являются предел прочности σ_в; предел текучести σ_т; предел выносливости σ_-1;

·износостойкость, характеризуемая твердостью по Бринеллю – НВ; твердостью по Роквеллу – HRc; твердостью по Виккерсу – HV;

·жесткость, характеризуемая модулем упругости Е первого рода и модулем упругости G второго рода;

·антифрикционность, характеризуемая коэффициентом трения скольжения f;

·коррозионная стойкость, характеризуемая стойкостью материала к коррозии в агрессивных средах;

·другие характеристики, такие как, упругость, коэффициент объемного расширения, теплопроводность, электропроводность и др.

Технологические свойства материала обеспечивают наиболее экономичный способ получения заготовки детали и ее обработки в производственных условиях.

К ним относятся: обрабатываемость резанием; литейные качества, обеспечивающие получение заготовки литьем; обрабатываемость давлением и способность изменять физико-механические характеристики при термической и химико-термической обработке.

При расчете деталей машин на прочность применяют такие регламентированные характеристики материалов, как:

[σ_р] – допустимое напряжение при растяжении;

σ_-1р – предел выносливости при растяжении;

[σ_и] – допустимое напряжение при изгибе;

[σ_см] – допустимое напряжение при смятии;

[τ_ср] – допустимое напряжение на срез;

[τ_кр] – допустимое напряжение при кручении;

Нагрузка, действующая на детали:

I – статическая нагрузка;

II – переменная нагрузка от нуля до максимума (пульсирующая);

III – знакопеременная нагрузка (симметричная).

В справочной литературе твердость материалов часто указывают в разных единицах измерения. В таблице 11.1 дано соотношение между этими единицами.

Таблица 11.1 – соотношение твердостей материалов
и сплавов (ориентировочное)

Допускаемое напряжение при расчете зубьев на изгиб

При нереверсивной нагрузке на горизонтальном участке :

,

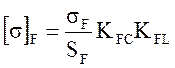где 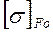- предел выносливости;

S_F – коэффициент (запаса прочности) безопасности, S_F = 1,56…1,75, в среднем 1,7;

К_FC – коэффициент, учитывающий влияние реверсивности…

К_FC = 1 односторонняя нагрузка, К_FC =0,7…0,8 реверс.

К_FL – коэффициент долговечности;

K_FL= 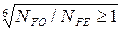, но ≤2→ при →350 НВ;

K_FL= 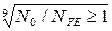, но ≤1,6 при >350 НВ;

N_FO = 4.10⁶ – базовое число для всех сталей.

N_FE = 60 e .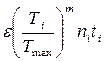

Учет переменности режима работы передачи

Большинство зубчатых передач работает в условиях переменных режимов нагрузок. Расчет этих передач по максимальным нагрузкам привело бы к утяжелению передач. Поэтому расчет ведут по длительно действующей нагрузке, а переменность нагрузки учитывают выбором допускаемого напряжения.

Используя условие суммирования усталостных повреждений 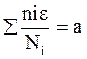и уравнение наклонной ветви кривой усталости (Веллера).

,

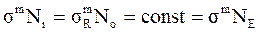где 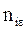- общее число циклов действия некоторого напряжения ;

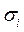N_i – число циклов до разрушения, при том же напряжении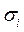

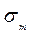- расчетное напряжение;

N_E – эквивалентное число циклов до разрушения;

N_o – число циклов напряжений до перелома кривой усталости, (базовое число циклов).

Умножив и разделив в уравнении суммирования усталостных повреждений на 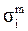получим:

.

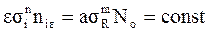Заменим N_o на N_нЕ, тогда 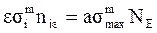, или

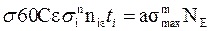, приняв а=1.

Находим 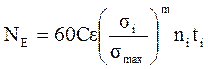, однако расчет по напряжениям не всегда удобен, т.к. требует определения напряжений при каждой нагрузке. Поэтому отношение напряжений, можно заменить отношением моментов:

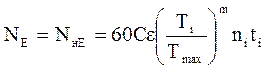_, где m=6…9.

Для расчета по контактным напряжениям:

.

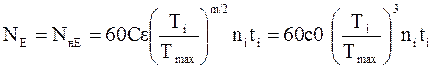Конические передачи.

Конические зубчатые колеса применяют в передачах между валами, оси которых расположены под углом, чаще всего ортогональные передачи с углом 90⁰. Конические передачи изготавливаются с прямыми, тангенциальными и круговыми зубьями. Чаще всего нашли применения конические передачи с круговыми зубьями.

С прямыми зубьями конические передачи применяют при скоростях до 8 м/с.

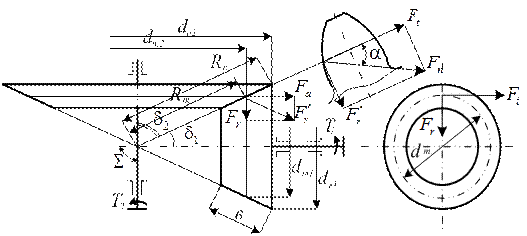
В конических передачах начальные и делительные конуса с углам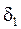и и 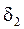являются аналогами начальных и делительных цилиндров цилиндрических передач. Основными параметрами конических передач являются размеры, отнесенные к внешнему торцевому сечению, и обозначаются индексом е.

R_e, d_e и т.д.

В среднем сечении размеры обозначаются с индексом m., R_m, d_m и т.д.

R_e, R_m – внешнее и среднее конусное расстояние;

в – ширина зубчатого венца.

R_e=R_m+0,5в; d_e= d_mR_e/R_m; mt_e=mt_mR_e/R_m

Передаточное число определяется как в цилиндрических передачах:

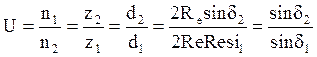
При .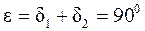

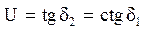Силы в зацеплении (см. рис.) (для шестерни).

F_t=2Т₁/d_m; F_n=F_t/cos 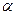; F₂¹=F_ttg 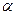х.

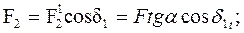
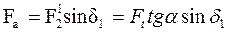
Для колеса:

F_a1=F_r2 и F_r1=F_a2

Приведение прямозубого конического колеса к эквивалентному прямозубому цилиндрическому

Форма зуба конического колеса в нормальном сечении

дополнительным конусом 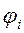такая же, как у цилиндрического прямозубого.

.

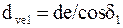
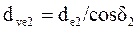Выражая через Z и m, запишем

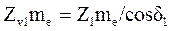или , .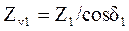

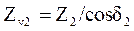Расчет зубьев по контактным напряжениям

;

; ;

.

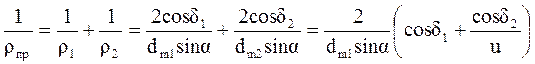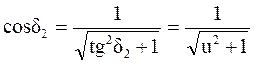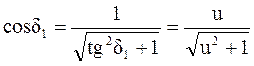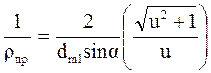Учитывая, что радиус кривизны в различных сечениях зуба пропорционально диаметрам этих сечений или расстоянию от вершины начального конуса. И удельная нагрузка q также пропорциональна этим расстояниям. Следовательно, 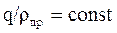для всех сечений.

,

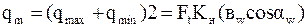
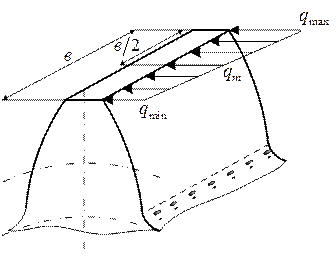
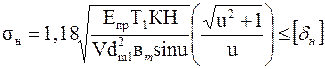где V=0,85 – опытный коэффициент.

Для проектного расчета:

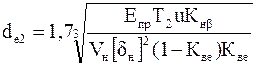, где К_ве=вw/R_e; К_ве≤0,3 (наиболее используемый) (К_ве – 0,285).

Расчет зуба по изгибным напряжениям

При геометрическом подобии зубьев в различных сечениях, их жесткость, как консольных оболочек постоянна по всей ширине колеса. Для оценки деформации положим, что зубья колеса 2 абсолютны жесткие, а зубья колеса 1 податливые. При заторможенном колесе 2 нагруженное колесо 1 повернется на угол 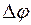. Прогиб в различных сечениях равен 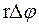. При постоянной жесткости нагрузка пропорциональна деформациям. Или радиусам r, которые, в свою очередь, пропорциональны расстояниям от вершины делительного конуса. При этом напряжения изгиба постоянны по длине зуба:

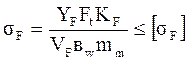
V_F= 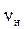=0,85.

Червячные передачи

Передача, сочетающая в себе два типа передач – винтовую и зубчатую. Поэтому движение в червячной передаче преобразуется по принципу винтовой пары или наклонной плоскости.

Геометрические параметры и способы изготовления передач.

В червячных передачах, как и в зубчатых различают:

d_w1, d_w2 - начальные диаметры ш и к

d₁, d₂ - делительные диаметры ш и к.

Червяки: Различают по следующим признакам: форме поверхности – цилиндрические и глобоидные; по форме профиля – с прямолинейным и криволинейным профилем в осевом сечении.

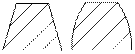
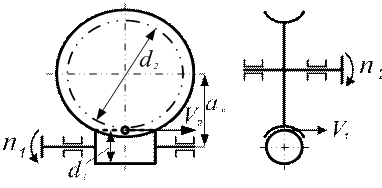
По стандарту Z₁=1, 2, 4. Обычно рекомендуют Z₁ =4 при t=8…15, Z₁=2 при i=15-30; Z₁=1 при i≥30. Делительны2й диаметр червяка связан с модулем q=d₁/m

m=2,25; 315; 4; 5; 6,3; 8; 10;12,5.

q= 8; 10; 12,5; 16; 20.

Для предотвращения сильного прогиба червяка: q≥0,25Z₂

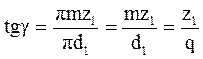
При этом:

d₁=qm; d_a1=d₁+2m; df₁=d₁-2,4m;

Длина нарезаемой части червяка

При х=0

в₁≥(11+0,06Z₂)m →при Z₁-=2

в₁≥(12,5+0,09Z₂)m →при Z₁-=4

Колеса:

d₂=Z₂m, d_a2=d₂+2m; df₂=d₂-2,4m; a_w=0,5(q+Z₂)m;

По условию не подрезания зубьев Z₂≥28. При 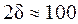z₁=1

d_aМ₂ ≤ d_a2+2_m; ≤d_a2+1,5m; ≤d_a2+m

в₂ ≤0,75d_a1 ≤0,67d_a1

Кинематические параметры передач

Передаточное отношение

В червячной передаче, в отличие от зубчатой, окружные скорости V₁ и V₂ не совпадают, т.е. находятся в ┴ плоскостях. В относительном движении начальные цилиндры не обкатываются, а скользят. Поэтому:

i=n₁/n₂= z₂/z₁

В силовых передачах i=10…60(80), в кинематических цепях приборов i до300. Ведущим в большинстве случаев является червяк.

Скольжение в зацеплении:

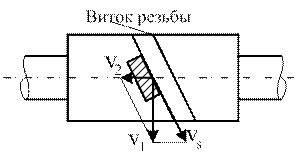
При движении витки червяка скользят по зубьям колеса, как в винтовой паре. Скорость скольжения V_s направлена по касательной к винтовой линии червяка.

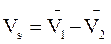или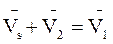

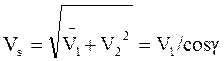
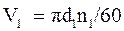
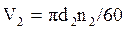
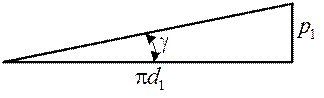
V₂/V₁=tg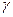

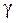- угол подъема винтов линии червяка.

Практически 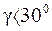, поэтому V₂<<V₁ и V_s>V₁

КПД червячной передачи

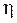зацепления = .

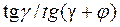КПД увеличивается с увеличением числа заходов червяка при 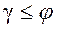; 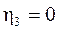передача движения от колеса к червяку становится невозможной. Получаем самотормозящую пару. КПД такой передачи <0,5. Для надежности самоторможения рекомендуют .

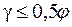Силы в зацеплении.

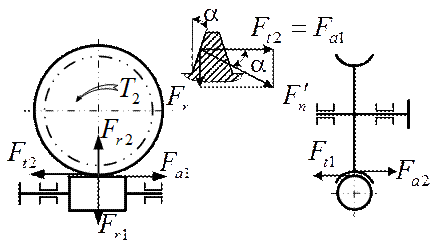
F_t1=F_a2=2Т₁/d₁

F_t2=F_a1=2Т₂/d₂

F_r=F_t2tg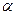

F_n=F_t2 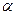/(cos cos )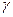

F_n¹=F_ncos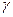

Т₂=Т₁i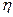

Расчет на прочность

Основные критерии работоспособности и расчета.

1. Повышенный износ и заедание связаны с большими V_s и неблагоприятным направлением скольжения относительно линии контакта – применяется антифрикционные пары материалов. Сталь –бронза (чугун).

2. Устранение заедания не устраняет абразивный износ. Интенсивность износа зависит от значения 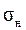. Поэтому расчет по условию 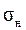≤ 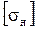являются основным.

Расчет на прочность:

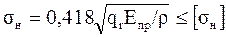
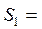для архимедовых червяков

.

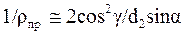По аналогии с косозубыми передачами:

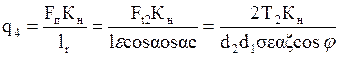
где 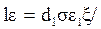- суммарная длина контактных линий. E 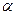=1,8…2,2 торцевой коэффициент перекрытия; 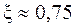- коэффициент, учитывающий уменьшение длины контактных линий в связи с тем, что соприкосновения осуществляется не по полной дуге охвата ( 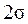). После подстановки:

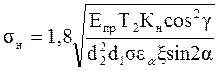
при 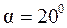и х=0

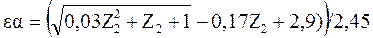
Для проектного расчета:

,

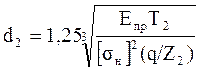где d₁=qm=qd₂/Z₂; 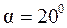; K_н=1,1; ;

; ,

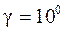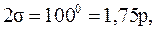
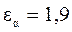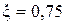Учитывая а_w=0,5d₂(q/Z₂+1), тогда:

.

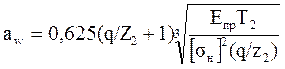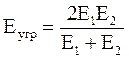; Е₁=2,1∙10⁵МПа - сталь

Е₂=0,9∙10⁵МПа – чугун, бронза.

При проектных расчетах, для силовых передач:

q/Z₂=0,22…0,4

Расчет на прочность по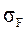

Точный расчет напряжения изгиба усложняется переменной формой сечения зуба по ширине колеса и тем, что основание зуба расположено не по прямой линии, а по дуге окружности.

В приближенных расчетах червячное колесо рассматривают как косозубое. При этом в формулу 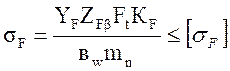введем следующие поправки и упрощения.

1. По своей форме зуб червячного колеса прочнее зуба косозубого колеса (40%). Особенности формы зуба червячных колес учитывает коэффициент формы зуба Y_F.

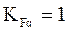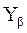2. Червячная пара сравнительно хорошо прирабатывается. Поэтому и =1.

,

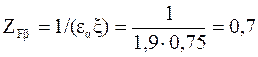Тогда:

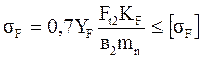
m_n=mcos 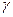, коэффициент Y_F определяем в зависимости от Z_v=Z₂/cos³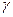

K_F=K_vK ;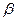

K_v – коэффициент динамики

K 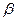; - коэффициент концентрации нагрузки.

При достаточной точности изготовления принимают:

K_v≡ 1 при v≤3 м/с

K_v≡ 1…1,3 при v>3 м/с.

При постоянной нагрузке K 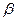≈1; при переменной K 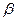=1,05…1,2 – большие значения при малых q и больших Z₂.

Материалы и допускаемые напряжения

В связи с высокими скоростями скольжения и неблагоприятными условиями смазки, материалы червячной пары должны обладать антифрикционными свойствами.

Червяки: изготавливаются из углеродистых и легированных сталей. Подвергаются Т.О. до высокой твердости.

Червячные колеса: изготавливаются из бронзы, реже из латуни и чугуна. Бронзы типа ОФ 10-1, ОНФ считаются лучшими материалами для червячного зацепления, но они дорогие. Применяются при V₃=5…25 м/с. Безоловянистые бронзы типа АЖД-4 обладают повышенными механическими свойствами (НВ, 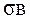), но имеют пониженные противоударные свойства. Их применяют в паре с червяками HRC>45 при V_s≤5м/с. Чугун серый или модифицированный применяют при V_s≤2м/с преимуществнно в ручных приводах.

Допускаемые контрактные напряжения.

Оловянистые бронзы 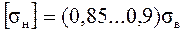при шлифованном и полированном червяке HRC>45.

Если условия не соблюдены, то .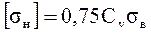

Для бронзы 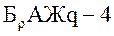→ 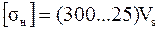при шлифованом и полированном червяке с HRС_c≥45; С_v – коэффициентом, учитывающим скорость скольжения.

При проектных расчетах V_s=4,5∙10^-4 .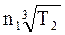

Допускаемые напряжения изгиба.

Для всех марок бронз:

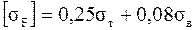
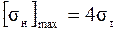→ оловянистые бронзы

.

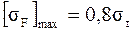Бронза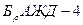

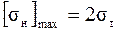
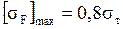
Тепловой расчет, охлаждение и смазка

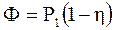t₀=20 ⁰C

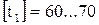
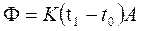
K 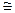14…17(Вт/м^{2 0}С → с применением вентиляции помещения.

K 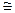8…10(Вт/м^{2 0}С → без вентиляции помещения.

Икусственное охлаждение

K 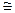20…28(Вт/м²) ⁰С → вентилятор

K 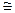до…200(Вт/м²) ⁰С → охлаждение водой

Тепловой расчет червячной передачи

Без вентиляции

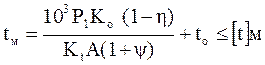
К_о – коэффициент режима К_о<1,0;

К_t – коэффициент теплопередачи корпуса;

А – площадь охлаждения А≈ 20 a_w; 1,7

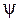- коэффициент теплоотвода, 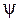=0,25…0,3

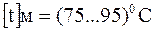
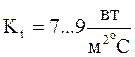- плохая циркуляция воздуха

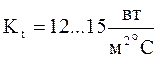- интенсивная циркуляция.

Вентилятор

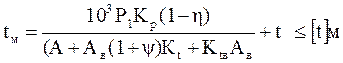
А_в 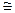6_аw 1,7.

Из расчета на нагрев выполняется проверка

Без охлаждения:

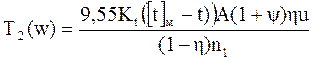
С охлаждением:

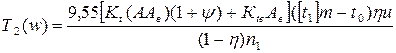
Расчет червяка на жесткость

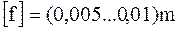
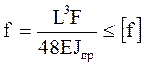
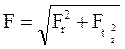
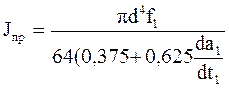
РЕМЕННЫЕ ПЕРЕДАЧИ

Принцип действия и классификация

Передача состоит из двух шкивов, закрепленных на валах и ремня, охватывающего шкивы.

Нагрузка передается силами трения, возникающие между шкивами и ремнем вследствие натяжения последнего.

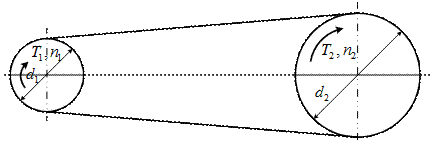
В зависимости от формы поперечного сечения ремня различают: клиноременную, плоскоременную, круглоременную (с) передачи:

По сравнению с другими типами передач ременная обладает рядом особенностей:

1. Возможность передачи движения на значительное расстояние (до 15 м и более);

2. Плавность и бесшумность работы.

3. Предохранение механизмов от резких колебаний нагрузки, предохранение от перегрузки.

4. Простота конструкции и эксплуатации.

Основными недостатками являются:

1. Повышенные габариты.

2. Некоторое непостоянство передаточного числа.

3. Повышенная нагрузка на валы и опоры, из-за большого предварительного натяжения ремня (в 2-3 раза)

4. Низкая долговечность ремней (от 1000 до 5000).

Ременные передачи применяют преимущественно в тех случаях, когда по условиям конструкции валы расположены на значительном расстоянии. Мощность современных ременных передач не превышает 50 кВт.

Основы расчета ременных передач

Теоретические основы расчета являются общими для всех типов ремней.

Критерий работоспособности и расчета. Основными критериями работоспособности передач являются: тяговая способность, определяемая силой трения между ремнем и шкивом – долговечность ремня.

В настоящее время основным расчетом является расчет на тяговую способность.

Кинематические параметры:

Окружные скорости:

.

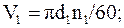
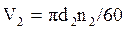Учитывая упругое скольжение ремня:

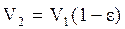, тогда

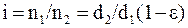, где 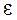- коэффициент скольжения

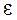≈0,01…0,02 – при нормальных рабочих нагрузках.

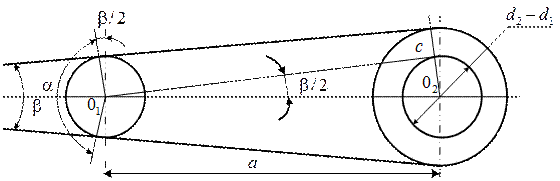
Геометрия передачи:

Основными геометрическими параметрами являются:

а – межосевое расстояние;

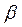- угол между ветвями ремня;

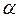- угол обхвата ремнем малого шкива;

d₁ , d₂ – диаметры ведущего и ведомого шкивов.

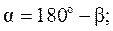
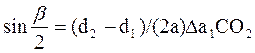
т.к. 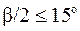, то 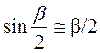, тогда:

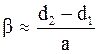или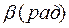

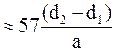
При этом:

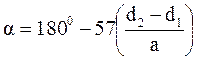, или

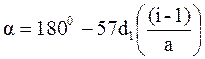
Длина ремня будет:

.

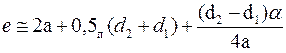При заданной длине ремня:

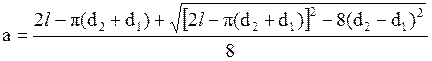
Силы и силовые зависимости.

Рассмотрим нагружение ремня, когда Т₁=О и Т>О

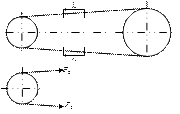
Окружная сила будет 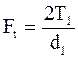и из условия равновесия шкива:

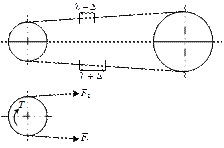
Т₁=0,5d₁(F₁-F₂) или = F₁-F₂=F_t(a).

Геометрическая длина ремня не зависит от нагрузки и дополнительная вытяжка ведущей ветви, компенсируется равным сокращением ведомой ветви.

F₁=F_о +∆F; F₂= F_о -∆F или F₁+F₂=2F_o(в).

Учитывая (а) и (в), получим:

F₁=F_o+F_t/2 и F₂=F_o-_t/2

Получив данную систему уравнений, замечаем, что они не определяют тяговую способность передачи, а лишь устанавливают изменения натяжений ведущей и ведомой ветви от силы F_t. Впервые такая связь была установлена Эйлером. Рассмотрим элемент ремня под действующим нагрузкам в равновесии:

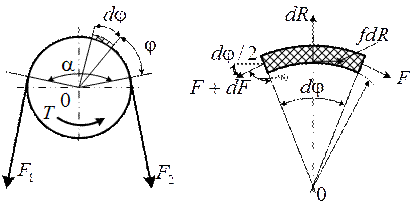
По условию равновесия

а сумма моментов:

0,5dF+0,5dfR-0,5d(F+dF)=0,

fdR=dF(c).

б) сумма проекций относительно «У»

.

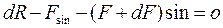Принимая 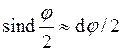и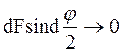

Получим:

dR=F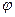d (d).

Решая совместно уравнения (с) и (d)

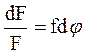, проинтегрируем

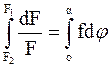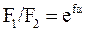; или

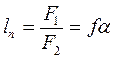
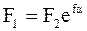(е)

Решая совместно уравнения (а) и (е) с учетом (в), находим:

/

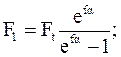
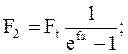
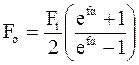При работе ременной передачи, ремень движется со скоростью v= 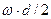и обладая массой m, вызывает появление центробежных сил. Из условия равновесия ремня, под действием этих сил находим:

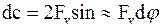и сама сила:

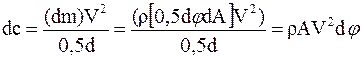
Решая совместно 2 уравнения, находим:

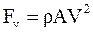
Влияние центробежных сил существенно только при больших скоростях v>20 м/с

Напряжения в ремне

Наибольшие напряжения в ремне возникают в ведущей ветви:

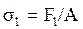
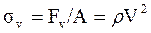
Учитывая ранее полученные зависимости между силами в ремне:

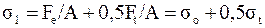, где

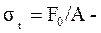полезное напряжение.

При обегании шкива ремень испытывает напряжения изгиба, согласно закона ГУКА:

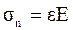, где 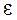- относительное удлинение наружных волокон - 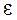=У/r.

У – расстояние от нейтрального слоя;

R – радиус изгиба нейтрального слоя.

,

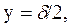
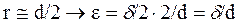
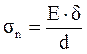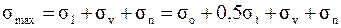
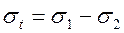
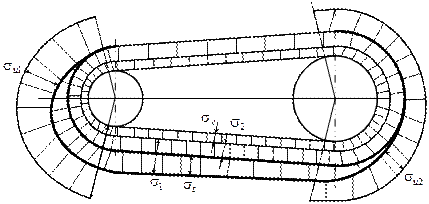
Влияние отдельных составляющих суммарного напряжения на тяговую способность и долговечность ремня

Тяговая способность передачи характеризуется значением максимально допустимой окружной силы F_t или :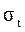

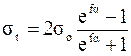
Согласно зависимости по условию отсутствования буксования 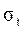возрастает с увеличением 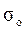. Однако практика показывает снижение долговечности ремня с увеличением .

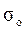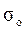МПа 0,9 0,1 1,2 1,5 1,8

отн. долг % 420 250 100 33 13

Поэтому рекомендуют:

Для клиновых ремней 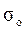≤1,5 МПа

Для плоских ремней 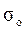≤1,8 МПа

При указанных значениях 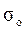допустимое значение 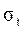≤ 2,0…2,5 МПа.

Оценивая влияние центробежных сил получим (принимая среднее значение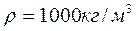

Тогда:

V=10м/с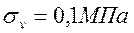

V=20м/с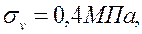

V=40м/с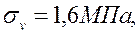

Влияние центробежных сил не велико, особенно для передач, используемых на практике:

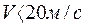и

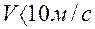
Оценивая влияние напряжений изгиба при Е=200МПа:

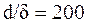
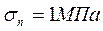
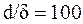
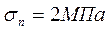
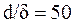
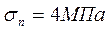
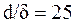
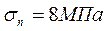
Напряжения изгиба наибольшие из всех видов напряжений.

В отличие от 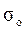и 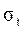увеличение 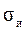не способствует повышению тяговой способности передачи. Более того, 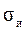как периодически изменяющиеся являются главной причиной усталостного разрушения ремней.

Долговечность ремня зависит и от частоты цикла изменения напряжений.

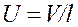
Для плоских ремней U≤3…5 c^-1

Клиновых U≤10…20 c^-1

Скольжение в передаче

Упругое скольжение + буксование

Кривые скольжение и КПД.

Работоспособность ременной передачи принято характеризовать кривыми скольжения и КПД. При построении экспериментальных кривых скольжения и КПД, нагрузочную способность передачи оценивают через коэффициент тяги.

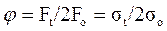
Коэффициент тяги 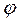позволяет судить о том, какая часть усилия F_o, используется полезно для передачи нагрузки F_t, т.е. характеризует степень загруженности передачи.

Допускаемые полезные 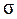в ремне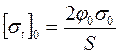

S≈1,2…1,4 – запас тяговой способности по буксованию.

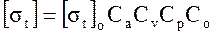
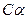- коэффициент угла охвата;

С_v - скоростной коэффициент;

С_р – коэффициент режима нагрузки;

С_о – коэффициент, учитывающий способ натяжения ремня и наклон к горизонту.

Способы натяжения ремней

Нагрузка на валы

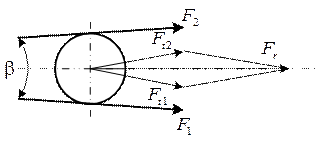
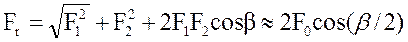
F>(2…3)F_t→ это недостаток ременной передачи у зубчатых F_r≡F_t

Цепные передачи

Общие сведения

Принцип действия цепной передачи основан на зацеплении цепи и звездочек, что повышает прочность стальной цепи по сравнению с ремнем. Отсутствие трения и буксования обеспечивает постоянство передаточного отношения и возможность работы при значительных кратковременных перегрузках. Цепные передачи имеют и недостатки. Основная причина заключается в том, что цепь состоит из отдельных звеньев и располагаются на звездочке по многоугольнику. Это приводит к износу шарниров цепи, шуму и дополнительным динамическим нагрузкам.

Область применения → с/х машиностроение, транспортное, станкостроительное, химическое и т.д.

Основные характеристики

Мощность → Р=VF_t до 100 кВт. Скорость и частота вращения → 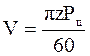применяются при v до 15 м/с и n до 500 мин^-1. Передаточное отношение → 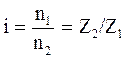, наиболее распространены I до 6(10). КПД → среднее значение 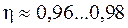межосевое расстояние и длина цепи 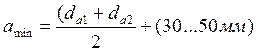. По соображениям долговечности цепи на практике рекомендуют: а=(30…50) Р_ц

30Р_ц при i 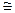1..2. 50 Р_ц при i=6…7

Длина цепи, выраженная в шагах или числом звеньев цепи.

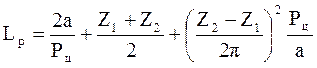
Уточненное значение а при принятом L_р:

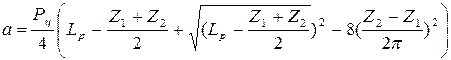
Передача работает лучше при небольшом провисании цепи, поэтому:

а_р=а-(0,002…0,004)а.

Конструкция основных элементов

Приводные цепи

Основная характеристика цепи: шаг, ширина и разрушающая нагрузка.

Роликовая цепь – однорядная, двухрядная 3х и 4х. Применяются при V до 20 м/с.

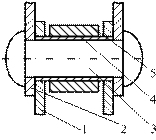
1 – внутреннее звено цепи;

2 – внешнее звено цепи;

3 – валик, запресованный в звено 2;

4- втулка, запрессованная в звено 1;

5 – ролик.

Втулочные цепи – по конструкции такие же, но отсутствует ролик.

Зубчатые цепи – применяют при v до 35 м/с.

Звездочки приводных цепей )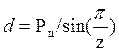

Материалы→стали 45, 40Х, пластины →стали 45,50 для валиков и роликов – стали 15, 20, 20Х.

Силы в цепной передаче

Силовая схема цепной передачи аналогична силовой схеме ременной передачи.

F₁-F₂=F_t; F_v=qv², Fo=K_faqg

K_f – коэффициент провисания;

а – длина свободной ветки цепи;

g – масса единицы длины цепи;

q – ускорение свободного падения (силы тяжести).

При стреле провисания f= (0,01…0,02)а принимают:

K_f =6 – при горизонтальном расположении передачи

K_f =3 – при угле положения 40⁰

K_f =1 – при угле положения 90⁰

На практике для передач при v≤10 м/с

F_v~0,1% F₀~4% от F_t, поэтому для практических расчетов можно принять

F₁≈F_t, F₂≈O

Кинематика и динамика цепной передачи

Неравномерность движения и колебания цепи:

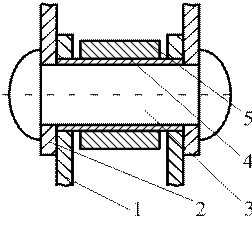
V₂=V_cos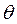

V₁=V_sin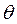

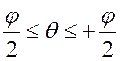
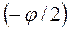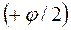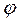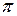Угол соответствует моменту входа в зацепление шарнира А₁ угол - шарнираВ, а = 2 /Z.

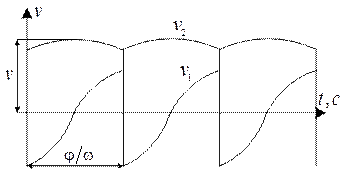
Движение ведомой звездочки определяется скоростью V_2. Периодическое изменение этой скорости сопровождается непостоянством i и дополнительными динамическими нагрузками.

Со скоростью V₁ связаны поперечные колебания цепи и удары шарниров цепи о зубья. Эти отрицательные свойства цепной передачи проявляются тем больше, чем меньше число зубьев звездочки Z.

Изменения i≤1…2%, а динамические нагрузки несколько процентов от F_t.

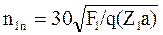
F₁ - натяжение ведущей ветви;

q – масса 1 м длины цепи.

Удар шарнира о зуб и ограничение шага цепи

В момент входа шарнира цепи в зацепление вертикальные составляющие скорости V₁ и V₁¹ направлены навстречу друг-другу – соприкосновение шарнира с зубом сопровождается ударом.

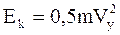, здесь 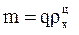- масса цепи;

V_у – скорость удара.

.

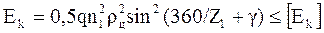Критерии работоспособности и расчета

Основной причиной потери работоспособности является износ шарниров цепи.

.

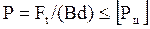Износ шарниров и его связь а параметрами передачи

При работе цепного привода в шарнирах совершаются повороты на угол 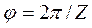, за один пробег цепи совершается четыре поворота - два на ведущей и два на ведомой звездочки. Эти повороты и вызывают износ втулок и валиков.

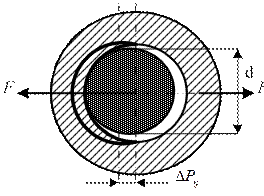
Срок службы цепи по износу зависит от а, числа зубьев Z₁, нагрузки или давления Р, условия смазки, 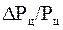- относительный износ.

Решающее значение оказывает на долговечность давление Р в шарнирах. Опытами установлено, что влияние это проявляется в степенной форме и значительно превышает влияние всех остальных факторов.

Допускаемое значение износа и рекомендации по выбору Z

Допускаемое значение относительного износа 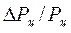ограничивается возможностью потери зацепления со звездочкой, а также уменьшение прочности цепи. При износе меняется шаг цепи.

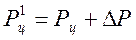
При этом изношенная цепь с увеличенным шагом располагается на новом диаметре звездочки:

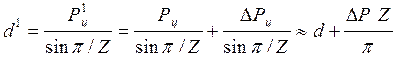
Нетрудно заметить, что зацепление возможно при условии:

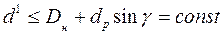
где D_н – наружный диаметр звездочки;

d_р – диаметр ролика

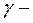угол контакта.

Согласно формуле, видно, что при износе ∆Р_ц и диаметр d¹ возрастает с увеличением Z_1. Это влечет спадание цепи со звездочки. По условию сокращения зацепления выгодно применять звездочки с малым Z. Таким образом, при выборе Z встречаются 2 противоречия.

С одной стороны, при большом Z цепь изнашивается медленнее, но зато мало изношенная, далеко не потерявшая прочности цепь теряет зацепление со звездочкой.

С другой стороны – при малом числе зубьев цепи изнашиваются быстрее, но зато и при большом износе цепь не теряет способности зацепления со звездочкой. Поэтому на основе опыта рекомендуют Z₁ :

i= 1…2 2…3 3…4 4…5 5…6 > 6

Z₁ = 30…27 27…25 25….23 23…21 21….17 17….15

Допускаемое давление в шарнирах цепи

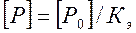
К_э=К_ДК_аК_нК_регК_сК_реж,

К_р – коэффициент динамической нагрузки;

К_а – коэффициент межосевого расстояния или длины цепи;

К_н – коэффициент наклона передачи к горизонту;

К_рез – коэффициент способа регулирования;

К_с – коэффициент смазки и загрязнения передачи;

К_реж - коэффициент режима работы.