Свободное истечение
Свободное истечение (см. рис. 9.22) наблюдается в следующих случаях:
· поток в нижнем бьефе находится в бурном состоянии: i0>iкр, hн<hкр;
· поток в нижнем бьефе в спокойном состоянии. Поток жидкости, вытекающий из-под щита, будет сопрягаться в виде отогнанного прыжка или прыжка в сжатом сечении.
При открытии щита на высоту а от дна русла поток, вытекающий из-под щита, обтекая нижнюю часть его, сужается по вертикали. В результате этого происходит сжатие потока. В сжатом сечении глубина потока равна hс (см. рис. 9.22).
Глубину потока в сжатом сечении можно выразить через высоту открытия щита а и коэффициент сжатия потока 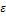 :
:
hc= 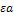 . (9.52)
. (9.52)
Коэффициент вертикального сжатия зависит от открытия щита а и геометрического напора перед щитом H, ε = f  .
.
Для определения свободного истечения определяется глубина hc", сопряженная с глубиной в сжатом сечении. Свободное истечение будет иметь место, когда hc"> hн (hн — глубина воды в нижнем бьефе).
Свободное истечение из-под щита подобно истечению потоков через водосливы с широким порогом.
Расход потока при свободном истечении из-под щита выражается уравнением расхода, как для водослива с широким порогом:
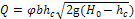 (9.53)
(9.53)
где φ — коэффициент скорости; b — ширина русла, где установлен щит;
H0 — полный напор потока перед щитом.
Уравнение (9.53) с учетом (9.52) можно записать в виде
Q=φab 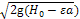 . (9.54)
. (9.54)
Значения коэффициента скорости φ при истечении из-под плоского щита можно принять следующими:
· отверстие без порога — φ = 0,95 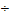 0,97 (см. рис. 9.22);
0,97 (см. рис. 9.22);
· отверстие с широким порогом — φ =0,85 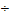 0,95.
0,95.
Для определения расхода потока при свободном истечении из-под щита используется следующая формула:
Q=φ 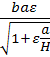
 . (9.55)
. (9.55)
Значения функции φ = f(Fr) по А. Альтшулю приведены в V2 табл. 9.5 (число Фруда Fr =  ).
).
Таблица 9.5 Значения функции <р = f (Fr)
Fr = 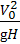
| 0,01 | 0,025 | 0,06 | 0,1 и более | |
| φ | 1,06 | 1,0 | 0,97 | 0,96 | 0,96 |
Для плоского вертикального щита А. Альтшуль рекомендовал при определении коэффициента сжатия формулу
ε=0,57+ 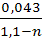 , (9.56)
, (9.56)
где n =  .
.
Расстояние от плоскости отверстия щита до сжатого сечения на основании экспериментов l  0,75а.
0,75а.
Длина прыжка lп вычисляется по формулам, приведенным в гл. 8.
Дата добавления: 2015-12-29; просмотров: 1072;
