Истечение газов через суживающиеся сопла

Начало отсчёта скорости в соплах (во входном сечении) принято ω=0. Уравнение первого закона термодинамики 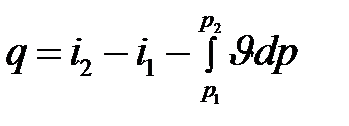при адиабатном истечении рабочего тела через сопло:

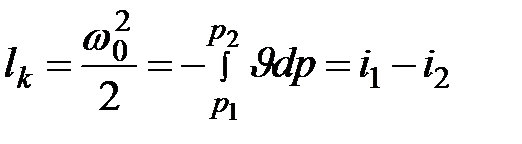
где ω₀ – теоретическая скорость, потока в выходном сечении сопла;

p₁ – начальное давление рабочего тела;

р₂ – давление среды, в которую, происходит истечение.

Исходя из равенства 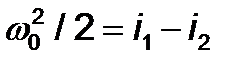, теоретическую скорость истечения рабочего тела через сопло в рассматриваемом случае можно определить:

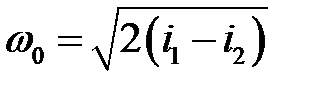
Для идеальных газов формула теоретической скорости истечения получается след. образом:

,

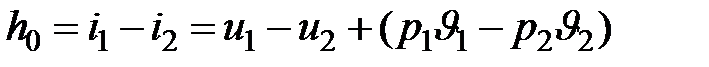а поскольку в адиабатном процессе ,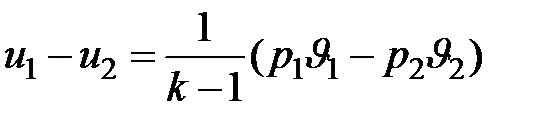

получаем .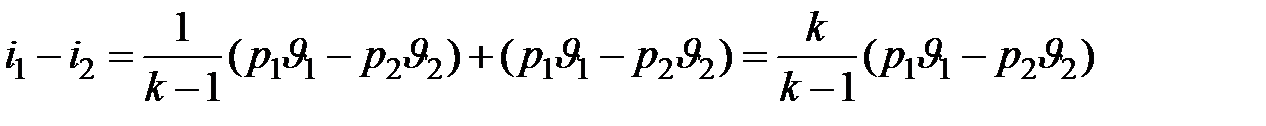

Тогда .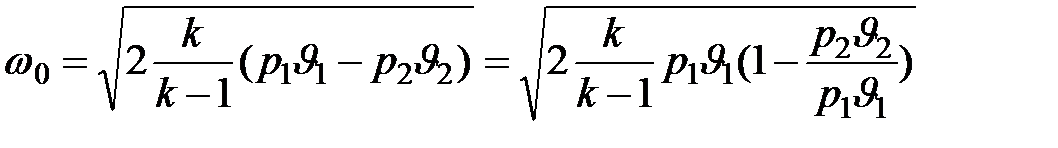

Основной характеристикой процесса истечения является отношение конечного давления к начальному .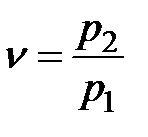

Выразим теоретическую скорость истечения ω₀ как функцию величины ν:

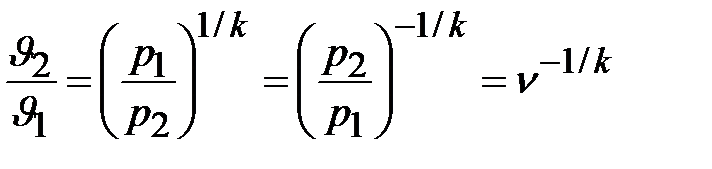и .

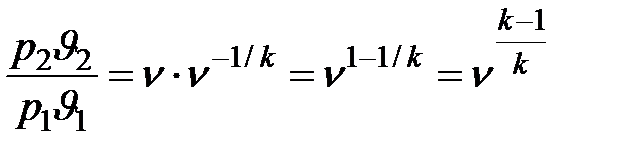Тогда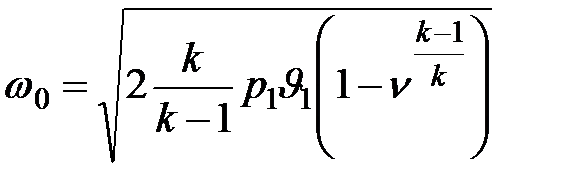

Обозначив площадь выходного сечения канала через f₂, в соответствии с формулой неразрывности потока G₂=ρ₂ω₀f₂:

Преобразуя ,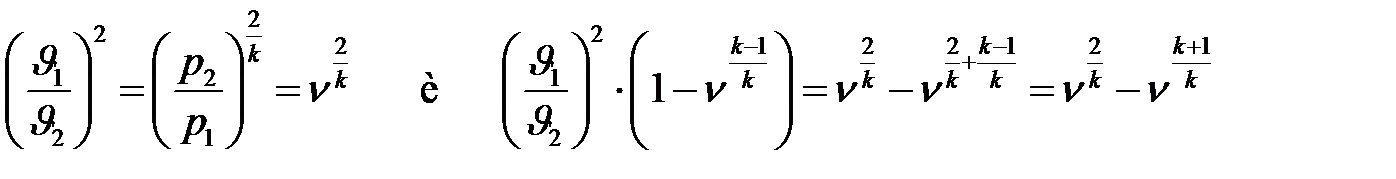

имеем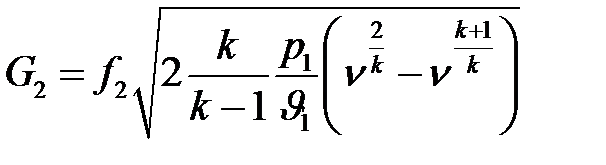

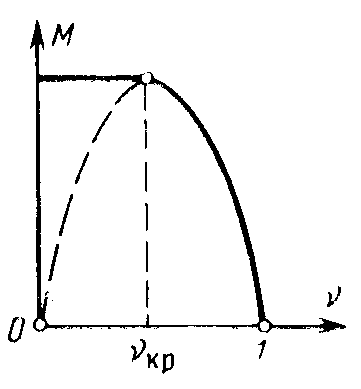
Анализ данного выражения показывает, что при 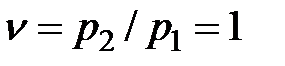, т.е. когда р₂ = р₁, расход газа G₂ = 0, т.е. истечение газа не происходит. При уменьшении ν расход газа возрастает, но при ν = 0 он опять становится нулевым.

Из сказанного вытекает, что при некотором значении 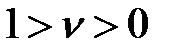расход газа G₂ достигает максимума.

Чтобы найти значение ν, соответствующее максимуму G₂, следует приравнять нулю первую производную функции ,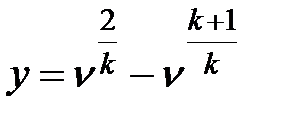

Т.е.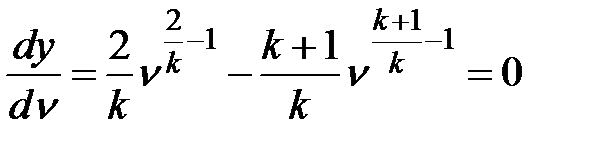

После преобразований получим .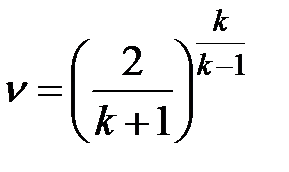

Значение ν, при котором расход газа достигает максимума, называется критическим ν_кр:

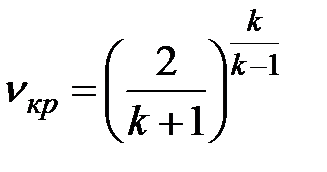
Как и показатель адиабаты, величина ν_кр является физической константой газа.

В действительности после достижения максимума расход газа с уменьшением ν не уменьшается, а остается постоянным.

При уменьшении давления газа за соплом р₂ (при неизменном давлении p₁) расход газа увеличивается, а затем, когда за соплом устанавливается критическое давление 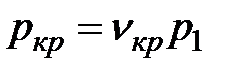, увеличение расхода газа прекращается и, как бы ни уменьшалось давление р₂, в выходном сечении будет иметь место постоянное давление р_кр.

Расширение газа будет происходить уже вне сопла и потому не даcт дополнительного возрастания скорости.

Значение критической скорости:

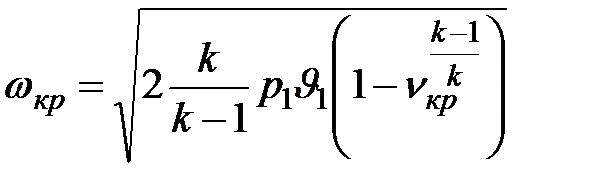
Подставляя сюда 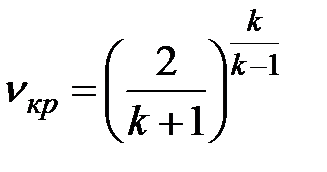и выполнив преобразования, получим:

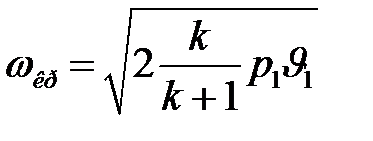
Найдем зависимость между величиной ω_кр и параметрами газа

в выходном сечении р_кр и υ_кр.

При адиабатном истечении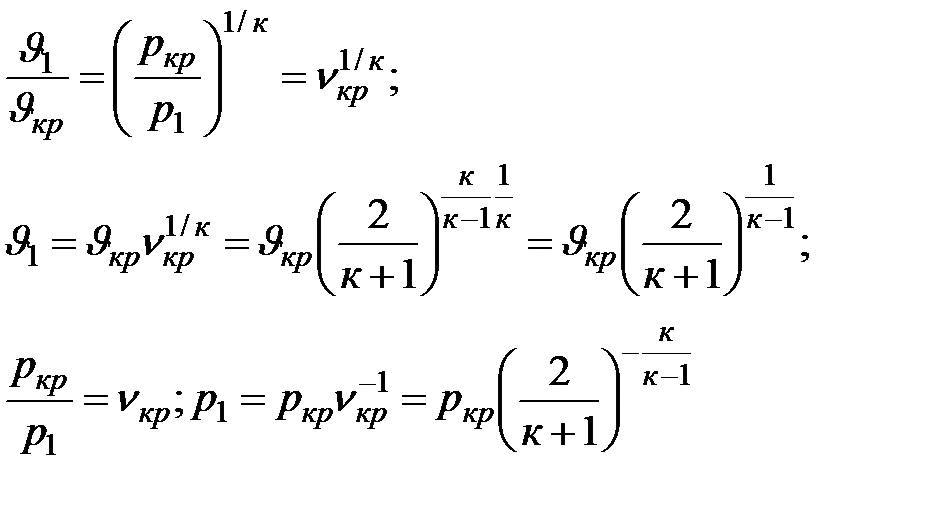

Тогда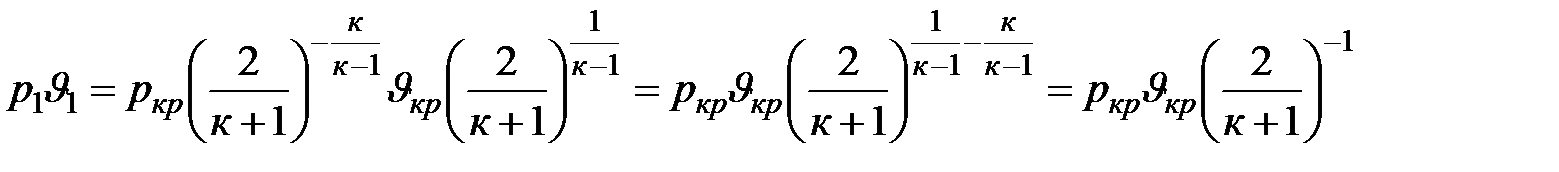

В итоге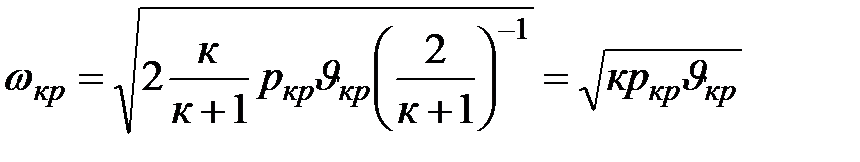

Из физики известно, что скорость распространения звука в газовой среде выражается формулой .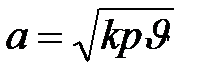

Т.о. критическая скорость истечения газа из сопла равна скорости распространения звуковой волны в этом газе при его параметрах р_кр и υ_кр.

В этом содержится физическое объяснение тому, что при снижении внешнего давления р₂ ниже р_кр, скорость истечения не изменяется, а остается равной ω_кр.

Действительно, если р₂ > р_кр, то ω < ω_кр или ω < а и всякое понижение давления р₂ передается вдоль сопла в направлении, обратном движению потока, со скоростью а-ω.

Если же р₂ снизится до p_кр, то дальнейшее понижение его уже не сможет распространяться вдоль сопла, поскольку скорость его распространения навстречу потоку снизится до нуля (а-ω_кр= 0). Поэтому расход газа не изменится в выходном сечении, т.е. скорость истечения останется постоянной и равной ω_кр.