ПОТЕРИ НАПОРА ПО ДЛИНЕ ПРИ ТУРБУЛЕНТНОМ УСТАНОВИВШЕМСЯ РАВНОМЕРНОМ ДВИЖЕНИИ ЖИДКОСТИ
И.Никурадзе были проведены опыты по исследованию влияния шероховатости поверхности труб и числа Рейнольдса на потери напора по длине и на коэффициент гидравлического трения, т.е.  . Опыты осуществлялись на гидравлическом стенде с круглыми трубами с искусственной однородной шероховатостью. Искусственная шероховатость создавалась путем наклеивания на внутреннюю поверхность труб песчинок одинакового размера. Относительные шероховатости в опытах были в пределах
. Опыты осуществлялись на гидравлическом стенде с круглыми трубами с искусственной однородной шероховатостью. Искусственная шероховатость создавалась путем наклеивания на внутреннюю поверхность труб песчинок одинакового размера. Относительные шероховатости в опытах были в пределах 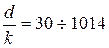 . Эксперименты проводились как при ламинарном, так и при турбулентном режиме движения жидкости. Число Рейнольдса в экспериментах находилось в диапазоне
. Эксперименты проводились как при ламинарном, так и при турбулентном режиме движения жидкости. Число Рейнольдса в экспериментах находилось в диапазоне 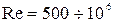 . В трубах с разной относительной шероховатостью определялись потери напора по длине
. В трубах с разной относительной шероховатостью определялись потери напора по длине 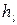 , при различных расходах. Коэффициенты гидравлического трения
, при различных расходах. Коэффициенты гидравлического трения  вычислялись по формуле
вычислялись по формуле
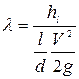 .
.
По средней скорости V 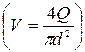 находилось число Рейнольдса
находилось число Рейнольдса 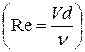 . Результаты опытов были представлены в виде графиков, которые имели функциональную зависимость
. Результаты опытов были представлены в виде графиков, которые имели функциональную зависимость  с учетом относительной шероховатости в виде
с учетом относительной шероховатости в виде  (рис. 4.13). Величины
(рис. 4.13). Величины  и Re - безразмерные.
и Re - безразмерные.

Рис. 4.13. График Никурадзе
На графике по оси ординат были отложены значения 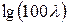 , а по оси абсцисс - величины
, а по оси абсцисс - величины  . График позволил весьма наглядно показать влияние шероховатости трубы и числа Рейнольдса на коэффициент гидравлического трения и, соответственно, на потери напора по длине трубы.
. График позволил весьма наглядно показать влияние шероховатости трубы и числа Рейнольдса на коэффициент гидравлического трения и, соответственно, на потери напора по длине трубы.
На графике Никурадзе (см. рис. 4.13) можно выделить следующие характерные зоны ламинарного, неустойчивого и турбулентного режимов движения.
Ламинарная зона. В этой зоне полученные экспериментально величины  при разных относительных шероховатостях
при разных относительных шероховатостях  легли на прямую I-I в левой стороне графика при значениях Re<2300 (
легли на прямую I-I в левой стороне графика при значениях Re<2300 (  =3,36), что соответствует ламинарному режиму движения. Таким образом, в данной зоне
=3,36), что соответствует ламинарному режиму движения. Таким образом, в данной зоне  не зависит от шероховатости труб, а зависит только от числа Re. Прямая линия I-I соответствует функции
не зависит от шероховатости труб, а зависит только от числа Re. Прямая линия I-I соответствует функции  , полученной теоретическим путем (см. п. 4.5, формула (4.68)).
, полученной теоретическим путем (см. п. 4.5, формула (4.68)).
Переходная (неустойчивая) зона. Эта зона соответствует переходу ламинарного движения в турбулентное и наоборот. На графике зона находится между линиями I-I и II-II при значениях числа Рейнольдса  (
(  ). Значение коэффициента
). Значение коэффициента  в этой зоне не зависит от шероховатости,
в этой зоне не зависит от шероховатости,  .
.
Турбулентная зона. В турбулентной зоне имеется семейство кривых в зависимости от относительной шероховатости в виде  . Начало кривых находится по линии II-II. Турбулентная зона разбивается на три области: гладкого сопротивления (гидравлически гладкие трубы), доквадратичного и квадратичного сопротивления (гидравлически шероховатые трубы).
. Начало кривых находится по линии II-II. Турбулентная зона разбивается на три области: гладкого сопротивления (гидравлически гладкие трубы), доквадратичного и квадратичного сопротивления (гидравлически шероховатые трубы).
Область гладкого сопротивления представляется на графике линией II-II при разных значениях  и числах Re. В этой области
и числах Re. В этой области  не зависит от шероховатости а зависит только от числа Re,
не зависит от шероховатости а зависит только от числа Re,  . Шероховатость внутренней поверхности труб не оказывает сопротивления движению жидкости при турбулентном режиме. Такие трубы называют гидравлически гладкими. В пределах этой области потери напора можно выразить зависимостью
. Шероховатость внутренней поверхности труб не оказывает сопротивления движению жидкости при турбулентном режиме. Такие трубы называют гидравлически гладкими. В пределах этой области потери напора можно выразить зависимостью
 . (4.91)
. (4.91)
Область доквадратичного сопротивления находится между линиями II-II и III-III. В этой области имеется ряд кривых, отражающих разную степень шероховатости. Коэффициент  зависит одновременно от двух параметров - числа Re и
зависит одновременно от двух параметров - числа Re и  :
:  . Потери напора в этой области
. Потери напора в этой области
 . (4.92)
. (4.92)
Область квадратичного сопротивления располагается правее линии III-III. Линии, соответствующие определенным значениям  , практически параллельны друг другу. Потери напора по длине в этом случае
, практически параллельны друг другу. Потери напора по длине в этом случае
 . (4.93)
. (4.93)
В этой области на 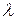 не влияет число Рейнольдса. а только
не влияет число Рейнольдса. а только 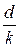 :
:  .
.
Так как потери напора зависят от квадрата скорости, то эту область называют областью квадратичного сопротивления, а трубы являются гидравлически шероховатыми.
Особенности сопротивлений при турбулентном движении объясняются образованием пограничного слоя с вязкостным подслоем. При достаточно малых числах Re толщина вязкостного подслоя  больше высоты выступов (бугорков) шероховатости:
больше высоты выступов (бугорков) шероховатости: 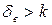 , тогда шероховатость будет находиться внутри пограничного слоя. Сопротивление в этом случае не зависит от шероховатости - сопротивление гладкое. При увеличении числа Рейнольдса, т.е. при повышении скорости в трубе, толщина
, тогда шероховатость будет находиться внутри пограничного слоя. Сопротивление в этом случае не зависит от шероховатости - сопротивление гладкое. При увеличении числа Рейнольдса, т.е. при повышении скорости в трубе, толщина  уменьшается в результате пульсации скоростей в пограничном слое и вне его. Вязкостный подслой будет находиться в пределах выступов шероховатости
уменьшается в результате пульсации скоростей в пограничном слое и вне его. Вязкостный подслой будет находиться в пределах выступов шероховатости 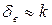 . Сопротивления, имеющиеся в данном случае, - переходные сопротивления.
. Сопротивления, имеющиеся в данном случае, - переходные сопротивления.
В случае больших скоростей и, соответственно, чисел Re вязкостный подслой практически исчезает, а в пограничном слое возникают малые вихри в результате отрыва частичек жидкости от выступов (бугорков). Шероховатость поверхности труб  влияет на сопротивление движению, и такое сопротивление является квадратичным сопротивлением.
влияет на сопротивление движению, и такое сопротивление является квадратичным сопротивлением.
Следует отметить, что Никурадзе проводил исследования с трубами с однородной искусственной шероховатостью. На практике трубы, используемые в обычных производственных условиях, имеют естественную шероховатость. Для выяснения влияния естественной шероховатости были проведены многочисленные экспериментальные исследования как отечественными, так и зарубежными учеными.
Наиболее обстоятельные исследования с техническими трубами были проведены Колбруком (1938) и Г. Муриным (1948).
На рис. 4.14 приведен график Колбрука, показывающий функциональную зависимость  от относительной эквивалентной шероховатости
от относительной эквивалентной шероховатости 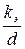 . Используя график, для турбулентного движения можно определить коэффициент
. Используя график, для турбулентного движения можно определить коэффициент 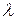 . На основании результатов исследования были получены различные формулы для вычисления
. На основании результатов исследования были получены различные формулы для вычисления 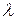 в областях турбулентного движения жидкости.
в областях турбулентного движения жидкости.

Рис. 4.14. График Колбрука
Дата добавления: 2015-12-29; просмотров: 700;
