ПОТЕРИ НАПОРА ПО ДЛИНЕ ПРИ РАВНОМЕРНОМ УСТАНОВИВШЕМСЯ ДВИЖЕНИИ ЖИДКОСТИ

При равномерном установившемся движении жидкости в трубе средняя скорость и распределение скоростей по длине остаются неизменными. Следовательно, при определении потерь напора по длине можно использовать основное уравнение равномерного движения как при ламинарном, так и турбулентном движении в круглой трубе, выразив касательное напряжение на стенке формулой

.

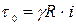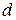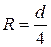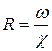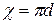Для круглой трубы диаметром гидравлический радиус ( , площадь живого сечения , смоченный периметр ). Так как гидравлический уклон 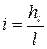, то касательные напряжения на внутренней поверхности трубы при движении вязкой жидкости будут равны

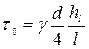(4.25)

Опытами было установлено, что сила сопротивления 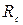при обтекании твердого тела вязкой жидкостью при установившемся движении зависит от определенных параметров и эти сопротивления можно представить в виде следующей функциональной зависимости:

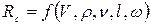, (4.26)

где V - скорость набегающего потока жидкости; 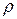- плотность жидкости; 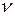- кинематическая вязкость; 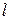- характерный линейный размер тела; 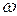- наибольшее сечение тела, которое перпендикулярно вектору скорости 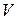набегающего потока.

На основании анализов опытов и использования теории размерностей сила сопротивления может быть представлена следующей формулой:

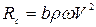, (4.27)

где b - некоторый безразмерный коэффициент пропорциональности, называемый коэффициентом сопротивления; 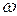- площадь тела.

Полагаем, что касательные напряжения, возникающие на поверхности тела, равны

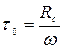. (4.28)

Тогда

. (4.29)

Воспользуемся полученной зависимостью для нахождения выражения по определению потерь напора по длине круглой трубы. Считаем, что касательные напряжения на поверхности трубы можно выразить зависимостью (4.29), V - средняя скорость в трубе.

Напишем равенство, используя формулы (4.25) и (4.29):

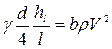. (4.30)

Потери напора по длине определим из равенства

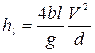. (4.31)

Умножив и разделив на 2 выражение (4.31), получим

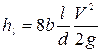. (4.32)

Обозначим 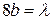, - безразмерный коэффициент, который получил название коэффициента гидравлического трения.

Окончательная форма потерь напора по длине имеет следующий вид:

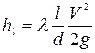. (4.33)

Формулу (4.33) принято называть формулой Вейсбаха-Дарси.

Учитывая уравнение равномерного движения в виде (4.24), коэффициент гидравлического трения можно выразить в виде

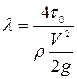, (4-34)

где 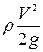- динамическое давление.

Коэффициент пропорционален отношению касательных напряжений на стенке трубы к динамическому давлению, создаваемому потоком жидкости. В общем случае коэффициент гидравлического трения зависит от режима движения (ламинарного или турбулентного). На касательные напряжения на стенке 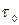трубы влияет шероховатость ее поверхности.

В случае безнапорного движения жидкости в различных руслах (каналы, канализационные и дренажные трубы) формула Вейсбаха-Дарси (4.33) не может быть применена. Для безнапорного установившегося равномерного турбулентного движения жидкости гидравлические потери по длине потока вычисляются по формуле Шези.

Для вывода формулы Шези используем зависимости (4.23) и (4.29) для 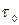. Напишем равенство

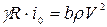. (4.35)

Средняя скорость в русле из (4.35)

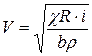. (4.36)

Или, учитывая, что ,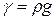

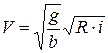(4.37)

В полученной зависимости обозначаем 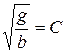. Коэффициент С получил название коэффициента Шези.

Средняя скорость при равномерном движении жидкости в русле

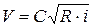. (4.38)

Расход в русле площадью живого сечения 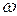составляет

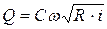. (4.39)

Зависимости (4.38) и (4.39) называют формулами Шези.

Формулы Шези могут служить для определения средней скорости в случае установившегося равномерного движения жидкости не только в безнапорных руслах, но и в трубах.

Следует учитывать, что формула применима только в случае квадратичной области сопротивления. Значения коэффициента С определяются по эмпирическим формулам, полученным в результате опытов с открытыми руслами и трубами.

Для удобства использования формул Шези вводят следующие обозначения:

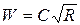- модуль скорости, м/с;

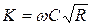- модуль расхода, м/с. (4.40)

С учетом выражений модулей скорости и расхода формулы Шези принимают вид:

;

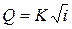. (4.41)

Гидравлические потери напора по длине трубы получим из формулы Шези, где :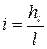

; (4.42)

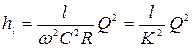. (4.43)

Удобно формулу потерь напора по длине для квадратичной области сопротивлений выразить через расход:

; (4.44)

. (4.45)

Параметр А получил название «удельное сопротивление».

Формула (4.44) называется трубопроводной формулой.

Трубопроводную формулу можно получить, применив формулу Вейсбаха-Дарси (4.33), выразив скорость через расход, - :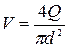

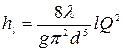, (4-46)

где

.

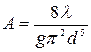Используя зависимости (4.44), (4.45) и (4.46), можно определить связь коэффициента Шези С и коэффициента гидравлического трения , приняв полное наполнение жидкостью трубы , :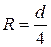

; ,

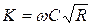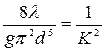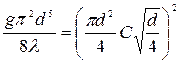откуда

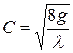. (4.47)