Расчет всасывающей трубы центробежного насоса

Всасывающая труба центробежного насоса представляет собой водовод от места забора воды (водоем) до насоса (рис. 5.1). На входе в насос в сечении 2-2 установлен вакуумметр.

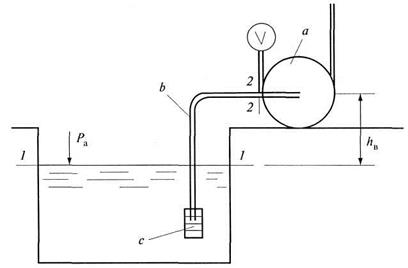
Рис. 5.1. К расчету всасывающей трубы насоса:

а - центробежный насос; b - всасывающий трубопровод;

с - клапан с решеткой; - расстояние от уровня воды в водоеме до оси насоса

При заданном расходе Q среднюю скорость потока в трубе V обычно принимают в пределах 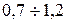м/с. Задавшись скоростью, можно определить площадь сечения всасывающей трубы:

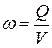
При известном расходе Q во всасывающем трубопроводе диаметр этого трубопровода будет

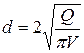. (5.4)

Составим уравнение Бернулли для сечений 1-1 и 2-2 относительно плоскости сравнения 0-0, совпадающей с уровнем воды в водоеме и сечением 1-1, где давление 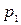равно атмосферному , а скорость 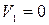. Сечение 2-2 принимаем на всасывающем трубопроводе на входе в насос:

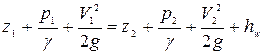, (5.5)

где 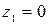; 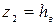- высота всасывания, т.е. расстояние по вертикали от плоскости 1-1 до оси насоса; 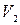- скорость на входе в насос и в самой всасывающей трубе; 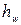- суммарные потери напора в трубе.

Давление в сечении 2-2 принимаем равным абсолютному, т.е. .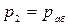

Суммарные гидравлические потери в трубопроводе

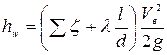, (5.6)

где 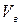- средняя скорость потока трубе, 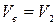; 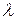- коэффициент гидравлического трения; 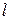, d - длина и диаметр трубопровода соответственно; 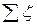- сумма коэффициентов местных сопротивлений трубопровода.

Абсолютное давление на входе в насос 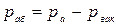( 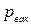- вакуумметрическое давление на входе в насос). Уравнение Бернулли можно записать как

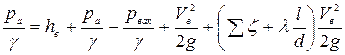(5.7)

или

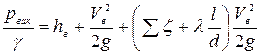. (5.8)

Обозначим 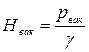, 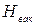- вакуумметрический напор.

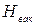применительно к лопастному насосу называется вакуумметрической высотой всасывания. 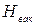зависит от конструктивных особенностей насоса и расхода, .

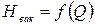Из уравнения (5.8) можно определить высоту всасывания насоса:

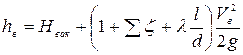. (5.9)

Таким образом, высота всасывания 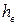насоса зависит от вакуумметрической высоты всасывания насоса и гидравлических потерь во всасывающем трубопроводе.

Вакуумметрическая высота всасывания 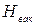определяется по кавитационной характеристике насоса.

Пример 5.1

Вода ( 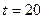°С) из водонапорной башни подается в приемный резервуар по новому трубопроводу из сварных стальных труб диаметром d длиной 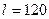м. На трубопроводе имеется задвижка, обратный клапан.

Определить диаметр трубопровода при условии открытия задвижки на 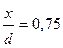и обеспечении расхода 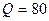л/с. Разность уровней воды в башне и резервуаре считать постоянной и равной 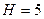м (рис. 5.2).

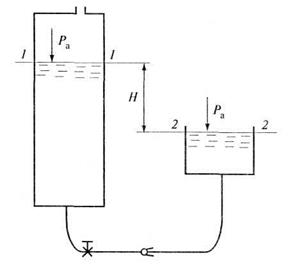
Рис. 5.2. К примеру 5.1

Составив уравнение Бернулли для сечений 1-1 и 2-2, проведя плоскость сравнения по сечению 2-2, получим 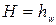, где - гидравлические потери в трубопроводе:

.

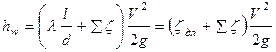Средняя скорость в трубопроводе

.

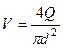Коэффициент гидравлического трения находим по формуле 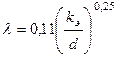для квадратичной области сопротивления.

Шероховатость сварных стальных труб 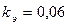мм (см. табл. 3.1).

Сумма коэффициентов местных сопротивлений

,

где 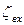- коэффициент сопротивлений на входе в трубу из резервуара; 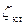- сопротивление обратного клапана; 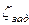- сопротивление задвижки; 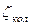- сопротивление колена; 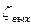- сопротивление на выходе из трубы в резервуар.

По табл. П1.4 приложения находим значения :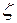

; ; ; .

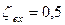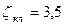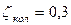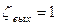В табл. 4.2 находим 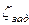при открытии на 0,75: .

.

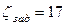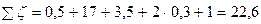Коэффициент сопротивления системы

.

Задаемся разными диаметрами d, определим 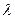, среднюю скорость, 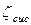и потери напора .

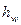Вычисления сводим в табл. 5.1.

Таблица 5.1

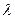
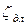
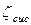
№ п/п	d, м				V, м/с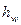
	0,2	0,0145	8,7	31,3	2,55	11,37
	0,225	0,0141	7,52	30,12	2,01	6,82
	0,25	0,0137	6,57	29,17	1,63	4,43
	0,275	0,0134	5,83	28,43	1,35	2,64

Строим график 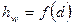(рис. 5.3). На графике по вертикальной оси откладываем 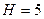м, проводим горизонтальную линию до пересечения с кривой .

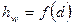Сносим полученную в результате пересечения точку на горизонтальную ось d, получаем м. Согласно ГОСТ на стальные трубы ближайший внутренний диаметр (условный проход) 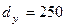мм. Принимае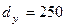м мм.

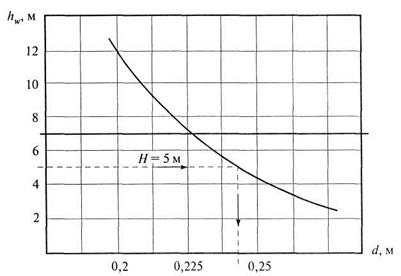
Рис. 5.3. К примеру 5.1