Расчет простого трубопровода.

3). Задано Н, Q определить d=?

Расчет простого трубопровода.

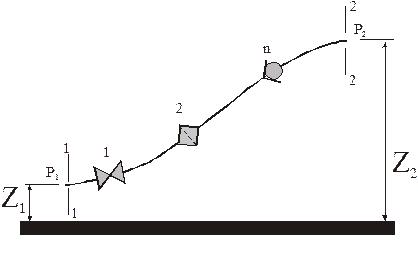
Для перемещения (транспорта) жидкостей и газов применяют трубопроводы, изготовленные из разных материалов: стали, чугуна, бетона, пласт­массы, асбестоцемента и др. Трубопроводы бывают напорные и без­напорные, короткие и длинные, простые и сложные.

Пропускная способность напорных трубопроводов существенно зависит от потерь напора по длине и в местных сопротивлениях (стыках, арматуре и т. п.).

Трубопроводы малой длины и с большим числом местных со­противлений, потери напора в которых превышают 10% потерь на­пора но длине (коммуникации насосных станций, лабораторий, маслопроводы и др.), называют короткими.

К длинным относят трубопроводы большой протяженности, в которых потери напора на преодоление местных сопротивлений не­значительны (не более 10% потерь напора по длине).

Трубопроводы из труб одного или нескольких диаметров без ответвлений и без раздачи расхода по пути движения жидкости на­зывают простыми.

Трубопроводы из сети труб различного диаметра с магистраль­ными линиями и с ответвлениями (тупиковые, кольцевые) называют сложными.

ОСНОВНЫЕ ФОРМУЛЫ ДЛЯ ГИДРАВЛИЧЕСКОГО РАСЧЕТА ТРУБОПРОВОДОВ

Гидравлический расчет трубопроводов позволяет решать три основные задачи:

1) определять необходимый напор для пропуска известного рас­хода воды при заданном диаметре труб;

2) определять пропускную способность труб заданного диаметра при известных потерях напора;

3) определять сечение трубопроводов при заданных расходах воды и потерях напора.

Потери напора в трубопроводе слагаются из потерь на трение по длине и потерь на преодоление местных сопротивлений, т. е.

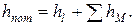(1.104)

Потери напора по длине трубопроводов опреде­ляют по формуле Дарси—Вейсбаха:

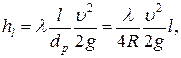
где λ — коэффициент сопротивления трения по длине l;

d_p — расчетный внутренний диаметр труб, м;

υ — средняя скорость движения жидкости, м/с;

R — гидравлический радиус.

Если для круглой трубы определить скорость движения жид­кости

(1.105)

то потери напора по длине можно вычислить по формуле

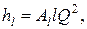(1.1.06)

где 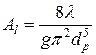- удельное сопротивление, т. е. сопротивление 1 м трубопровода.

Сопротивление по всей длине l трубопровода составит 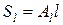и тогда

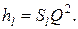(1.107)

Потери напора на единицу длины трубопровода называют гид­равлическим уклоном i т. е.

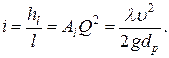(1.108)

Коэффициент сопротивления λ при движении воды в новых и бывших в эксплуатации трубопроводах из различных материалов определяют по зависимостям, полученным во ВНИИ ВОДГЕО д-ром техн. наук Ф. А. Шевелевым:

для новых стальных труб

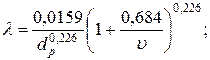
для стальных чугунных труб, бывших в эксплуатации

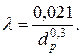
При гидравлических расчетах водопроводных труб удельное сопротивление можно подсчитать по формуле, составленной с учетом увеличения коэффициента λ вследствие возрастания шероховато­сти стенок труб во время их эксплуатации в результате коррозии или образования отложений:

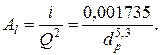(1.109)

Эта формула справедлива при скорости движения воды υ ≥ 1,2 м/с. При меньших скоростях в значения удельных сопротивле­ний вводится поправочный коэффициент К_п на неквадратичность зависимости потерь напора от средней скорости движения жидкости. Тогда формулы (1.106) и (1.107) приобретают такой вид:

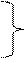
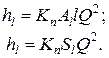(1.110)

Значения поправочного коэффициента К_n изменяются от 1 до 1,4 при изменении скорости от 1,2 до 0,2 м/с. Поправочный коэффи­циент определяют по формуле

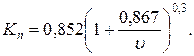
Потери напора на преодоление местных сопротивле­ний определяют по формуле

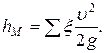(1.111)

По аналогии с формулой (1.106) можно записать

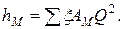
При расчетах трубопроводов местные потери можно выразить в виде потерь напора на трение по эквивалентной длине. При этом h_M = h_MЭ т. е. 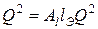или , откуда

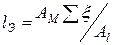(1.112)

Так как d=const, то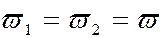

Принимаем режим течения в трубопроводе - стационарным. Течение можно описать уравнением Бернулли.

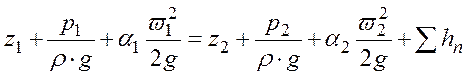
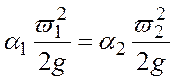
Следовательно:

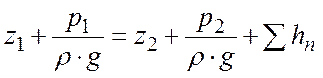
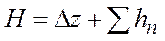
Обобщая полученные зависимости для ламинарного и турбулентного режимов можно записать:

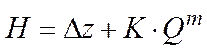
Графическое представление данной зависимости:

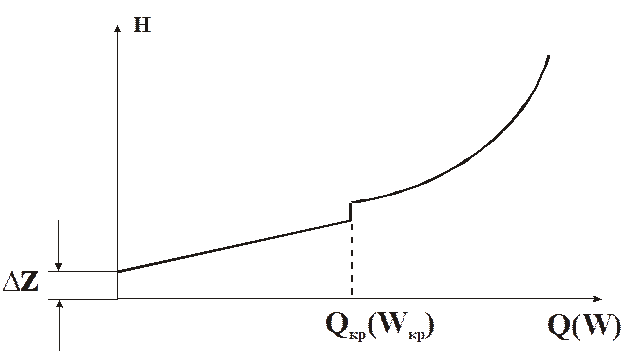
Для ламинарного m=1:

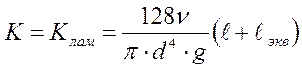
Для турбулентного m=2: