ЦАП прямого цифрового синтеза

ЦАП часто используются для синтеза сигналов специальной формы – синусоидальной, пилообразной, прямоугольной. Кроме этого, в коммуникационных схемах необходимо синтезировать сигналы множества частот с высокой стабильностью и точностью на одном или большем количестве опорных частот. Ранее для этого применялось переключение и смешивание частотных сигналов от группы кварцевых генераторов. Другие методы предусматривали использование цепей фазовой автоподстройки частоты (ФАПЧ).

В связи с широким распространением цифровых методов в настоящее время получил метод прямого цифрового синтеза (ПЦС). Метод ПЦС можно рассмотреть на примере системы прямого цифрового синтеза (рис.28.15).

Рис.28.15. Функциональная схема системы прямого цифрового синтеза

В этой упрощенной схеме стабильный генератор тактового сигнала управляет с помощью адресного счетчика программируемым ПЗУ, который хранит один или более целое число циклов синусоидального сигнала (или другого сигнала произвольной формы). Для уменьшения необходимого объема ППЗУ зачастую в него записывается информация только о четверти периода синусоидального сигнала. По мере того, как адресный счетчик проходит через каждую ячейку памяти, соответствующая цифровая амплитуда сигнала из каждой ячейки подается на ЦАП, который, в свою очередь, воспроизводит аналоговый выходной сигнал.

В связи с дискретной природой ПЦС методу присущи погрешности, характерные для АЦП: шум квантования, наложение спектра, для такого ЦАП на выходе необходим фильтр низких частот. Основной проблемой этой простой ПЦС-системы состоит в том, что выходная частота может быть изменена только путем изменения частоты задающего генератора или посредством перепрограммирования ППЗУ, что делает систему недостаточно гибкой.

На практике ПЦС-системы осуществляют эту функцию более гибким и эффективным способом, используя цифровую схему, называемую генератором с цифровым управлением. Функциональная схема такой системы представлена на рис. 28.16.

Содержимое сумматора фазы обновляется однократно за каждый тактовый цикл. Каждый раз при обновлении сумматора фазы цифровое число М, сохраненное в регистре приращения фазы, добавляется к числу в сумматоре фазы. Если сумматор является 32-разрядным, для полного цикла обновления сумматора фазы требуется 2³² тактовых циклов, после чего цикл повторяется.

Усеченное значение выходного сигнала сумматора фазы служит адресом таблицы задания синуса (или косинуса). Таблица поиска содержит информацию, соответствующую амплитуде для одного полного цикла синусоидального сигнала.

Рис.28.16. ПЦС ЦАП, использующий генератор с цифровым управлением

Для n-разрядного сумматора фазы (в большинстве ПЦС-систем значение n лежит в диапазоне от 24 до 32) существует 2ⁿ значений фазы. Число М в регистре приращения фазы представляет собой величину, на которую текущее значение фазы увеличивается в каждом тактовом цикле. Если f_С – частота синхронизации, то выходная частота синусоидального сигнала равна

f₀ = М f_С / 2ⁿ.

Разрешающая способность системы по частоте равна f_С / 2ⁿ. При n=32 разрешающая способность больше, чем один к четырем миллиардам. В реальной ПЦС-системе не все разряды от сумматора фазы используются для выбора значений из таблицы, оставляются только первые 12-16 старших разрядов, тогда как младшие разряды игнорируются. Это уменьшает размер таблицы и не ухудшает разрешающую способность по частоте.

Описанная ПЦС-система представляет собой гибкое решение с высокой разрешающей способностью. Частота может быть мгновенно изменена без искажения фазы простым изменением содержимого М-регистра.

В качестве примера ПЦС-системы можно привести микросхему AD9850 фирмы Analog Device, содержащую 32-разрядный сумматор фазы и 10-ти разрядный ЦАП. Загрузка приращений фазы осуществляется по 8-ми разрядной шине данных побайтно в четыре входных регистра. Память содержит таблицу синусов. Максимально допустимая частота составляет 125 МГц. При этом разрешение по частоте составляет 0,0291 Гц.

Параметры ЦАП

В настоящее время ассортимент выпускаемых микросхем ЦАП довольно широк. Поскольку все они обладают различными характеристиками, необходимо понимать физический смысл параметров ЦАП, приводимых в технической документации и справочниках.

Статические параметры ЦАП. Допустим, на входы ЦАП подается двоичный код, значения которого меняются от минимального до максимального с шагом, равным 1. Этот входной код преобразуется в дискретные значения выходной аналоговой величины. Совокупностью значений выходного сигнала ЦАП U_ВЫХ в зависимости от входного кода D называется статической характеристикой преобразования.

Рис.28.17. ЦАП прямого цифрового синтеза AD9850

В отсутствие аппаратных погрешностей средние точки ступенек расположены на идеальной прямой 1 (рис. 28.18), которой соответствует идеальная характеристика преобразования. Реальная характеристика преобразования может существенно отличаться от идеальной размерами и формой ступенек, а также расположением на плоскости координат. Точность определяется отклонением действительной выходной аналоговой величины от ее теоретического значения. На точность ЦАП влияют значения основных параметров и температурные дрейфы: эталонного источника, суммирующего усилителя, резистивной схемы и аналоговых ключей. Для количественного описания этих различий существует целый ряд параметров.

1. Разрядность – число символов кода, необходимое для того, чтобы в выбранной системе счисления (как правило, в двоичной) выразить номинальное число квантов.

Рис. 28.18. Статическая характеристика преобразования ЦАП

2. Разрешающая способность – приращение U_ВЫХ при преобразовании смежных значений D_i, т.е. отличающихся на единицу МЗР. Это приращение является шагом квантования. Для двоичных кодов преобразования номинальное значение шага квантования h= U_ПШ / 2N-1, где U_ПШ – номинальное максимальное выходное напряжение ЦАП (напряжение полной шкалы), N – разрядность ЦАП. Чем больше разрядность преобразователя, тем выше его разрешающая способность.

3. Погрешность полной шкалы – относительная разность между реальным и идеальным значениями предела шкалы преобразования при отсутствии смещения нуля.

δ_ПШ = (ε_ПШ / U_ПШ) 100%.

Погрешность полной шкалы является мультипликативной составляющей полной погрешности. Иногда указывается соответствующим числом единиц МЗР.

Рис. 28.19. Линейная погрешность шкалы на единицу МЗР

4. Погрешность смещения нуля – значение U_ВЫХ, когда входной код ЦАП равен нулю. Является аддитивной составляющей полной погрешности. Обычно указывается в милливольтах или в процентах от полной шкалы:

δ_СМ = (ε_СМ / U_ПШ) 100%.

Рис. 28.20. Передаточная характеристика ЦАП со сдвигом нуля на 0.5. МЗР

5. Нелинейность – максимальное отклонение реальной характеристики преобразования U_ВЫХ (D) от оптимальной. Оптимальная характеристика находится эмпирически так, чтобы минимизировать значение погрешности нелинейности. Нелинейность обычно определяется в относительных единицах, но в справочных данных приводится также и в единицах МЗР. Для характеристики, приведенной на рис. 28.21:

δ_Н = (ε_Н / U_ПШ) 100%.

Дифференциальная нелинейность – максимальное изменение (с учетом знака) отклонения реальной характеристики преобразования U_ВЫХ (D) от оптимальной при переходе от одного значения входного кода к другому смежному значению. Обычно определяется в относительных единицах или в ЕМР. Для характеристики, приведенной на рис.28.21:

δ_ДН = ((ε_i +(ε_i+1) / U_ПШ) 100%.

Рис.28.21. Передаточная характеристика ЦАП с нелинейностью ±0.5.МЗР

6. Монотонность характеристики преобразования – возрастание (уменьшение) выходного напряжения ЦАП U_ВЫХ (D) при возрастании (уменьшении) входного кода D. Если дифференциальная нелинейность больше относительного шага квантования h/U_ПШ, то характеристика преобразователя немонотонна.

Рис. 28.22. Немонотонная передаточная характеристика ЦАП (нелинейность должна быть больше ± 0.5 МЗР)

7. Температурная нестабильность ЦАП характеризуется температурными коэффициентами погрешности полной шкалы и погрешности смещения нуля.

8. Диапазон изменения напряжения (U) или тока (I) – полная шкала изменения напряжения от 0 до U_{ВЫХ МАКС} или тока от 0 до I_{ВЫХ МАКС}.

9. Полное выходное сопротивление ЦАП Z_ВЫХ – определяется со стороны выходных зажимов. Оно зависит в основном от выходного сопротивления суммирующего усилителя и имеет порядок сотен Ом.

Погрешности полной шкалы и смещения нуля могут быть устранены калибровкой (подстройкой). Погрешности нелинейности простыми средствами устранить нельзя.

Динамические параметры ЦАП. Динамические параметры ЦАП определяются по изменению выходного сигнала при скачкообразном изменении входного кода, обычно от величины "все нули" до "все единицы" (рис. 28.23).

Рис.28.23. Переходная характеристика ЦАП

1. Время установления, t_УСТ – интервал времени от момента изменения входного кода (на рис. 28.23 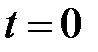) до момента, когда в последний раз выполняется равенство

|U_ВЫХ – U_ПШ| = d / 2.

2. Скорость нарастания – максимальная скорость изменения U_ВЫХ(t) во время переходного процесса. Определяется как отношение приращения ΔU_ВЫХ ко времени Δ 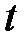, за которое произошло это приращение. Обычно указывается в технических характеристиках ЦАП с выходным сигналом в виде напряжения. У ЦАП с токовым выходом этот параметр в большой степени зависит от типа выходного ОУ.

3. Частота обновления – максимальная частота, с которой может происходить смена содержимого входных регистров ЦАП.

Применение ЦАП в различной радиоэлектронной аппаратуре, прежде всего, непосредственно связано со скоростью преобразования, значение которой определяется временем установления. Требуемые значения скорости преобразования изменяются в диапазоне от нескольких герц до десятков мегагерц в зависимости от области применения ЦАП. В связи с этим применяют время установления как классификационный параметр для разделения ЦАП на группы среднего, высокого и сверхвысокого быстродействия, характеризуемые соответственно значениями времени установления в пределах 20…1; 1…0,1; 0,1…0,01 мкс.

ГЛАВА 29